Korrelation: Unterschied zwischen den Versionen
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Eine Korrelation bezeichnet den Zusammenhang zwischen zwei oder mehr Variablen. Dieser Zusammenhang kann positiv oder negativ sein. | Eine Korrelation bezeichnet den Zusammenhang zwischen zwei oder mehr Variablen. Dieser Zusammenhang kann positiv oder negativ sein. | ||
[[Datei:Korrelation1.png|400px|link=Ausgelagerte_Bildbeschreibungen# | [[Datei:Korrelation1.png|400px|link=Ausgelagerte_Bildbeschreibungen#Korrelation_1|Ausgelagerte Bildbeschreibung von Korrelation 1]] | ||
<br/>Ausgedrückt wird eine Korrelation mithilfe von Korrelationskoeffizienten (KK). Diese bezeichnen die Enge und Richtung von Zusammenhängen. | <br/>Ausgedrückt wird eine Korrelation mithilfe von Korrelationskoeffizienten (KK). Diese bezeichnen die Enge und Richtung von Zusammenhängen. | ||
| Zeile 19: | Zeile 19: | ||
<br/>Die Stärke des Zusammenhangs wird hierbei durch den Abstand von 0 gekennzeichnet. Normalerweise gelten Korrelationen mit einem Betrag von unter 0,3 als schwach und Korrelationen mit einem Betrag ab 0,5 als stark. | <br/>Die Stärke des Zusammenhangs wird hierbei durch den Abstand von 0 gekennzeichnet. Normalerweise gelten Korrelationen mit einem Betrag von unter 0,3 als schwach und Korrelationen mit einem Betrag ab 0,5 als stark. | ||
In Streudiagrammen gilt grundsätzlich: je mehr die Punktwolke einer Geraden gleicht, desto stärker ist der Zusammenhang – je mehr sie einem Kreis gleicht, desto schwächer ist er. Starke Korrelationen sehen beispielsweise folgendermaßen aus: | In Streudiagrammen gilt grundsätzlich: je mehr die Punktwolke einer Geraden gleicht, desto stärker ist der Zusammenhang – je mehr sie einem Kreis gleicht, desto schwächer ist er. Starke Korrelationen sehen beispielsweise folgendermaßen aus: | ||
<br/>[[Datei:Korrelation2.png|600px]] | <br/>[[Datei:Korrelation2.png|600px|link=Ausgelagerte_Bildbeschreibungen#Korrelation_2|Ausgelagerte Bildbeschreibung von Korrelation 2]] | ||
<br/> | <br/> | ||
'''Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden! ''' | '''Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden! ''' | ||
<br/>Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben: | <br/>Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben: | ||
[[Datei:Korrelation3.png|500px]] | [[Datei:Korrelation3.png|500px|link=Ausgelagerte_Bildbeschreibungen#Korrelation_3|Ausgelagerte Bildbeschreibung von Korrelation 3]] | ||
Mögliche Interpretationen einer Korrelation sind: | Mögliche Interpretationen einer Korrelation sind: | ||
Aktuelle Version vom 2. Dezember 2021, 15:53 Uhr
Eine Korrelation bezeichnet den Zusammenhang zwischen zwei oder mehr Variablen. Dieser Zusammenhang kann positiv oder negativ sein.

Ausgedrückt wird eine Korrelation mithilfe von Korrelationskoeffizienten (KK). Diese bezeichnen die Enge und Richtung von Zusammenhängen.
Es gibt verschiedene Arten von Korrelationskoeffizienten:
- Produkt-Moment-Korrelation (linearer Zusammenhang zweier intervallskalierter Merkmale)
- Rangkorrelation (monotoner Zusammenhang zweier ordinalskalierter Merkmale)
- Kontingenzkoeffizient (atoner Zusammenhang zweier nominalskalierter Merkmale)
- Bei mehr als 2 Merkmalen erhält man multivariate Korrelationskoeffizienten.
Am häufigsten finden sich Produkt-Moment-Korrelationen als Korrelationskoeffizienten. Diese können sowohl im positiven Bereich als auch im negativen Bereich sein. Ein positiver KK bedeutet, dass der Zusammenhang eng ist. Bei zwei betrachteten Ereignissen würde dies bedeuten, dass ein Ereignis häufig dann auftritt, wenn auch ein anderes Ereignis auftritt. Ein negativer KK bei zwei betrachteten Ereignissen bedeutet entsprechend, dass ein Ereignis in der Regel dann auftritt, wenn das andere Ereignis nicht auftritt.
Zur Beschreibung des Korrelationskoeffizienten wird häufig der Buchstabe r genutzt. Der Wert von r liegt immer zwischen -1 und 1.
Bei einem positiven Zusammenhang (d.h. mit höherem Wert der Variable A steigt auch der Wert der Variable B) ist der Wert größer als null, bei einem negativen Zusammenhang (d.h. mit höherem Wert der Variable A sinkt der Wert der Variable B) kleiner als Null und bei keinerlei Zusammenhang der Variablen beträgt r exakt 0.
Die Stärke des Zusammenhangs wird hierbei durch den Abstand von 0 gekennzeichnet. Normalerweise gelten Korrelationen mit einem Betrag von unter 0,3 als schwach und Korrelationen mit einem Betrag ab 0,5 als stark.
In Streudiagrammen gilt grundsätzlich: je mehr die Punktwolke einer Geraden gleicht, desto stärker ist der Zusammenhang – je mehr sie einem Kreis gleicht, desto schwächer ist er. Starke Korrelationen sehen beispielsweise folgendermaßen aus:
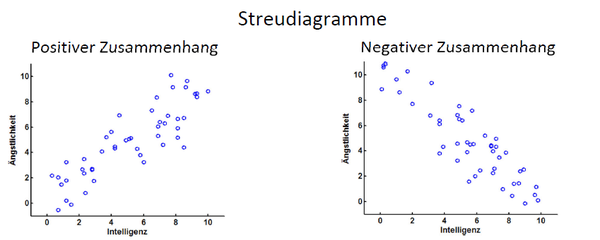
Wichtig: Die Korrelation ist nur eine deskriptive Beziehung zwischen den Variablen, es kann hier keine Aussage über einen Kausalzusammenhang getroffen werden!
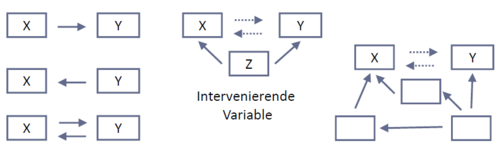
Aus einer Korrelation zwischen zwei Variablen kann nicht etwa geschlossen werden, dass sich Variable X in bestimmter Weise auf Variable Y auswirkt. Eine gemeinsame Veränderung kann unzählige andere Ursachen haben:
Mögliche Interpretationen einer Korrelation sind:
- Koinzidenz (Das gemeinsame Auftreten ist zufällig zustande gekommen.
- X ist ein Teil von Y
- Moderator- oder Mediatoreffekte (eine gemeinsame Drittvariable steuert den Prozess)
- Kausalität
- Umgekehrte Kausalität
Beispiel: In einer Studie wurde herausgefunden, dass Kinder, die mit ihrem rechten Arm über den Kopf an ihr linkes Ohrläppchen fassen können, auch gleichzeitig als schulfähig eingestuft werden können. Das Beherrschen dieser Handlung ist jedoch keine Ursache für die Schulfähigkeit. Eine dahinterliegende Drittvariable (ausreichende körperliche Entwicklung des Kindes) bedingt die Korrelation.