Grundlagen der multiplen linearen Regression

In der psychologischen Forschung wird häufig der Einfluss von mehr als einem Prädiktor auf eine Kriteriumsvariable untersucht. Die multiple lineare Regression (MLR) ist die Methode der Wahl, um aus mehreren Prädiktoren diejenigen auszuwählen, die einen entscheidenden Beitrag zur Vorhersage liefern.

Die MLR ist eine Erweiterung der einfachen linearen Regression. Sie stellt das Kriterium als lineare Funktion von zwei oder mehr Prädiktoren dar und kann mit der folgenden Formel beschrieben werden:

Jeder Messwert y_i kann durch die lineare Kombination der Prädiktorwerte (x_1i, …, x_1k) und einem zufälligen Residuum e_i erklärt werden. Die Regressionskoeffizienten (b₀, b₁, …, b_k) sind nicht bekannt und werden mithilfe der Methode der kleinsten Quadrate aus den Daten geschätzt.

Die Methode der kleinsten Quadrate zur Schätzung der Regressionskoeffizienten, die Voraussetzungen zur Anwendung der MLR und die Berechnung des Bestimmtheitsmaßes sind analog zu der einfachen linearen Regression und können im Text zur einfachen linearen Regression nachvollzogen werden. Anders als bei der einfachen linearen Regression gibt es keine Möglichkeit, die Schätzung der Regressionskoeffizienten bzw. des Bestimmtheitsmaßes zu vereinfachen. Um diese zu bestimmen muss dementsprechend auf Computerprogramme zurückgegriffen werden.

Beispiel

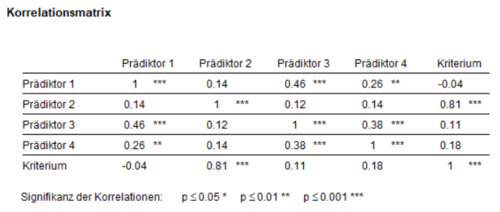
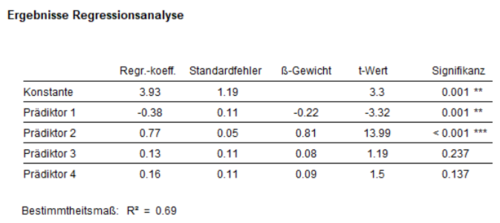
In einer fiktiven Studie wird der Einfluss von vier Prädiktoren auf ein Kriterium untersucht. Um deskriptiv die Zusammenhänge zwischen den Prädiktoren und dem Kriterium und zwischen den Prädiktoren zu berechnen, werden zunächst die bivariaten Korrelationskoeffizienten berechnet. Aus dem signifikanten Korrelationskoeffizienten zwischen Prädiktor 2 und dem Kriterium (r = 0.81) lässt sich z.B. vermuten, dass Prädiktor 2 einen bedeutenden Einfluss auf das Kriterium hat (Abbildung 1). Dies wird in der regressionsanalytischen Betrachtung (Abbildung 2) bestätigt.

kkk

Unter Einbezug aller Prädiktoren ergibt sich für das vorliegende Beispiel die folgende Regressionsgleichung:

Die Signifikanz der einzelnen Regressionskoeffizienten lässt sich mithilfe eines t-Tests feststellen, welcher die Nullhypothese H₀: b_i = 0 (i= 1, …, k) testet. Die t-Werte werden als Quotient aus Regressionskoeffizient und dessen Standardfehler bestimmt und geben Aufschluss darüber, ob die Prädiktoren dieses Modells einen statistisch abgesicherten Einfluss auf das Kriterium haben. In diesem Fall haben sowohl Prädiktor 1 als auch Prädiktor 2 einen signifikanten Einfluss auf das Kriterium. Dass Prädiktor 1 trotz sehr geringer und nichtsignifikanter Korrelation mit dem Kriterium im Regressionsmodell signifikant von 0 verschieden ist, könnte ein Hinweis auf Multikollinearität sein.

Um die Regressionskonstante interpretieren und daraus spezifische Aussagen gewinnen zu können, bietet sich analog zur einfachen linearen Regression die Zentrierung aller Prädiktorvariablen vor der Analyse an. Danach entspricht die geschätzte Regressionskonstante dem erwarteten Wert des Kriteriums bei durchschnittlichen Ausprägungen aller Prädiktoren.

Die Höhe der einzelnen Regressionskoeffizienten ist stark abhängig von dem Wertebereich des jeweiligen Prädiktors und sagt somit nichts über die tatsächliche Stärke des Einflusses eines Prädiktors im Vergleich zu den anderen Prädiktoren aus. Um die Einflüsse der Prädiktoren vergleichbar zu machen, kann auf die Methode der z-Standardisierung zurückgegriffen werden. Bei der z-Standardisierung wird die Differenz aus Messwert und arithmetischen Mittelwert zusätzlich durch die Standardabweichung des jeweiligen Merkmals geteilt. Dadurch erhalten alle Merkmale einen Mittelwert von 0 und eine Standardabweichung von 1. Hierbei werden nicht nur die Prädiktoren, sondern auch das Kriterium z-standardisiert. Die daraus entstehenden Regressionskoeffizienten werden als Beta-Koeffizienten bezeichnet und ermöglichen es, vergleichende Aussagen über den Einfluss der Prädiktoren zu treffen. Im beschriebenen Beispiel zeigt sich durch den Vergleich der Beta-Koeffizienten, dass innerhalb des untersuchten Regressionsmodells Prädiktor 2 den größten Einfluss auf das Kriterium hat (β₂ = 0.81). Die Regressionskonstante beträgt bei einer Regressionsanalyse mit z-standardisierten Variablen stets 0, da der Mittelwert aller Variablen 0 beträgt. Die Regressionsgerade verläuft damit durch den Koordinatenursprung. Bei verletzter Homoskedastizitätsvoraussetzung sollte eine Regression mit robusten Standardfehlern berechnet werden (vgl. einfache lineare Regression).

kkk Im Video wird die multiple lineare Regression näher erläutert.

kkk In der interaktiven Simulation kann die Entstehung unterschiedlicher Regressionskoeffizienten und die Überprüfung der Voraussetzungen anhand verschiedener Datensätze nachvollzogen werden.

Weiterführende Literatur

Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.

Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.2). Göttingen: Hogrefe.

Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.6). München: Pearson Studium.