Entscheiden: Signaldetektion: Unterschied zwischen den Versionen
Paul (Diskussion | Beiträge) (→Entscheidungskriterium: liberales/konservatives Kriterium Link einfügen p.b.) |
Elisa (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
Dieser Lösungsansatz ist recht intuitiv: Je geringer der "Noise" und je deutlicher das Signal, desto akkurater fällt die Entscheidung aus. Dies ist das Prinzip der [http://de.wikipedia.org/wiki/Varianzanalyse#Grundidee Varianzanalyse]. | Dieser Lösungsansatz ist recht intuitiv: Je geringer der "Noise" und je deutlicher das Signal, desto akkurater fällt die Entscheidung aus. Dies ist das Prinzip der [http://de.wikipedia.org/wiki/Varianzanalyse#Grundidee Varianzanalyse]. | ||
Das Rauschen (Noise) entspricht dabei der [[Varianz]] innerhalb der "Gruppen" (Gruppe 1 umfasst alle Messungen, bei denen das Signal, z.B. eine Depression, nicht anwesend war – Gruppe 2 die Messungen, bei denen das Signal da war). Minimiert man das Rauschen, werden die Normalverteilungen schmaler und der Überschneidungsbereich somit automatisch kleiner: | Das Rauschen (Noise) entspricht dabei der [[Varianz]] innerhalb der "Gruppen" (Gruppe 1 umfasst alle Messungen, bei denen das Signal, z.B. eine Depression, nicht anwesend war – Gruppe 2 die Messungen, bei denen das Signal da war). Minimiert man das Rauschen, werden die Normalverteilungen schmaler und der Überschneidungsbereich somit automatisch kleiner: | ||
<br/> [[Datei:Signal2.png|500px]] | <br/> [[Datei:Signal2.png|500px|link=Ausgelagerte_Bildbeschreibungen#Gute_Messung|Ausgelagerte Bildbeschreibung von Gute Messung]] | ||
<br/>Die "Streuung zwischen den Gruppen" entspricht hier dem Abstand der Mittelwerte der einzelnen Gruppen – also wie sehr sich eine durchschnittliche Messung bei anwesendem Signal von einer durchschnittlichen Messung bei abwesendem Signal unterscheidet (je größer diese [http://de.wikipedia.org/wiki/Streuung_%28Statistik%29 Streuung], desto "weiter entfernt" sind die Verteilungen voneinander). Ziel ist es also, die Varianz innerhalb der Gruppen zu minimieren und die Varianz zwischen den Gruppen zu maximieren – denn dann sind die exaktesten Entscheidungen möglich (siehe auch [[Max-Kon-Min-Prinzip]]). | <br/>Die "Streuung zwischen den Gruppen" entspricht hier dem Abstand der Mittelwerte der einzelnen Gruppen – also wie sehr sich eine durchschnittliche Messung bei anwesendem Signal von einer durchschnittlichen Messung bei abwesendem Signal unterscheidet (je größer diese [http://de.wikipedia.org/wiki/Streuung_%28Statistik%29 Streuung], desto "weiter entfernt" sind die Verteilungen voneinander). Ziel ist es also, die Varianz innerhalb der Gruppen zu minimieren und die Varianz zwischen den Gruppen zu maximieren – denn dann sind die exaktesten Entscheidungen möglich (siehe auch [[Max-Kon-Min-Prinzip]]). | ||
''(Diesem Ansatz entspräche es, das Telefon lauter zu stellen und die Dusche etwas schwächer laufen zu lassen.)'' | ''(Diesem Ansatz entspräche es, das Telefon lauter zu stellen und die Dusche etwas schwächer laufen zu lassen.)'' | ||
<br/> | <br/> | ||
== Entscheidungskriterium == | == Entscheidungskriterium == | ||
<br/>Auch durch alle Bemühungen ist es oft nicht möglich, komplett eindeutige Messergebnisse zu erhalten. Deshalb ist es nötig, ein '''Entscheidungskriterium''' festzulegen – also zu bestimmen, ab wann eine falsche Entscheidung unwahrscheinlich genug ist, um eine Annahme zu akzeptieren. | <br/>Auch durch alle Bemühungen ist es oft nicht möglich, komplett eindeutige Messergebnisse zu erhalten. Deshalb ist es nötig, ein '''Entscheidungskriterium''' festzulegen – also zu bestimmen, ab wann eine falsche Entscheidung unwahrscheinlich genug ist, um eine Annahme zu akzeptieren. | ||
In der Statistik wird dies [http://de.wikipedia.org/wiki/Statistische_Signifikanz Alpha-Niveau] genannt und häufig auf 5% angesetzt. Das bedeutet: Wenn die Wahrscheinlichkeit, dass die Messwerte aus der Gruppe 1 stammen, unter 5% liegt, ist es legitim, anzunehmen, dass sie aus Gruppe 2 stammen (also, dass das Signal anwesend war). | In der Statistik wird dies [http://de.wikipedia.org/wiki/Statistische_Signifikanz Alpha-Niveau] genannt und häufig auf 5% angesetzt. Das bedeutet: Wenn die Wahrscheinlichkeit, dass die Messwerte aus der Gruppe 1 stammen, unter 5% liegt, ist es legitim, anzunehmen, dass sie aus Gruppe 2 stammen (also, dass das Signal anwesend war). | ||
<br/>Generell gibt es 4 mögliche Entscheidungen, von denen 2 eine Fehlentscheidung darstellen: | <br/>Generell gibt es 4 mögliche Entscheidungen, von denen 2 eine Fehlentscheidung darstellen: | ||
<br/> | |||
{| class="wikitable" style="text-align:center;" | |||
|- style="font-weight:bold;" | |||
! rowspan="2" colspan="2" | Signal Detection Theory<br />(Tanner & Swets, 1954) | |||
! colspan="2" | Interpretation | |||
|- | |||
| 0 | |||
| X | |||
|- | |||
| rowspan="2" style="font-weight:bold; text-align:left;" | Wahrer <br />Wert | |||
| 0 | |||
| Correct <br />Rejection | |||
| style="color:#fe0000;" | False <br />Alarm | |||
|- | |||
| X | |||
| style="color:#fe0000;" | False <br />Rejection | |||
| Hit | |||
|} | |||
<br/>Obwohl das Signal anwesend war, den Fall der Gruppe 1 zuzuordnen ''(den Anruf nicht zu hören)" wird als '''False Rejection''' bezeichnet. Den umgekehrten Fehler – die Messwerte einer Bedingung, bei denen nur Noise existierte, als Signal zu interpretieren ''(umsonst aus der Dusche zu springen)'' – nennt man '''False Alarm'''. | <br/>Obwohl das Signal anwesend war, den Fall der Gruppe 1 zuzuordnen ''(den Anruf nicht zu hören)" wird als '''False Rejection''' bezeichnet. Den umgekehrten Fehler – die Messwerte einer Bedingung, bei denen nur Noise existierte, als Signal zu interpretieren ''(umsonst aus der Dusche zu springen)'' – nennt man '''False Alarm'''. | ||
Aktuelle Version vom 11. Februar 2022, 14:10 Uhr
Ein zentrales Problem der psychologischen Forschung bildet die Entscheidung zwischen Zufall und begründeter Existenz: ab wann gilt ein gemessenes Signal als tatsächlich vorhanden?
Die Signalentdeckungstheorie beschäftigt sich mit Entscheidungskriterien in eben diesen Problemsituationen.
Sie basiert auf der Annahme, dass alles, was wir wahrnehmen und messen, stets eine Mischung aus dem uns interessierenden Signal und einer Art "Hintergrundrauschen", dem Noise ist. Ziel ist es nun, möglichst akkurat zu unterscheiden zwischen Situationen, in denen nur Noise vorhanden ist und Situationen, in denen zusätzlich zum Noise auch das relevante Signal existiert.
(Zur Illustration: Steht man unter der Dusche, bildet das Geräusch des Wassers das Hintergrundrauschen. Man würde sich nun wünschen, korrekt unterscheiden zu können, wann man zusätzlich zum Rauschen auch noch das Klingeln des Telefons gehört hat. Diese Unterscheidung sollte möglichst akkurat geschehen – einerseits möchte man den möglichen Anruf nicht verpassen, andererseits möchte man aber auch nicht umsonst aus der Dusche gesprungen sein.)
In der Psychologie ergibt sich bei Messungen zumeist eine annähernde Normalverteilung. Das bedeutet: bei der Erhebung diverser anwesender Signale (z.B. dem Vorliegen einer Depression), werden die Ergebnisse der meisten Messungen auch für ein Signal sprechen. Einige Messungen werden jedoch fälschlicherweise auf reinen Noise hinweisen (z.B. eine Person ohne psychische Störung). Andersherum gilt dies ebenso, auch Messungen ohne Signal ergeben teilweise Daten, die wiederrum für ein anwesendes Signal sprechen würden (z.B. eine Person ohne psychische Störung, bei der eine Depression diagnostiziert wird). Das Problem das sich nun stellt, ist es, lediglich anhand der Messergebnisse zu entscheiden, um welche der Situationen es sich handelt: war ein Signal da oder nicht.
(Bezogen auf die Situation in der Dusche, heißt dies: Wenn das Telefon nicht klingelt, hört es sich in den meisten Momenten auch genauso an. In einigen Momenten jedoch, glaubt man, ein klingelndes Telefon zu hören, obwohl dies gar nicht der Fall ist. Und andersherum: Ein Klingeln wird meist auch als eines erkannt – teilweise hört es sich jedoch so an, als sei das nur das Rauschen der Dusche gewesen.)
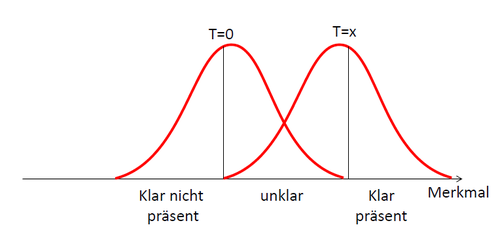
Aus der Abbildung wird das Problem klar ersichtlich: es liegt in der Überschneidung der beiden Verteilungen. Gewisse Messergebnisse können sich sowohl wenn ein Signal anwesend ist ergeben (rechter Graph), als auch wenn es nicht anwesend ist (linker Graph). Aus solchen Ergebnissen auf die Existenz des Signals zu schließen, stellt uns also vor ein Problem.
Gute Messung
Dieser Lösungsansatz ist recht intuitiv: Je geringer der "Noise" und je deutlicher das Signal, desto akkurater fällt die Entscheidung aus. Dies ist das Prinzip der Varianzanalyse.
Das Rauschen (Noise) entspricht dabei der Varianz innerhalb der "Gruppen" (Gruppe 1 umfasst alle Messungen, bei denen das Signal, z.B. eine Depression, nicht anwesend war – Gruppe 2 die Messungen, bei denen das Signal da war). Minimiert man das Rauschen, werden die Normalverteilungen schmaler und der Überschneidungsbereich somit automatisch kleiner:
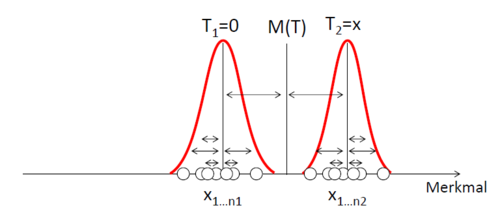
Die "Streuung zwischen den Gruppen" entspricht hier dem Abstand der Mittelwerte der einzelnen Gruppen – also wie sehr sich eine durchschnittliche Messung bei anwesendem Signal von einer durchschnittlichen Messung bei abwesendem Signal unterscheidet (je größer diese Streuung, desto "weiter entfernt" sind die Verteilungen voneinander). Ziel ist es also, die Varianz innerhalb der Gruppen zu minimieren und die Varianz zwischen den Gruppen zu maximieren – denn dann sind die exaktesten Entscheidungen möglich (siehe auch Max-Kon-Min-Prinzip).
(Diesem Ansatz entspräche es, das Telefon lauter zu stellen und die Dusche etwas schwächer laufen zu lassen.)
Entscheidungskriterium
Auch durch alle Bemühungen ist es oft nicht möglich, komplett eindeutige Messergebnisse zu erhalten. Deshalb ist es nötig, ein Entscheidungskriterium festzulegen – also zu bestimmen, ab wann eine falsche Entscheidung unwahrscheinlich genug ist, um eine Annahme zu akzeptieren.
In der Statistik wird dies Alpha-Niveau genannt und häufig auf 5% angesetzt. Das bedeutet: Wenn die Wahrscheinlichkeit, dass die Messwerte aus der Gruppe 1 stammen, unter 5% liegt, ist es legitim, anzunehmen, dass sie aus Gruppe 2 stammen (also, dass das Signal anwesend war).
Generell gibt es 4 mögliche Entscheidungen, von denen 2 eine Fehlentscheidung darstellen:
| Signal Detection Theory (Tanner & Swets, 1954) |
Interpretation | ||
|---|---|---|---|
| 0 | X | ||
| Wahrer Wert |
0 | Correct Rejection |
False Alarm |
| X | False Rejection |
Hit | |
Obwohl das Signal anwesend war, den Fall der Gruppe 1 zuzuordnen (den Anruf nicht zu hören)" wird als False Rejection bezeichnet. Den umgekehrten Fehler – die Messwerte einer Bedingung, bei denen nur Noise existierte, als Signal zu interpretieren (umsonst aus der Dusche zu springen) – nennt man False Alarm.
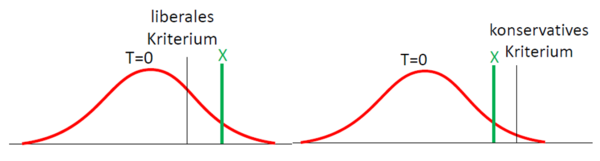
Das Entscheidungskriterium bestimmt nun die Höhe der Wahrscheinlichkeit dieser beiden Fehlerarten. Dabei gilt: Je unwahrscheinlicher die eine, desto wahrscheinlicher die andere (je höher die Wahrscheinlichkeit für einen False Alarm, desto niedriger die Wahrscheinlichkeit für eine False Rejection, und umgekehrt). Häufig hängt das Entscheidungskriterium von den Konsequenzen ab, die die jeweiligen Fehler nach sich ziehen würden.
Ein liberales Kriterium wird angesetzt, wenn es besonders wichtig ist, ein existentes Signal nicht versehentlich zu übersehen.
Beispielsweise wird es bei Bluttests auf tödliche Krankheiten lieber in Kauf genommen, dass der Tests fälschlicherweise ausschlägt, als dass eine tatsächlich erkrankte Person ein negatives Ergebnis erhält und so nicht über ihre Krankheit informiert wird. (In unserem Duschbeispiel entspräche das der Situation eines hoch wichtigen Anrufs, den man auf keinen Fall verpassen möchte.)
Ein konservatives Kriterium wird angesetzt, wenn ein falscher Alarm mit großen Kosten verbunden ist.
Krankenkassen verlangen bei vielen Diagnosen ein sehr eindeutiges Ergebnis über das tatsächliche Vorhandensein der Krankheit. Aus ihrer Sicht wäre es fatal, eine Behandlung zu finanzieren, wenn sich im Nachhinein herausstellt, dass gar keine Krankheit vorlag. (In der Dusche würde man ein konservatives Kriterium ansetzen, wenn man keinen wichtigen Anruf erwartet und wirklich nicht aus der Dusche in die Kälte hüpfen möchte.)
Als Psychologe ist man in verschiedensten Bereichen vom Problem der Signaldetektion betroffen.
Als Forscher spielt Signaldetektion bei der Auswertung vieler Versuchsdaten eine Rolle, denn eine Versuchsperson kann sich z.B. entscheiden, viele Fehler in einem Test zu machen und dafür schnell zu reagieren, oder wenige Fehler zu machen und dafür langsamer zu reagieren. In solchen Fällen kann z.B. von der Reaktionszeit alleine nicht auf die Leistungsfähigkeit einer Person geschlossen werden – vielleicht hatte eine schnelle Person eben auch nur ein liberales Antwortkriterium. Abhilfe für dieses sogennante „Speed-Accuracy-Tradeoff“ Problem kann entweder ein {Index} dienen, welcher Reaktionszeit und Fehlerrate kombiniert oder ein Signalentdeckungstheorietisches Vorgehen, welches die Sensitität der Person (das Signal-Noise-Verhältnis) und das Kriterium der Person errechnet.
Als Forscher spielt Signaldetektion aber auch in der statistischen Auswertung eine Rolle. Die Inferenzstatistik gibt letztlich Auskunft, ob man aufgrund einer experimentellen Manipulation einen Unterschied zwischen Gruppen herstellen konnte oder nicht. In der Regel gilt hier ein recht konservatives Entscheidungskriterium, welches die Forschungscommunity auf 5% Irrtumswahrscheinlichkeit festgelegt hat. Ein Unterschied wird also nur dann als existent akzeptiert, wenn die vorliegenden Daten sehr sicher durch die Manipulation entstanden sind und nur eine 5%ige Wahrscheinlichkeit besteht, dieses Daten zu messen, obwohl kein echter Gruppenunterschied da war.
Als Therapeut spielt Signaldetektion bei der Diagnose psychischer Störungen eine Rolle. Welche und wie viele Kriterien muss eine Person erfüllen, um z.B. als depressiv diagnostiziert zu werden. Das Entscheidungskriterium unterliegt hier sowohl persönlichen Vorlieben, welche vom konservativen Therapeuten bis zum „Viel-hilft-viel“-Therapeuten reichen mag, wirtschaftlichen Interessen des Therapeuten, denn jeder Patient ist auch eine Einnahmequelle, aber auch wirtschaftlichen Interessen des Gesundheitssystems, denn jede Therapie kostet schließlich Geld.