Isomorphismus und Homomorphismus

Homomorphismus
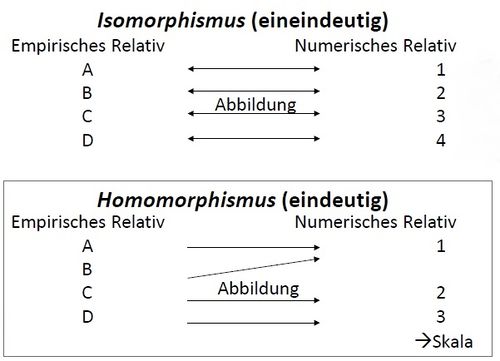
Etwas homomorph abzubilden bedeutet, dass die Daten auf einer Skala die empirische Struktur des untersuchten Phänomens widerspiegeln. Das Phänomen (empirisches Relativ) wird durch zugeordnete Zahlen (numerisches Relativ) so abgebildet, dass die Objektrelationen korrekt repräsentiert sind. (Bortz&Döring, 2006)
Man spricht von einer eindeutigen, strukturerhaltenden Zuordnung.

Peter, Paul und Patrick werden über ihren Lieblingssport befragt. Peter und Paul treiben beide exakt den gleichen Sport und erhalten deshalb beide die gleiche Zahl (1) in der Datenbank. Patrick treibt einen anderen Sport und erhält daher die Zahl (2). Man hat nun also die Datenbank mit den Zahlen 1,1, und 2. Diese Zahlen verhalten sich zueinander genauso, wie die Sportpräferenzen der drei Jungen: 1 und 1 sind gleich, 2 ist anders – Peter und Paul mögen den gleichen Sport, Patrick einen anderen.
Nicht-strukturerhaltend wäre beispielsweise eine willkürliche Zuordnung von Zahlen an die drei Jungen: Peter erhält die 1, Paul die 2 und Patrick die 3. Die Unterschiedlichkeit bzw. Gleichheit ihres Lieblingssports ist nun nicht mehr anhand der Zahlen erkennbar (denn diese sind alle unterschiedlich).

Im Homomorphismus ist es lediglich möglich, ein Objekt eindeutig einer Zahl zuzuordnen. Die Zahl wiederum ist allerdings nicht eindeutig rückführbar auf ein Objekt, da mehrere Objekte die gleiche Zahl erhalten können (siehe obiges Beispiel).


Isomorphismus
Der Isomorphismus ist eine Sonderform des Homomorphismus. Denn isomorphe Abbildungen lassen auch vom empirischen Relativ einen eindeutigen Rückschluss auf das untersuchte Objekt zu. Da Rückschlüsse in beide Richtungen möglich sind, spricht man beim Isomorphismus von einer eineindeutigen Zuordnung von Zahlen zu Objekten. Dies setzt voraus, das bei der Datenerhebung jedem Objekt eine verschiedene Zahl zugeordnet werden kann.

Peter, Paul und Patrick werden verhaftet, da sie Züge mit Graffiti besprüht haben. Peter, Paul und Patrick erhalten eine individuelle Sträflingsnummer. (Peter erhält die Sträflingsnummer 100, Paul die 200 und Patrick die 300.) Alle drei Befragten erhalten also verschiedene Zahlen im numerischen Relativ . so kann man beispielsweise von der Zahl 300 den Rückschluss ziehen, dass es sich um Patrick handelt. Es liegt eine isomorphe Abbildung vor.
(Im obigen "Sportbeispiel" kann ich von der Zahl 1 keinen Rückschluss ziehen, ob sie der Angabe von Peter oder von Paul entstammt).

Ausgelagerte Bildbeschreibung von Isomorphismus und Homomorphismus