Rangordnungen: Unterschied zwischen den Versionen
Micha (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{Nav||Messen komplexer Merkmale|Urteilen}} =Rangordnungen= Bei Rangordnungen ordnen Urteiler Objekte durch direkten Vergleich. Im Gegensatz zu [Ratingskalen]…“) |
Elisa (Diskussion | Beiträge) |
||
| Zeile 95: | Zeile 95: | ||
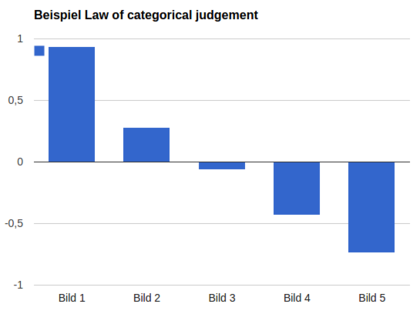
Es ergibt sich also zum Beispiel für die in Bild 5 dargestellte Person eine Ausprägung des Merkmals "sympathisches Auftreten" von -0,74. Allen beurteilten Objekten wird ein Wert zugewiesen, es ergibt sich eine Intervallskala. Dementsprechend ist es auch möglich, die Daten nach der Umrechnung auf der Skala mittels Addition zu verschieben, um z.B. nur positive Werte zu erhalten – die Intervalle zwischen den Datenpunkten (=Bildern) ändert sich dabei nicht. | Es ergibt sich also zum Beispiel für die in Bild 5 dargestellte Person eine Ausprägung des Merkmals "sympathisches Auftreten" von -0,74. Allen beurteilten Objekten wird ein Wert zugewiesen, es ergibt sich eine Intervallskala. Dementsprechend ist es auch möglich, die Daten nach der Umrechnung auf der Skala mittels Addition zu verschieben, um z.B. nur positive Werte zu erhalten – die Intervalle zwischen den Datenpunkten (=Bildern) ändert sich dabei nicht. | ||
[[File:Diagramm_rangordnungen.png|420px]] | [[File:Diagramm_rangordnungen.png|420px|link=Ausgelagerte_Bildbeschreibungen#Law_of_categorical_judgement|Ausgelagerte Bildbeschreibung zu Law of categorical jugdement]] | ||
Aktuelle Version vom 4. Dezember 2021, 14:59 Uhr
Rangordnungen
Bei Rangordnungen ordnen Urteiler Objekte durch direkten Vergleich. Im Gegensatz zu [Ratingskalen] hat dieses Vorgehen den Vorteil, dass der Urteilende sich nicht auf einen bestimmten festen Wert festgelegen muss, sondern die Objekte im Bezug aufeinander relativ beurteilt. Allerdings hat dies auch den Nachteil, dass eine solche Rangordnung mit steigender Anzahl der Objekte schnell unübersichtlich wird. Dementsprechend ist das direkte Ordnen nur für wenige Objekte angebracht – mit Hilfe der Technik der sukzessiven Intervalle kann dieser Nachteil teilweise ausgeglichen werden.
Direkte Rangordnungen
Der Urteiler ordnet die Objekte der Reihe nach, von größter Ausprägung zu geringster Ausprägung. Haben mehrere Objekte die gleiche Ausprägung, werden die Rangplätze gemittelt. (z.B. 1; 2,5; 2,5; 4; … oder 1; 2; 4; 4; 4; 6).
Sukzessive Intervalle
Der Urteiler ordnet die Objekte in Gruppen. Diese Gruppen können sich entweder beim Sortieren durch den Urteiler ergeben – oder bereits vorgegeben sein (damit wäre man wieder nahe bei einer [Ratingskala]). Dieses Vorgehen ist besonders sinnvoll, wenn viele Objekte geordnet werden sollen.
Skalieren von Rangordnungen: Law of categorical judgement
Das “Law of categorical judgement” ist eine Methode, mittels der die Daten aus einer Rangordnung von einer [Ordinalskala] in eine [Intervallskala] umgewandelt werden können. Diese Methode basiert auf der Annahme, dass Urteile über Objekte normalverteilt sind und dass die Bewertungen bei mehrfacher Beurteilung um einen "wahren" Wert herum streuen.
Bei dieser Methode wird zunächst eine Reihe von Objekten von mehreren Urteilern (oder seltener: mehrmals von einem Urteiler) nach der Methode der sukzessiven Intervalle beurteilt.
Beispielsweise bewerten 50 Urteiler in einer sozialpsychologischen Studie das Auftreten von Personen in Bildern, indem sie es einer von fünf Rangkategorien zuordnen: “sympathisch” =1, “eher sympathisch”=2, “weder sympathisch noch unsympathisch”=3, “eher unsympathisch”=4 und “unsympathisch”=5. Es nun 5 Bilder, und entsprechend der Anzahl von 50 Urteilern, 50 Urteile pro Bild, die sich auf die verschiedenen Stufen verteilen.
Es ergibt sich die folgende Häufigkeitentabelle:
| \ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Bild 1 | 2 | 8 | 10 | 13 | 17 |
| Bild 2 | 5 | 10 | 15 | 18 | 2 |
| Bild 3 | 10 | 12 | 20 | 5 | 3 |
| Bild 4 | 15 | 20 | 10 | 3 | 2 |
| Bild 5 | 22 | 18 | 7 | 2 | 1 |
Da jedes Bild von 50 Urteilern bewertet wurde ergeben sich nun die relativen Häufigkeiten (absolute Häufigkeit / 50):
| \ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Bild 1 | 0,04 | 0,16 | 0,2 | 0,26 | 0,34 |
| Bild 2 | 0,1 | 0,2 | 0,3 | 0,36 | 0,04 |
| Bild 3 | 0,2 | 0,24 | 0,4 | 0,1 | 0,06 |
| Bild 4 | 0,3 | 0,4 | 0,2 | 0,06 | 0,04 |
| Bild 5 | 0,44 | 0,36 | 0,14 | 0,04 | 0,02 |
sowie die kummulierten relativen Häufigkeiten (also jede Spalte auf die nächste aufaddiert, von links startend):
| \ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Bild 1 | 0,04 | 0,2 | 0,4 | 0,66 | 1 |
| Bild 2 | 0,1 | 0,3 | 0,6 | 0,96 | 1 |
| Bild 3 | 0,2 | 0,44 | 0,84 | 0,94 | 1 |
| Bild 4 | 0,3 | 0,7 | 0,9 | 0,96 | 1 |
| Bild 5 | 0,44 | 0,8 | 0,94 | 0,98 | 1 |
Nun werden diesen kumulativen Häufigkeiten z-Werte der Normalverteilung zugeordnet. Damit verwirklicht man die Annahme, dass die Urteile normalverteilt um einen Mittelwert streuen.
Nachdem die Häufigkeiten in z-Werte transformiert wurden, werden die Spaltensummen, Zeilensummen, Zeilenmittel und Kategoriengrenzen bestimmt.
Die Ausprägung für jedes Objekt entspricht nun den Differenzen zwischen durchschnittlicher Kategoriengrenze (0,33) und den jeweiligen Mittelwerten der Zeilen.
| \ | 1 | 2 | 3 | 4 | ∑ | ø | Ausprägung |
|---|---|---|---|---|---|---|---|
| Bild 1 | -1,75 | -0,84 | -0,25 | 0,41 | -2,43 | -0,61 | 0,94 |
| Bild 2 | -1,28 | -0,52 | 0,25 | 1,75 | 0,2 | 0,05 | 0,28 |
| Bild 3 | 0,84 | -0,15 | 0,99 | 1,55 | 1,55 | 0,39 | -0,06 |
| Bild 4 | -0,52 | 0,52 | 1,28 | 1,75 | 3,03 | 0,76 | -0,43 |
| Bild 5 | -0,15 | 0,84 | 1,55 | 2,05 | 4,29 | 1,07 | -0,74 |
| ∑ | -4,54 | 0,15 | 3,82 | 7,51 | |||
| Kategoriengrenzen | -0,91 | -0,03 | 0,76 | 1,5 | 0,33 |
Es ergibt sich also zum Beispiel für die in Bild 5 dargestellte Person eine Ausprägung des Merkmals "sympathisches Auftreten" von -0,74. Allen beurteilten Objekten wird ein Wert zugewiesen, es ergibt sich eine Intervallskala. Dementsprechend ist es auch möglich, die Daten nach der Umrechnung auf der Skala mittels Addition zu verschieben, um z.B. nur positive Werte zu erhalten – die Intervalle zwischen den Datenpunkten (=Bildern) ändert sich dabei nicht.