Analyse: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Nav|Navigation|Experimente|Versuchsplanung}} In der Analyse von Versuchsergebnissen stellt sich im Groben folgende Frage: <br/> Stammen die gemessenen Daten…“) |
Elisa (Diskussion | Beiträge) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Experimente|Versuchsplanung}} | {{Nav|Navigation|Experimente|Versuchsplanung}} | ||
In der Analyse von Versuchsergebnissen stellt sich | In der Analyse von Versuchsergebnissen stellt sich oft folgende Frage: <br/> | ||
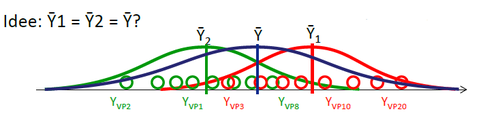
Stammen die gemessenen Daten der 2 Bedingungen aus 2 verschiedenen Populationen (nämlich eine Population in der Bedingung 1 und die andere Population in der Bedingung 2), oder sind es zufällig leicht verschiedene Daten ein und derselben Population (kein Unterschied zwischen Bedingung 1 und 2): <br/> <br/> | Stammen die gemessenen Daten der 2 Bedingungen aus 2 verschiedenen Populationen (nämlich eine Population in der Bedingung 1 und die andere Population in der Bedingung 2), oder sind es zufällig leicht verschiedene Daten ein und derselben Population (kein Unterschied zwischen Bedingung 1 und 2): <br/> <br/> | ||
[[Datei:Analyse1.png|500px|zentriert]] | [[Datei:Analyse1.png|500px|zentriert|link=Ausgelagerte_Bildbeschreibungen#Analyse_Versuchsplanung|Ausgelagerte Bildbeschreibung von Analyse Versuchsplanung]] | ||
<br/> <br/>Bei der Antwort auf diese Frage beruft man sich oftmals auf statistische Überlegungen, auf deren Basis man die Irrtumswahrscheinlichkeit p bestimmt. P gibt hierbei an, wie wahrscheinlich es ist, einen Unterschied zwischen zwei Gruppen in den vorliegenden Daten zu finden, wenn alle Messwerte in Wirklichkeit aus einer Population stammen (die Unterschiede in den Werten also nicht auf Unterschiede der Bedingungen zurückzuführen sind, sondern auf Zufallsschwankungen und/oder Messfehler). | <br/> <br/>Bei der Antwort auf diese Frage beruft man sich oftmals auf statistische Überlegungen, auf deren Basis man die Irrtumswahrscheinlichkeit p bestimmt. P gibt hierbei an, wie wahrscheinlich es ist, einen Unterschied zwischen zwei Gruppen in den vorliegenden Daten zu finden, wenn alle Messwerte in Wirklichkeit aus einer Population stammen (die Unterschiede in den Werten also nicht auf Unterschiede der Bedingungen zurückzuführen sind, sondern auf Zufallsschwankungen und/oder Messfehler). Anders formuliert: wie wahrscheinlich ist es, das vorliegende Messergebnis oder noch mehr der [https://de.wikipedia.org/wiki/Hypothese_%28Statistik%29 Nullhypothese] widersprechende Ergebnisse zu finden, obwohl sie (HO) zutrifft? | ||
P gibt somit auch an, wie groß die Wahrscheinlichkeit eines [[Alpha-Fehler|Alpha-Fehlers]] ist – also dass wir einen Unterschied zwischen den Bedingungen annehmen, obwohl keiner existiert. Das Entscheidungsproblem in dieser Frage beschreibt die [[Entscheiden: Signaldetektion|Signalentdeckungstheorie]] genauer. <br/> <br/> | |||
Für das Überprüfen der Unterschiedlichkeit gibt es je nach Faktorstufenanzahl verschiedene Herangehensweisen. <br/> <br/> | Für das Überprüfen der Unterschiedlichkeit gibt es je nach Faktorstufenanzahl verschiedene Herangehensweisen. <br/> <br/> | ||
==2 | ==2 Gruppen== | ||
Bei metrischen Daten (wenn die AV auf einer Intervall- oder Verhältnisskala erfasst wurde) wird oftmals ein t-Test verwendet. <br/> <br/> | Bei metrischen Daten (wenn die AV auf einer Intervall- oder Verhältnisskala erfasst wurde) wird oftmals ein t-Test verwendet. <br/> <br/> | ||
Der t-Test für unabhängige Stichproben wird bei Zufallsgruppendesigns (between subjects) verwendet. Er untersucht die Unterschiedlichkeit der Gruppen anhand der Streuung der Einzelwerte. Er vergleicht die Varianz '''zwischen''' den Gruppen mit der Varianz '''innerhalb''' der Gruppen. <br/> <br/> | Der t-Test für unabhängige Stichproben wird bei Zufallsgruppendesigns (between subjects) verwendet. Er untersucht die Unterschiedlichkeit der Gruppen anhand der Streuung der Einzelwerte. Er vergleicht die Varianz '''zwischen''' den Gruppen mit der Varianz '''innerhalb''' der Gruppen. <br/> <br/> | ||
Der t-Test für abhängige Stichproben wird bei Messwiederholungsdesigns (within subjects) und Block/Parallelisierungs-Designs (matched groups ) verwendet. Auch hier wird der Unterschied zwischen den Messungen im Verhältnis zur Gesamtstreuung untersucht, allerdings kann die Varianz zwischen einzelnen Messeinheiten (z.B. Versuchspersonen oder parallelisierte Paare) vorher abgezogen werden. Die unterliegende Idee ist dabei folgende: die Voraussetzungen (sprich: die Ausprägung eventueller Störgrößen) zweier Messwerte sind jeweils vergleichbar – entweder weil sie von demselben Individuum, oder weil sie von zwei parallelisierten Versuchspersonen stammen. Aufgrund dieser Vergleichbarkeit kann man die beiden Messwerte (z.B. Experimentalwert von Kontrollgruppenwert) voneinander abziehen. Zurück bleibt nur der Effekt. Dies ist wünschenswert, da hierdurch ein Teil der Varianz (nämlich die Unterschiede in den Voraussetzungen zu '''anderen''' Versuchspersonen) schon herausgerechnet wird. Es wird auf gewisse Art nur überprüft, ob sich die Differenz der Bedingungen von 0 unterscheidet. <br/> <br/>[[Datei:Analyse2.png|500px|zentriert]]<br/> <br/> | Der t-Test für abhängige Stichproben wird bei Messwiederholungsdesigns (within subjects) und Block/Parallelisierungs-Designs (matched groups ) verwendet. Auch hier wird der Unterschied zwischen den Messungen im Verhältnis zur Gesamtstreuung untersucht, allerdings kann die Varianz zwischen einzelnen Messeinheiten (z.B. Versuchspersonen oder parallelisierte Paare) vorher abgezogen werden. Die unterliegende Idee ist dabei folgende: die Voraussetzungen (sprich: die Ausprägung eventueller Störgrößen) zweier Messwerte sind jeweils vergleichbar – entweder weil sie von demselben Individuum, oder weil sie von zwei parallelisierten Versuchspersonen stammen. Aufgrund dieser Vergleichbarkeit kann man die beiden Messwerte (z.B. Experimentalwert von Kontrollgruppenwert) voneinander abziehen. Zurück bleibt nur der Effekt. Dies ist wünschenswert, da hierdurch ein Teil der Varianz (nämlich die Unterschiede in den Voraussetzungen zu '''anderen''' Versuchspersonen) schon herausgerechnet wird. Es wird auf gewisse Art nur überprüft, ob sich die Differenz der Bedingungen von 0 unterscheidet. <br/> <br/>[[Datei:Analyse2.png|500px|zentriert|link=Ausgelagerte_Bildbeschreibungen#Analyse_2_Gruppen|Ausgelagerte Bildbeschreibung von Analyse 2 Gruppen]]<br/> <br/> | ||
==Mehr als 2 | |||
Eine UV mit mehr als 2 Stufen liefert z.B. bei nicht-linearen Zusammenhängen zwischen [[UV]] und [[AV]] zuverlässigere Informationen. Jedoch ist die Analyse der Daten anspruchsvoller. <br/> <br/>[[Datei:Analyse3.png|500px|zentriert]]<br/> <br/> | ==Mehr als 2 Gruppen== | ||
Eine UV mit mehr als 2 Stufen liefert z.B. bei nicht-linearen Zusammenhängen zwischen [[unabhängige Variablen|UV]] und [[abhängige Variablen|AV]] zuverlässigere Informationen. Jedoch ist die Analyse der Daten anspruchsvoller. <br/> <br/>[[Datei:Analyse3.png|500px|zentriert|link=Ausgelagerte_Bildbeschreibungen#Analyse_Fließdiagramm|Ausgelagerte Bildbeschreibung von Analyse Fließdiagramm]]<br/> <br/> | |||
Durch die größere Anzahl der Stufen ergeben sich mehr als 2 Gruppen, die miteinander verglichen werden müssen. Ein einfacher t-Test reicht also nicht mehr aus. <br/> <br/> | Durch die größere Anzahl der Stufen ergeben sich mehr als 2 Gruppen, die miteinander verglichen werden müssen. Ein einfacher t-Test reicht also nicht mehr aus. <br/> <br/> | ||
Ein einfacher Ansatz wäre, mehrere t-Tests zu kombinieren und somit die Verteilungen alle untereinander zu vergleichen. Hierbei stellt sich jedoch das Problem der '''Alpha-Fehler-Akkumulierung''': Mit jedem Test wächst das Risiko, einen Unterschied zwischen Gruppen rein aus Zufall zu finden - obwohl sie also eigentlich derselben Population entstammen (siehe [[Entscheiden: Signaldetektion|Signaldetektion]]). <br/> | Ein einfacher Ansatz wäre, mehrere t-Tests zu kombinieren und somit die Verteilungen alle untereinander zu vergleichen. Hierbei stellt sich jedoch das Problem der '''Alpha-Fehler-Akkumulierung''': Mit jedem Test wächst das Risiko, einen Unterschied zwischen Gruppen rein aus Zufall zu finden - obwohl sie also eigentlich derselben Population entstammen (siehe [[Entscheiden: Signaldetektion|Signaldetektion]]). <br/> | ||
Um das Alpha-Niveau auf 5% zu halten, kann eine '''Bonferroni-Korrektur''' vorgenommen werden. Diese setzt das Niveau für die einzelnen Tests so fest, dass insgesamt die Wahrscheinlichkeit für einen Alpha-Fehler nicht über 5% steigt. Das führt jedoch dazu, dass in den einzelnen Tests das Alpha-Niveau deutlich geringer ist als üblich – und damit die Wahrscheinlichkeit für einen Beta-Fehler (einen wahrhaftigen Unterschied nicht zu entdecken) steigt. <br/> <br/> | Um das Alpha-Niveau auf 5% zu halten, kann eine '''Bonferroni-Korrektur''' vorgenommen werden. Diese setzt das Niveau für die einzelnen Tests so fest, dass insgesamt die Wahrscheinlichkeit für einen Alpha-Fehler nicht über 5% steigt. Das führt jedoch dazu, dass in den einzelnen Tests das Alpha-Niveau deutlich geringer ist als üblich – und damit die Wahrscheinlichkeit für einen Beta-Fehler (einen wahrhaftigen Unterschied nicht zu entdecken) steigt. <br/> <br/> | ||
Bei metrischen Daten wird deshalb üblicherweise eine einfaktorielle Varianzanalyse (Analysis of Variance – ANOVA) durchgeführt.<br/> | Bei metrischen Daten wird deshalb üblicherweise eine einfaktorielle Varianzanalyse (Analysis of Variance – ANOVA) durchgeführt.<br/> | ||
Hier stellt man die systematische Varianz (also die durch die Manipulation verursachte Varianz - die Varianz zwischen den Gruppen) der Fehlervarianz (zufällige oder durch individuelle Unterschiede verursachte Varianz innerhalb der Gruppen) gegenüber. Die ANOVA liefert einem also die Information, ob zwischen Gruppen verlässliche Unterschiede vorliegen – sie sagt aber nicht, zwischen welchen der Gruppen die Unterschiede sind. Deshalb wird sie auch als „Omnibus“-Test bezeichnet. Durch | Hier stellt man die systematische Varianz (also die durch die Manipulation verursachte Varianz - die Varianz zwischen den Gruppen) der Fehlervarianz (zufällige oder durch individuelle Unterschiede verursachte Varianz innerhalb der Gruppen) gegenüber. Die ANOVA liefert einem also die Information, ob zwischen Gruppen verlässliche Unterschiede vorliegen – sie sagt aber nicht, zwischen welchen der Gruppen die Unterschiede sind. Deshalb wird sie auch als „Omnibus“-Test bezeichnet. Durch multiple Vergleiche können im Fall eines positiven Ergebnisses der ANOVA anschließend (post-hoc) die Unterschied genauer Bestimmt werden.<br/> <br/> | ||
Wie beim einfachen t-Test unterscheidet sich die Vorgehensweise bei der ANOVA zwischen Within- und Between-Designs. <br/> <br/> | Wie beim einfachen t-Test unterscheidet sich die Vorgehensweise bei der ANOVA zwischen Within- und Between-Designs. <br/> <br/> | ||
Aktuelle Version vom 25. März 2022, 13:37 Uhr
In der Analyse von Versuchsergebnissen stellt sich oft folgende Frage:
Stammen die gemessenen Daten der 2 Bedingungen aus 2 verschiedenen Populationen (nämlich eine Population in der Bedingung 1 und die andere Population in der Bedingung 2), oder sind es zufällig leicht verschiedene Daten ein und derselben Population (kein Unterschied zwischen Bedingung 1 und 2):
Bei der Antwort auf diese Frage beruft man sich oftmals auf statistische Überlegungen, auf deren Basis man die Irrtumswahrscheinlichkeit p bestimmt. P gibt hierbei an, wie wahrscheinlich es ist, einen Unterschied zwischen zwei Gruppen in den vorliegenden Daten zu finden, wenn alle Messwerte in Wirklichkeit aus einer Population stammen (die Unterschiede in den Werten also nicht auf Unterschiede der Bedingungen zurückzuführen sind, sondern auf Zufallsschwankungen und/oder Messfehler). Anders formuliert: wie wahrscheinlich ist es, das vorliegende Messergebnis oder noch mehr der Nullhypothese widersprechende Ergebnisse zu finden, obwohl sie (HO) zutrifft?
P gibt somit auch an, wie groß die Wahrscheinlichkeit eines Alpha-Fehlers ist – also dass wir einen Unterschied zwischen den Bedingungen annehmen, obwohl keiner existiert. Das Entscheidungsproblem in dieser Frage beschreibt die Signalentdeckungstheorie genauer.
Für das Überprüfen der Unterschiedlichkeit gibt es je nach Faktorstufenanzahl verschiedene Herangehensweisen.
2 Gruppen
Bei metrischen Daten (wenn die AV auf einer Intervall- oder Verhältnisskala erfasst wurde) wird oftmals ein t-Test verwendet.
Der t-Test für unabhängige Stichproben wird bei Zufallsgruppendesigns (between subjects) verwendet. Er untersucht die Unterschiedlichkeit der Gruppen anhand der Streuung der Einzelwerte. Er vergleicht die Varianz zwischen den Gruppen mit der Varianz innerhalb der Gruppen.
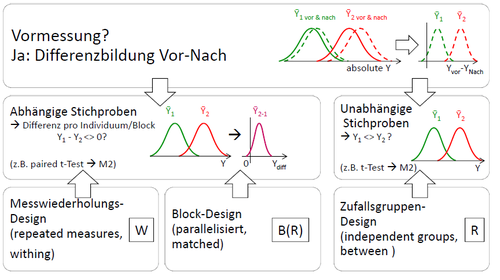
Der t-Test für abhängige Stichproben wird bei Messwiederholungsdesigns (within subjects) und Block/Parallelisierungs-Designs (matched groups ) verwendet. Auch hier wird der Unterschied zwischen den Messungen im Verhältnis zur Gesamtstreuung untersucht, allerdings kann die Varianz zwischen einzelnen Messeinheiten (z.B. Versuchspersonen oder parallelisierte Paare) vorher abgezogen werden. Die unterliegende Idee ist dabei folgende: die Voraussetzungen (sprich: die Ausprägung eventueller Störgrößen) zweier Messwerte sind jeweils vergleichbar – entweder weil sie von demselben Individuum, oder weil sie von zwei parallelisierten Versuchspersonen stammen. Aufgrund dieser Vergleichbarkeit kann man die beiden Messwerte (z.B. Experimentalwert von Kontrollgruppenwert) voneinander abziehen. Zurück bleibt nur der Effekt. Dies ist wünschenswert, da hierdurch ein Teil der Varianz (nämlich die Unterschiede in den Voraussetzungen zu anderen Versuchspersonen) schon herausgerechnet wird. Es wird auf gewisse Art nur überprüft, ob sich die Differenz der Bedingungen von 0 unterscheidet.
Mehr als 2 Gruppen
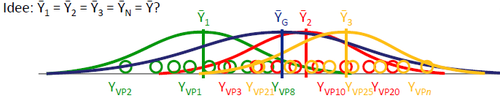
Eine UV mit mehr als 2 Stufen liefert z.B. bei nicht-linearen Zusammenhängen zwischen UV und AV zuverlässigere Informationen. Jedoch ist die Analyse der Daten anspruchsvoller.
Durch die größere Anzahl der Stufen ergeben sich mehr als 2 Gruppen, die miteinander verglichen werden müssen. Ein einfacher t-Test reicht also nicht mehr aus.
Ein einfacher Ansatz wäre, mehrere t-Tests zu kombinieren und somit die Verteilungen alle untereinander zu vergleichen. Hierbei stellt sich jedoch das Problem der Alpha-Fehler-Akkumulierung: Mit jedem Test wächst das Risiko, einen Unterschied zwischen Gruppen rein aus Zufall zu finden - obwohl sie also eigentlich derselben Population entstammen (siehe Signaldetektion).
Um das Alpha-Niveau auf 5% zu halten, kann eine Bonferroni-Korrektur vorgenommen werden. Diese setzt das Niveau für die einzelnen Tests so fest, dass insgesamt die Wahrscheinlichkeit für einen Alpha-Fehler nicht über 5% steigt. Das führt jedoch dazu, dass in den einzelnen Tests das Alpha-Niveau deutlich geringer ist als üblich – und damit die Wahrscheinlichkeit für einen Beta-Fehler (einen wahrhaftigen Unterschied nicht zu entdecken) steigt.
Bei metrischen Daten wird deshalb üblicherweise eine einfaktorielle Varianzanalyse (Analysis of Variance – ANOVA) durchgeführt.
Hier stellt man die systematische Varianz (also die durch die Manipulation verursachte Varianz - die Varianz zwischen den Gruppen) der Fehlervarianz (zufällige oder durch individuelle Unterschiede verursachte Varianz innerhalb der Gruppen) gegenüber. Die ANOVA liefert einem also die Information, ob zwischen Gruppen verlässliche Unterschiede vorliegen – sie sagt aber nicht, zwischen welchen der Gruppen die Unterschiede sind. Deshalb wird sie auch als „Omnibus“-Test bezeichnet. Durch multiple Vergleiche können im Fall eines positiven Ergebnisses der ANOVA anschließend (post-hoc) die Unterschied genauer Bestimmt werden.
Wie beim einfachen t-Test unterscheidet sich die Vorgehensweise bei der ANOVA zwischen Within- und Between-Designs.