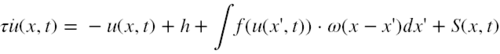Dynamic Neural Fields: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Neuronale Netze|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Neuronale Netze|Kognitive Modellierung|Hauptseite}} | ||
== Dynamic Field Theory (DFT) == | |||
Kognitionen werden als dynamischer Prozess verstanden. Daher lassen sie sich mittels dynamischer Systeme beschreiben. Diese bestehen aus Systemvariablen, die durch Differentialgleichungen modelliert werden, sodass der Systemzustand als Kombination der Ausprägungen der relevanten Systemvariablen zu jedem Zeitpunkt berechnet werden kann. | |||
Dynamische neuronale Felder (Dynamic Neural Fields, DNF) sind dynamische Systeme auf Basis [[Neuronale Netze|neuronaler Netzwerkmodelle]]. Der Fokus liegt dabei auf der zeitlichen und räumlichen Ausbreitung von Aktivierungen, durch die dynamische kognitive Prozesse beschrieben werden sollen. Neuronenpopulationen werden durch Knoten repräsentiert, welche in einer Schicht ein- oder zweidimensional angeordnet und lateral miteinander verknüpft sind, sodass sie sich gegenseitig beeinflussen können. Zudem können mehrere Felder miteinander verknüpft sein und sich dadurch ebenfalls beeinflussen. Als Modell eignen sich dynamische neuronale Felder zum Beispiel zur Vorhersage von Blick- oder Mausbewegungen oder zur Modellierung räumlicher Aufmerksamkeit. | |||
Zum Verständnis dynamischer neuronaler Felder bedarf es dreier Bausteine, welche im Folgenden näher erklärt werden. | |||
=== Populationsvektoren === | |||
Die DFT geht davon aus, dass eine Population von Knoten gemeinsam eine Eigenschaftsdimension kodiert. Dies beruht auf dem Befund, dass kognitive Prozesse dadurch entstehen, dass Neuronenpopulationen lokal miteinander interagieren. Dies kann man sich am Beispiel der Blickbewegung verdeutlichen: Jedes Neuron hat eine „bevorzugte Richtung“, für die es am stärksten feuert. Für ähnliche Richtungen feuert es ebenfalls, jedoch immer schwächer, je geringer die Ähnlichkeit ist. Wenn man verschiedene dieser Neuronen zusammenfasst, gelangt man zu einer kontinuierlichen Repräsentation des gesamten Kontinuums an Blickbewegungsrichtungen. Die Eigenschaftsausprägung ergibt sich also daraus, wie stark verschiedene Knoten mit unterschiedlichen „bevorzugten“ Ausprägungen feuern. Bei dieser Zusammenfassung spricht man von einem Populationsvektor. In einem dynamischen neuronalen Feld wird jede Eigenschaft durch eine Dimension von Knoten kodiert. | |||
=== Interaktionen im DNF === | |||
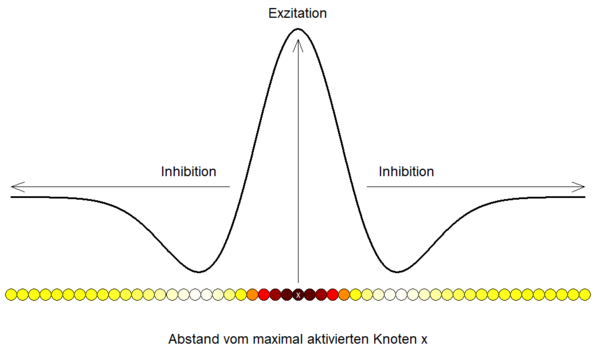
Die miteinander verknüpften Knoten im dynamischen Feld beeinflussen sich gegenseitig und stabilisieren dadurch Aktivierungsmuster im Feld. Die Art der Interaktion lässt sich unterteilen in lokale Exzitation und Inhibition sowie globale Inhibition. | |||
*Lokale Exzitation: <br> nah beieinander liegende Knoten verstärken sich gegenseitig, sodass eine Aktivierungsspitze aufrechterhalten werden kann und vor dem Abflachen geschützt wird. | |||
*Lokale Inhibition: <br> Knoten, die sich etwas weiter weg in der Umgebung der Aktivierungsspitze befinden, werden gehemmt, sodass die Ausbreitung der Aktivierung eingeschränkt wird. | |||
*Globale Inhibition:<br> weit entfernte Knoten werden ebenfalls gehemmt, um die Entstehung weiterer Aktivierungsspitzen zu unterdrücken. | |||
Diese Form der Interaktion lässt sich als Mexican-Hat-Funktion implementieren: | |||
[[Datei:Mexican_hat.PNG|600px|link=Ausgelagerte_Bildbeschreibungen#Mexican-Hat-Funktion|Ausgelagerte Bildbeschreibung von Mexican-Hat-Funktion]] | |||
=== Entwicklung über die Zeit === | |||
Durch die gegenseitige Beeinflussung der Knoten ändern sich die Aktivierungsmuster über die Zeit. Die räumliche Verschiebung von Aktivierungsmaxima gibt Auskunft über sich ändernde Ausprägungen der Eigenschaftsdimensionen. Die Höhe der Aktivierungsmaxima variiert in Abhängigkeit von Input und lateralen Interaktionen zwischen den Feldknoten ebenfalls. Die Aktivierung der Knoten lässt sich mit folgender Formel beschreiben: | |||
[[Datei:Dnf.png|500px|link=Ausgelagerte_Formeln#Aktivierung der Knoten|Ausgelagerte Formel Aktivierung der Knoten]] | |||
* x – ein Knoten | |||
* x' – ein Nachbarknoten | |||
* u(x,t) – Aktivierung u eines Knotens x zum Zeitpunkt t | |||
* τ – Zeitkonstante | |||
* h – Ruhepotential | |||
* f – (meist) sigmoidale Aktivierungsfunktion | |||
* ω – Interaktionskernel (Mexican-Hat-Funktion) | |||
* S(x,t) – externer stimulusbedingter Input für jeden Knoten x zu jedem Zeitpunkt t | |||
Die Veränderung der Aktivierung eines Knotens hängt demnach von seiner vorherigen Aktivierung und seinem Ruhepotential ab. Des Weiteren wird sie durch einen möglichen externen Input und die Interaktion mit Nachbarknoten beeinflusst. | |||
Darüber hinaus existiert ein Schwellwert, der bestimmt, ob eine Aktivierungsspitze über die Zeitdauer des Inputs hinaus aufrechterhalten werden kann. Wenn der Input nicht stark genug ist, um die Aktivierungsstärke über den Schwellwert zu bringen, bleibt die Aktivierung in der Nähe des Ruhepotentials und verschwindet nach dem Ende des Inputs. Wird der Schwellwert hingegen überschritten, entsteht eine stabile Aktivierungsspitze. | |||
Aktuelle Version vom 5. Januar 2022, 14:46 Uhr
Dynamic Field Theory (DFT)
Kognitionen werden als dynamischer Prozess verstanden. Daher lassen sie sich mittels dynamischer Systeme beschreiben. Diese bestehen aus Systemvariablen, die durch Differentialgleichungen modelliert werden, sodass der Systemzustand als Kombination der Ausprägungen der relevanten Systemvariablen zu jedem Zeitpunkt berechnet werden kann. Dynamische neuronale Felder (Dynamic Neural Fields, DNF) sind dynamische Systeme auf Basis neuronaler Netzwerkmodelle. Der Fokus liegt dabei auf der zeitlichen und räumlichen Ausbreitung von Aktivierungen, durch die dynamische kognitive Prozesse beschrieben werden sollen. Neuronenpopulationen werden durch Knoten repräsentiert, welche in einer Schicht ein- oder zweidimensional angeordnet und lateral miteinander verknüpft sind, sodass sie sich gegenseitig beeinflussen können. Zudem können mehrere Felder miteinander verknüpft sein und sich dadurch ebenfalls beeinflussen. Als Modell eignen sich dynamische neuronale Felder zum Beispiel zur Vorhersage von Blick- oder Mausbewegungen oder zur Modellierung räumlicher Aufmerksamkeit.
Zum Verständnis dynamischer neuronaler Felder bedarf es dreier Bausteine, welche im Folgenden näher erklärt werden.
Populationsvektoren
Die DFT geht davon aus, dass eine Population von Knoten gemeinsam eine Eigenschaftsdimension kodiert. Dies beruht auf dem Befund, dass kognitive Prozesse dadurch entstehen, dass Neuronenpopulationen lokal miteinander interagieren. Dies kann man sich am Beispiel der Blickbewegung verdeutlichen: Jedes Neuron hat eine „bevorzugte Richtung“, für die es am stärksten feuert. Für ähnliche Richtungen feuert es ebenfalls, jedoch immer schwächer, je geringer die Ähnlichkeit ist. Wenn man verschiedene dieser Neuronen zusammenfasst, gelangt man zu einer kontinuierlichen Repräsentation des gesamten Kontinuums an Blickbewegungsrichtungen. Die Eigenschaftsausprägung ergibt sich also daraus, wie stark verschiedene Knoten mit unterschiedlichen „bevorzugten“ Ausprägungen feuern. Bei dieser Zusammenfassung spricht man von einem Populationsvektor. In einem dynamischen neuronalen Feld wird jede Eigenschaft durch eine Dimension von Knoten kodiert.
Interaktionen im DNF
Die miteinander verknüpften Knoten im dynamischen Feld beeinflussen sich gegenseitig und stabilisieren dadurch Aktivierungsmuster im Feld. Die Art der Interaktion lässt sich unterteilen in lokale Exzitation und Inhibition sowie globale Inhibition.
- Lokale Exzitation:
nah beieinander liegende Knoten verstärken sich gegenseitig, sodass eine Aktivierungsspitze aufrechterhalten werden kann und vor dem Abflachen geschützt wird. - Lokale Inhibition:
Knoten, die sich etwas weiter weg in der Umgebung der Aktivierungsspitze befinden, werden gehemmt, sodass die Ausbreitung der Aktivierung eingeschränkt wird. - Globale Inhibition:
weit entfernte Knoten werden ebenfalls gehemmt, um die Entstehung weiterer Aktivierungsspitzen zu unterdrücken.
Diese Form der Interaktion lässt sich als Mexican-Hat-Funktion implementieren:
Entwicklung über die Zeit
Durch die gegenseitige Beeinflussung der Knoten ändern sich die Aktivierungsmuster über die Zeit. Die räumliche Verschiebung von Aktivierungsmaxima gibt Auskunft über sich ändernde Ausprägungen der Eigenschaftsdimensionen. Die Höhe der Aktivierungsmaxima variiert in Abhängigkeit von Input und lateralen Interaktionen zwischen den Feldknoten ebenfalls. Die Aktivierung der Knoten lässt sich mit folgender Formel beschreiben:
- x – ein Knoten
- x' – ein Nachbarknoten
- u(x,t) – Aktivierung u eines Knotens x zum Zeitpunkt t
- τ – Zeitkonstante
- h – Ruhepotential
- f – (meist) sigmoidale Aktivierungsfunktion
- ω – Interaktionskernel (Mexican-Hat-Funktion)
- S(x,t) – externer stimulusbedingter Input für jeden Knoten x zu jedem Zeitpunkt t
Die Veränderung der Aktivierung eines Knotens hängt demnach von seiner vorherigen Aktivierung und seinem Ruhepotential ab. Des Weiteren wird sie durch einen möglichen externen Input und die Interaktion mit Nachbarknoten beeinflusst.
Darüber hinaus existiert ein Schwellwert, der bestimmt, ob eine Aktivierungsspitze über die Zeitdauer des Inputs hinaus aufrechterhalten werden kann. Wenn der Input nicht stark genug ist, um die Aktivierungsstärke über den Schwellwert zu bringen, bleibt die Aktivierung in der Nähe des Ruhepotentials und verschwindet nach dem Ende des Inputs. Wird der Schwellwert hingegen überschritten, entsteht eine stabile Aktivierungsspitze.