Entstehung des Standardfehlers: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Statistik|Hauptseite}} | {{Nav|Navigation|Statistik|Hauptseite}} | ||
Der | Der Standardfehler ist eine sehr wichtige statistische Kenngröße, die die Grundlage vieler statistischer Tests darstellt, zum Beispiel in regressionsanalytischen Verfahren. In diesem Text und in der App wird exemplarisch auf den Standardfehler des Mittelwertes eingegangen. | ||
Der Standardfehler des Mittelwertes ist ein statistisches Maß für die Genauigkeit der Schätzung des Populationsmittelwertes. Er entspricht der Standardabweichung der Verteilungen der Punktschätzungen des Populationsmittelwertes von Stichproben des Umfangs n einer Population. | |||
Der Standardfehler ist von der Standardabweichung in der Population und der Stichprobengröße abhängig und lässt sich in der Form σ_(X̅) = σ/√n darstellen. Ist die Streuung der Stichprobenmittelwerte um den Populationsmittelwert gering, kann der Populationsmittelwert genauer aus dem Mittelwert einer einzelnen Stichprobe geschätzt werden. Bei größerer Standardabweichung σ in der Population steigt demnach der Standardfehler an, wohingegen er bei größeren Stichprobenumfängen n geringer wird. Weil in der Praxis weder der Standardfehler des arithmetischen Mittelwertes noch die Standardabweichung aus der Population bekannt ist, wird der Standardfehler des Stichprobenmittelwertes s_(X̅) als Schätzwert für σ_(X̅) verwendet. s_(X̅) wird dabei mithilfe der Standardabweichung s und dem Stichprobenumfang n aus den bekannten Daten der Stichprobe geschätzt. | |||
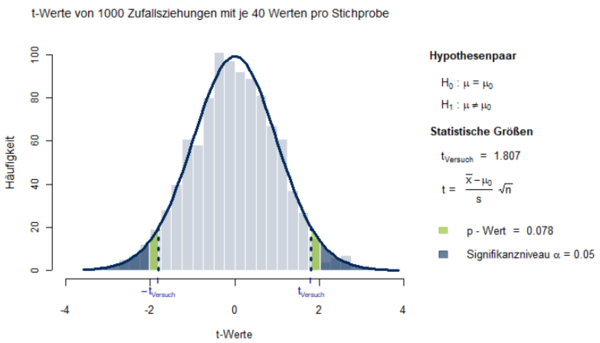
In einer Grundgesamtheit aus Berufstätigen beträgt der mit dem Emotion Regulation Questionnaire (ERQ) erfasste Mittelwert im kognitiven Umdeuten von stressigen Situationen im Alltag (Reappraisal) µ = 25. Die Standardabweichung in dieser Grundgesamtheit beträgt σ = 6. Zieht man aus dieser Grundgesamtheit 500 Zufallsstichproben der Größe n = 150, dann streuen die Mittelwerte der 500 Stichproben normalverteilt um den tatsächlichen Populationsmittelwert (vgl. Abb.1). | |||
In | |||
[[File:p_Wert_1.png|600px|Abbildung 1: Verteilung der t-Werte und Darstellung des p-Wertes bei zweiseitiger Fragestellung]] | [[File:p_Wert_1.png|600px|Abbildung 1: Verteilung der t-Werte und Darstellung des p-Wertes bei zweiseitiger Fragestellung]] | ||
Da in diesem fiktiven Beispiel die Standardabweichung der Grundgesamtheit bekannt ist, kann der Standardfehler direkt aus der Standardabweichung σ = 6 und der Stichprobengröße n = 150 berechnet werden. Der Standardfehler des Mittelwerts beträgt hier σ_(X̅) = 0.49. Die aus den Parametern der Stichproben ermittelte Standardabweichung der gezogenen Mittelwerte beträgt s_((X̅)) = 0.48 und weicht somit nur minimal von σ_(X̅) ab. Bei einer geringeren Anzahl an Zufallsziehungen wäre diese Schätzung ungenauer. Die Standardabweichung der gezogenen 500 Mittelwerte s_((X̅)) darf nicht mit dem Standardfehler eines einzelnen Stichprobenmittelwertes s_(X̅) verwechselt werden, welcher aus den Parametern s und n der einzelnen Stichprobe berechnet und in der Praxis für die Schätzung des Standardfehlers des arithmetischen Mittelwerts genutzt wird. | |||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/pwertlink.html | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/pwertlink.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird der | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird der Standardfehler näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ | ||
|120px]] <span style="color: white"> kkk </span> Inwieweit der | |120px]] <span style="color: white"> kkk </span> Inwieweit der Standardfehler von verschiedenen Parametern abhängig ist, lässt sich in der interaktiven Simulation zum [http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ Standardfehler] grafisch nachvollziehen. | ||
| Zeile 29: | Zeile 22: | ||
'''''Weiterführende Literatur''''' | '''''Weiterführende Literatur''''' | ||
Rudolf, M., & Kuhlisch, W. (2008). ''Biostatistik: Eine Einführung für Biowissenschaftler'' (Kapitel | Rudolf, M., & Kuhlisch, W. (2008). ''Biostatistik: Eine Einführung für Biowissenschaftler'' (Kapitel 4.2). München: Pearson Studium. | ||
Version vom 4. März 2020, 19:17 Uhr
Der Standardfehler ist eine sehr wichtige statistische Kenngröße, die die Grundlage vieler statistischer Tests darstellt, zum Beispiel in regressionsanalytischen Verfahren. In diesem Text und in der App wird exemplarisch auf den Standardfehler des Mittelwertes eingegangen. Der Standardfehler des Mittelwertes ist ein statistisches Maß für die Genauigkeit der Schätzung des Populationsmittelwertes. Er entspricht der Standardabweichung der Verteilungen der Punktschätzungen des Populationsmittelwertes von Stichproben des Umfangs n einer Population.
Der Standardfehler ist von der Standardabweichung in der Population und der Stichprobengröße abhängig und lässt sich in der Form σ_(X̅) = σ/√n darstellen. Ist die Streuung der Stichprobenmittelwerte um den Populationsmittelwert gering, kann der Populationsmittelwert genauer aus dem Mittelwert einer einzelnen Stichprobe geschätzt werden. Bei größerer Standardabweichung σ in der Population steigt demnach der Standardfehler an, wohingegen er bei größeren Stichprobenumfängen n geringer wird. Weil in der Praxis weder der Standardfehler des arithmetischen Mittelwertes noch die Standardabweichung aus der Population bekannt ist, wird der Standardfehler des Stichprobenmittelwertes s_(X̅) als Schätzwert für σ_(X̅) verwendet. s_(X̅) wird dabei mithilfe der Standardabweichung s und dem Stichprobenumfang n aus den bekannten Daten der Stichprobe geschätzt.
In einer Grundgesamtheit aus Berufstätigen beträgt der mit dem Emotion Regulation Questionnaire (ERQ) erfasste Mittelwert im kognitiven Umdeuten von stressigen Situationen im Alltag (Reappraisal) µ = 25. Die Standardabweichung in dieser Grundgesamtheit beträgt σ = 6. Zieht man aus dieser Grundgesamtheit 500 Zufallsstichproben der Größe n = 150, dann streuen die Mittelwerte der 500 Stichproben normalverteilt um den tatsächlichen Populationsmittelwert (vgl. Abb.1).
Da in diesem fiktiven Beispiel die Standardabweichung der Grundgesamtheit bekannt ist, kann der Standardfehler direkt aus der Standardabweichung σ = 6 und der Stichprobengröße n = 150 berechnet werden. Der Standardfehler des Mittelwerts beträgt hier σ_(X̅) = 0.49. Die aus den Parametern der Stichproben ermittelte Standardabweichung der gezogenen Mittelwerte beträgt s_((X̅)) = 0.48 und weicht somit nur minimal von σ_(X̅) ab. Bei einer geringeren Anzahl an Zufallsziehungen wäre diese Schätzung ungenauer. Die Standardabweichung der gezogenen 500 Mittelwerte s_((X̅)) darf nicht mit dem Standardfehler eines einzelnen Stichprobenmittelwertes s_(X̅) verwechselt werden, welcher aus den Parametern s und n der einzelnen Stichprobe berechnet und in der Praxis für die Schätzung des Standardfehlers des arithmetischen Mittelwerts genutzt wird.
kkk Im Video wird der Standardfehler näher erläutert.
kkk Inwieweit der Standardfehler von verschiedenen Parametern abhängig ist, lässt sich in der interaktiven Simulation zum Standardfehler grafisch nachvollziehen.
Weiterführende Literatur
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 4.2). München: Pearson Studium.