Rescorla Wagner: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Mathematische Modelle|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Mathematische Modelle|Kognitive Modellierung|Hauptseite}} | ||
Das Rescorla-Wagner (RW) Modell von Robert Rescorla und Allan Wagner ist ein mathematisches Modell der [https://de.wikipedia.org/wiki/Klassische_Konditionierung Klassischen Konditionierung]. Bereits 1905 konnte Iwan Pawlow beobachten, dass ein Hund, der auf die Präsentation von Futter jedes Mal mit Speichelfluss reagierte, nach ein paar Durchgängen auch auf die alleinige Präsentation eines Glockentons speichelte, wenn der Ton in den vorherigen Durchgängen dem Futter vorausging. In der Methode der Klassischen Konditionierung wird für gewöhnlich ein neutraler Stimulus (z.B. ein Ton), der sog. konditionierte Stimulus (CS), in mehreren Durchgängen kurz vor einem reaktionsauslösenden (= unkonditionierten) Stimulus (US, z.B. Futter) präsentiert, bis nach einiger Zeit auch der neutrale Reiz allein die entsprechende Reaktion (Speichelfluss) auslöst. Als zugrundliegenden Prozess vermutet man eine sich kontinuierlich verstärkende Verknüpfung bzw. Assoziation zwischen CS und US. Das RW-Modell beschreibt die durch einen Konditionierungsdurchgang erfolgenden Veränderungen in der Assoziationsstärke zwischen dem CS und dem darauffolgenden US durch folgende Formel: | |||
[[File:Rescorla-Wagner F1.png|center|600px]] | |||
* '''V''' = Assoziationsstärke der Reize (CS+US) | |||
* '''α''' = Lernrate | |||
* '''λ''' = Stärke des präsentierten US (z.B. λ=1, wenn US; λ=0, wenn kein US) | |||
* '''t''' = Lerndurchgänge / Trial Nummer | |||
Zentrales Prinzip des Modells ist, dass Lernen durch Überraschung bzw. Vorhersagefehler entsteht. Überraschung oder Vorhersagefehler ist im Modell repräsentiert als (λ - Vt-1) oder δ, also die Differenz zwischen Realität (Präsenz / Stärke des US) und Vorhersage/Erwartung (über die Durchgänge akkumulierte Assoziationsstärke). | |||
Der Vorhersagefehler wird dann auf das bisherige V addiert, sodass sich die Assoziationsstärke des folgenden Durchgangs entsprechend verändert. Während des Lernvorgangs wird die Differenz zwischen Erwartungen und Realität immer geringer, sodass sich der Vorhersagefehler und damit auch der Lernzuwachs pro Durchgang vermindern. | |||
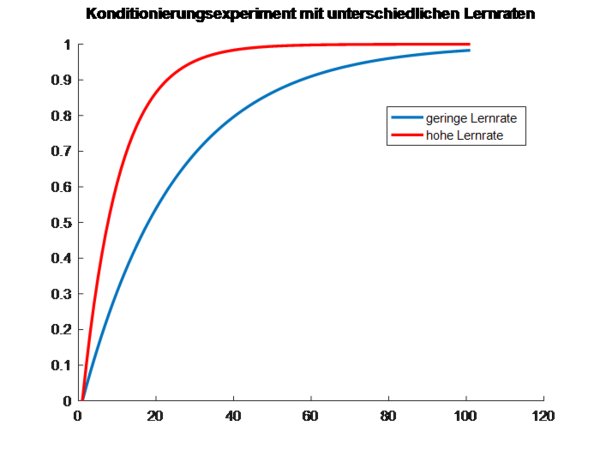
In der Beispielgrafik unten führen wir ein Konditionierungsexperiment mit zwei Versuchspersonen durch, die eine unterschiedliche Lernrate aufweisen. Nach einem Ton (CS) wird jedes Mal ein Luftstoß ins Auge gepustet (US), auf den die Personen mit einem Blinzeln reagieren. Die Versuchspersonen wissen am Anfang des Experimentes noch nicht, dass der Ton und der Luftstoß zusammenhängen, haben also eine Assoziationsstärke V=0; sie können den Luftstoß nicht vorhersagen. Dessen überraschendes Eintreten führt somit zu einem Lerneffekt, einer Erhöhung von V. Je stärker der CS und US assoziiert werden, desto besser können die Teilnehmenden den Luftstoß anhand des Tons vorhersagen. Das Lernen durch den US nimmt also stetig ab und stagniert irgendwann. Vor allem bei der Person mit hoher Lernrate (rot), zeigt sich ein schnelles Plateau bereits vor der Hälfte des Experimentes. | |||
[[File:Rescorla-Wagner Lernrate.png||600px]] | |||
Verschiedene Effekte aus der Lernpsychologie konnten mit Hilfe des RW-Modells erklärt werden, z.B. der [https://portal.hogrefe.com/dorsch/blockierung/ Blocking-Effekt] oder die [http://lexikon.stangl.eu/15343/inhibitorische-konditionierung/ inhibitorische Konditionierung]. | |||
Auch werden Abwandlungen des RW-Modells für Algorithmen [[Neuronale Netze|Neuronaler Netze] oder dem [[Reinforcement Learning|Reinforcement Learning]] genutzt. In diesem Zusammenhang wird dann von überwachtem Lernen (supervised learning) mit einer [[Deltaregel|Delta-Regel]] gesprochen. | |||
Version vom 24. September 2018, 15:51 Uhr
Das Rescorla-Wagner (RW) Modell von Robert Rescorla und Allan Wagner ist ein mathematisches Modell der Klassischen Konditionierung. Bereits 1905 konnte Iwan Pawlow beobachten, dass ein Hund, der auf die Präsentation von Futter jedes Mal mit Speichelfluss reagierte, nach ein paar Durchgängen auch auf die alleinige Präsentation eines Glockentons speichelte, wenn der Ton in den vorherigen Durchgängen dem Futter vorausging. In der Methode der Klassischen Konditionierung wird für gewöhnlich ein neutraler Stimulus (z.B. ein Ton), der sog. konditionierte Stimulus (CS), in mehreren Durchgängen kurz vor einem reaktionsauslösenden (= unkonditionierten) Stimulus (US, z.B. Futter) präsentiert, bis nach einiger Zeit auch der neutrale Reiz allein die entsprechende Reaktion (Speichelfluss) auslöst. Als zugrundliegenden Prozess vermutet man eine sich kontinuierlich verstärkende Verknüpfung bzw. Assoziation zwischen CS und US. Das RW-Modell beschreibt die durch einen Konditionierungsdurchgang erfolgenden Veränderungen in der Assoziationsstärke zwischen dem CS und dem darauffolgenden US durch folgende Formel:
- V = Assoziationsstärke der Reize (CS+US)
- α = Lernrate
- λ = Stärke des präsentierten US (z.B. λ=1, wenn US; λ=0, wenn kein US)
- t = Lerndurchgänge / Trial Nummer
Zentrales Prinzip des Modells ist, dass Lernen durch Überraschung bzw. Vorhersagefehler entsteht. Überraschung oder Vorhersagefehler ist im Modell repräsentiert als (λ - Vt-1) oder δ, also die Differenz zwischen Realität (Präsenz / Stärke des US) und Vorhersage/Erwartung (über die Durchgänge akkumulierte Assoziationsstärke).
Der Vorhersagefehler wird dann auf das bisherige V addiert, sodass sich die Assoziationsstärke des folgenden Durchgangs entsprechend verändert. Während des Lernvorgangs wird die Differenz zwischen Erwartungen und Realität immer geringer, sodass sich der Vorhersagefehler und damit auch der Lernzuwachs pro Durchgang vermindern.
In der Beispielgrafik unten führen wir ein Konditionierungsexperiment mit zwei Versuchspersonen durch, die eine unterschiedliche Lernrate aufweisen. Nach einem Ton (CS) wird jedes Mal ein Luftstoß ins Auge gepustet (US), auf den die Personen mit einem Blinzeln reagieren. Die Versuchspersonen wissen am Anfang des Experimentes noch nicht, dass der Ton und der Luftstoß zusammenhängen, haben also eine Assoziationsstärke V=0; sie können den Luftstoß nicht vorhersagen. Dessen überraschendes Eintreten führt somit zu einem Lerneffekt, einer Erhöhung von V. Je stärker der CS und US assoziiert werden, desto besser können die Teilnehmenden den Luftstoß anhand des Tons vorhersagen. Das Lernen durch den US nimmt also stetig ab und stagniert irgendwann. Vor allem bei der Person mit hoher Lernrate (rot), zeigt sich ein schnelles Plateau bereits vor der Hälfte des Experimentes.
Verschiedene Effekte aus der Lernpsychologie konnten mit Hilfe des RW-Modells erklärt werden, z.B. der Blocking-Effekt oder die inhibitorische Konditionierung.
Auch werden Abwandlungen des RW-Modells für Algorithmen [[Neuronale Netze|Neuronaler Netze] oder dem Reinforcement Learning genutzt. In diesem Zusammenhang wird dann von überwachtem Lernen (supervised learning) mit einer Delta-Regel gesprochen.