Einführung Statistische Modelle
Um ein statistische Modell zu entwerfen, werden (quantitative) Daten benötigt. Statistische Modelle beschreiben die Daten bestimmter Fälle, beziehen sich also nur auf diese. Sie sind dadurch in der Regel nicht generalisierbar. Die Daten werden abstrahiert durch z.B. das Bilden des geeigneten Mittelwertes und der Standardabweichung und häufig auch reduziert durch einfaches Wegwerfen von als unwesentlich erachteten Informationen. Zum Beispiel geht bei Beschreibung des Zusammenhangs zwischen zwei gemessenen Variablen (siehe unten) durch eine Gerade natürlich die tatsächliche Streuung (der Fehler) verloren. Die durch die Abstraktion aufgetretenen "Fehler" im Bezug auf die Originaldaten werden versucht zu minimieren (fitten des Modells an die Daten). Existierende Daten können anschließend mit dem Modell verglichen werden, je nachdem wie sie passen machen sie die Beschreibungsgüte des statistischen Modells sichtbar (Güte des Fits).
Beispiel für ein einfaches statistisches Modell ist die lineare Regression
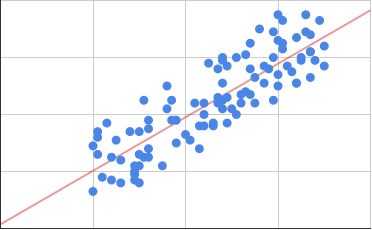
Die Daten im Bild sind wild verteilt und folgen offensichtlich keiner eindeutigen mathematischen Funktion o.ä.. Ebenfalls offensichtlich ist aber, dass sie nicht komplett zufällig liegen und dass es sehr wohl einen linearen Zusammenhang gibt. Man kann diese Wolke nun durch eine Regressionsgerade (rot) vereinfacht darstellen. Die Gleichung dieser Geraden ist dann ein Modell für diesen Zusammenhang zwischen Ängstlichkeit und Intelligenz
Im Vergleich zu mathematischen und komputationalen Modellen haben haben statistische Modelle kaum theoriebildenden Wert, da sie nicht über konkrete abstrahieren (siehe Beispiel mathematische Modelle). Sie haben auch kein Eigenverhalten wie z.B. komputationale Modelle und können nicht überraschen, also neue unerwartete Vorhersagen generieren.