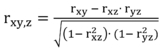Partialkorrelation
Die partielle Korrelation berechnet den von einer Störvariable bereinigten Korrelationskoeffizienten zweier Variablen. Dies kann z.B. dabei helfen, Scheinkorrelationen zu identifizieren und validere Aussagen über Zusammenhänge von Variablen zu treffen. Der Begriff der Scheinkorrelation sollte nicht missverstanden werden, da es die beobachtete Korrelation ja tatsächlich gibt. Gemeint ist er hier im Sinne von Scheinkausalität, dass es also keine reale Ursache-Wirkungs-Beziehung zwischen den Variablen gibt.
Scheinkorrelationen sind somit signifikant von Null verschiedene Korrelationen, die keinen real existierenden Zusammenhang widerspiegeln. Diese können entstehen, wenn die Korrelation zweier Variablen zu großen Teilen durch eine Störvariable erklärbar ist. Um Scheinkorrelationen und Störvariablen zu identifizieren, müssen inhaltliche Vorüberlegungen aufgestellt werden, da es nicht möglich ist, diese unmittelbar in den Daten zu erkennen. Wird der Einfluss der Störvariablen auf den untersuchten Zusammenhang eliminiert, erhält man die partielle Korrelation.
Das zugrundeliegende Prinzip der partiellen Korrelation ist die Korrelationsanalyse von Regressionsresiduen. Dafür werden zwei lineare Regressionen berechnet, in denen die Störvariable die zwei untersuchten Variablen vorhersagt. Die Regressionsresiduen entsprechen den Anteilen der Variablen, die nicht durch die Störvariable erklärt werden können. Für ein von der Störvariable unabhängiges Zusammenhangsmaß kann dementsprechend die Korrelation der Residuen beider Regressionen berechnet werden.
Zur formalen Berechnung des partiellen Korrelationskoeffizienten (rxy,z) benötigt man neben der untersuchten Korrelation zweier Variablen x und y (rxy) zusätzlich die Produkt-Moment-Korrelationen der beiden Variablen mit der Störvariable z (rxz und ryz). Mithilfe der folgenden Formel lässt sich anschließend der von z bereinigte lineare Zusammenhang der beiden Variablen berechnen:
Beispielstudie
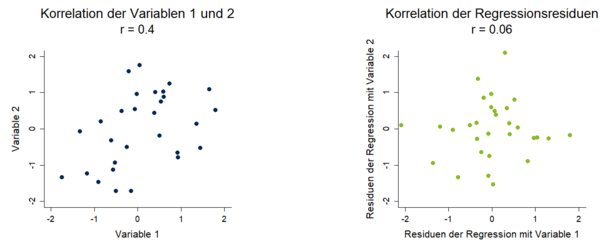
In einer fiktiven Studie wurde die Reaktionszeit (X) experimentell erfasst und mit dem Einkommen (Y) der Probanden korreliert. Da diese beiden Variablen in keinem inhaltlichen Zusammenhang stehen, wurde vorher angenommen, dass die Korrelation der beiden Variablen Null beträgt. In der vorliegenden Stichprobe wurde jedoch eine signifikant von Null verschiedene Korrelation rxy = 0.4 berechnet. Da theoretisch nicht begründbar ist, dass ein höheres Einkommen mit längeren Reaktionszeiten einhergeht, wird angenommen, dass es sich um eine Scheinkorrelation handelt, die dadurch erklärbar ist, dass sowohl die Reaktionszeit als auch das Einkommen positiv mit der Störvariable Alter (Z) zusammenhängen. Dafür werden die Korrelationen rxz = ryz = 0.6 beider Variablen mit dem Alter der Probanden erfasst. Um die vom Alter bereinigte partielle Korrelation zu bestimmen, werden die Regressionsresiduen miteinander korreliert bzw. die vorliegenden Werte in die Formel eingesetzt. Der partielle Korrelationskoeffizient zwischen Reaktionszeit und Alter beträgt rxy,z = 0.0625 und ist nicht signifikant von Null verschieden. Der positive Zusammenhang zwischen Reaktionszeit und Einkommen ist nach Eliminierung des Einflusses der Störvariable verschwunden, was darauf hindeutet, dass es sich um eine Scheinkorrelation handelt. In Abbildung 1 wird die Korrelation vor und nach Elimination der Störvariable mit Streudiagrammen veranschaulicht.
kkk Im Video wird die partielle Korrelation näher erläutert.
kkk Wie der partielle Korrelationskoeffizient von der Korrelationen mit der Störvariable abhängig ist, lässt sich in der interaktiven Simulation nachvollziehen.
Weiterführende Literatur
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.5). München: Pearson Studium.