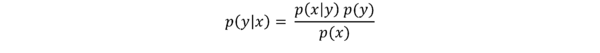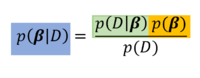Probabilistische Modelle
Kognitive Prozesse, wie zum Beispiel Wahrnehmungsurteile, beruhen auf unsicheren Schlussfolgerungen und müssen daher die Unsicherheit der Informationen berücksichtigen. Wenn man in der Dunkelheit die Umrisse einer bekannten Person erkennt, dann ist es wichtig, die Unsicherheit dieser Einschätzung im Kopf zu haben um sein Verhalten entsprechend anzupassen (und keinem ggf. gefährlichen Unbekannten unvorsichtig in die Arme zu rennen).
Im Gegensatz zu deterministischen Modellen berücksichtigen probabilistische Modelle explizit diese Unsicherheit in den Inputs und Outputs eines Verarbeitungsprozesses. Durch Quantifizierung der Unsicherheit (Zuverlässigkeit / Risiko) in den Messungen, den Modellparametern und der Passung des Modells an die Daten geben probabilistische Vorhersagen eine Reihe oder Verteilung an möglichen Outcomes vor statt einer Einzeleinschätzung. Dies wird einer komplexen und verrauschten Realität in der Regel besser gerecht. Doch wie repräsentiert man Unsicherheit?
Wahrscheinlichkeitstheoretische Grundlagen
Probabilistische Modelle sind mathematische Modelle, die Zufallsvariablen und Wahrscheinlichkeitsverteilungen miteinschließen. Zufallsvariablen stellen das potentielle Ergebnis eines unsicheren Ereignisses dar (z.B. die Augenzahl eines Würfelwurfs); sie bilden Ereignisse als Zahlen ab. Wahrscheinlichkeitsverteilungen weisen den verschiedenen potentiellen Ergebnissen Wahrscheinlichkeitswerte zu (z.B. 1/6 für jede der sechs Augenzahlen).
Wenn wir X als unsere Zufallsvariable über eine Menge von messbaren Ereignissen definieren, dann gibt uns P(X = x) die Wahrscheinlichkeit, dass X den spezifischen Wert x annimmt (kurz geschrieben: p(x)). Alle diese Wahrscheinlichkeiten sind positiv und sie summieren sich über die Ausprägungen der Zufallsvariable zu 1 auf.
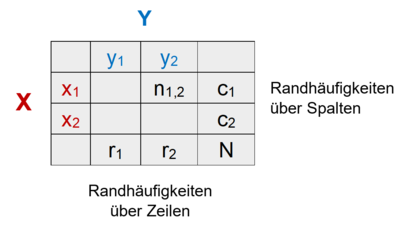
Wichtige Begriffe aus der probabilistischen Theorie zum Auftreten von Merkmalskombinationen lassen sich durch eine Kontingenztafel veranschaulichen, die in ihren Zellen die Häufigkeiten nij für die Ereigniskombinationen der Zufallsvariablen X und Y enthält. Diese Ereignishäufigkeiten nij ergeben über alle Kombinationen summiert die Gesamthäufigkeit N und addieren sich an den Seiten zu den Randhäufigkeiten auf, jeweils über die Zeilen (rj ) und Spalten (ci ) der Kontingenztafel:
Die Verbundwahrscheinlichkeit der Ereignisse xi und yj, d.h. die Wahrscheinlichkeit ihres gleichzeitigen Eintretens ist:
Also die Häufigkeit mit der diese Ereignisse gemeinsam auftreten nij durch die Häufigkeit aller Ereigniskombinationen N.
Die Randwahrscheinlichkeit bezeichnet die Wahrscheinlichkeit für die Ausprägung einer Zufallsvariable über die Ausprägungen der anderen Zufallsvariablen hinweg, also die relative Wahrscheinlichkeit für die Ereignisse einer bestimmten Reihe oder Spalte der Kontingenztafel bzw. die jeweilige Randhäufigkeit durch die Gesamthäufigkeit N. Für eine bestimmte Reihe lautet die Formel:
Die bedingte Wahrscheinlichkeit P(Y | X) ist die Wahrscheinlichkeit des Eintretens eines Ereignisses aus Y unter der Bedingung, dass das Eintreten eines Ereignisses aus X bereits bekannt ist. Sie berechnet sich aus der Häufigkeit des Eintretens beider Ereignisse und der Randhäufigkeit des bedingenden Ereignisses:
Über die Produktregel kann man die Verbundwahrscheinlichkeit zweier Ereignisse über die bedingte Wahrscheinlichkeit und die Randwahrscheinlichkeit berechnen:
Wenn wir die Produktregel nun umstellen erhalten wir:
Diese Formel geht auf den Satz des englischen Mathematikers Thomas Bayes zurück, laut dem sich für zwei Ereignisse X und Y die Wahrscheinlichkeit von Y, unter der Bedingung, dass X eingetreten ist, durch die Wahrscheinlichkeit von X, unter der Bedingung, dass Y eingetreten ist, errechnen lässt. Der Satz von Bayes erlaubt es, Schlussfolgerungen umzukehren, d.h. ausgehend von einem bekannten Wert P(X|Y) den eigentlich interessierenden Wert P(Y|X) zu bestimmen.
Bayesianische Inferenz
Die Bayes’sche Regel ist die Basis für probabilistische Schlussfolgerung (Inferenz) und Lernen. Nehmen wir an, wir haben ein lineares (Regressions-)Modell mit den Parametern β:
Unser Ziel ist es, die β-Parameter herauszufinden, gegeben den Daten D (y- und x-Werte). Konkret wollen wir also wissen, wie wahrscheinlich ein bestimmter Wert eines β-Parameters (z.B. des Intercept β0) ist, wenn wir die Daten D vorliegen haben. Um diese Wahrscheinlichkeit zu bestimmen bzw. eine bedingte Wahrscheinlichkeitsverteilung für den β-Parameter zu erhalten, greifen wir dabei auf die obige Formel von Bayes zurück (β0 und β1 sind hier zusammengefasst, werden aber separat bestimmt):
In der Terminologie der bayesianischen Inferenz beinhaltet diese Formel einen Posterior (blau), der sich aus der Likelihood (grün) und dem Prior (gelb) berechnet.
Der Posterior bzw. die posteriore Wahrscheinlichkeit, ist die Wahrscheinlichkeit, die Parameter β mit den vorliegenden Daten zu finden. Sie errechnet sich laut der Formel aus der bedingten Wahrscheinlichkeit für die Daten, gegeben die Parameter (Likelihood) und der a-priori Wahrscheinlichkeit für die Parameter (relativiert an der Randwahrscheinlichkeit für die Daten).
Der a-priori Wahrscheinlichkeit für den Parameter bzw. der Prior repräsentiert die Vorerfahrungen (Welche Informationen habe ich über den Parameter aus der Empirie oder vorherigen Berechnungsdurchgängen?). Die angenommen möglichen Ausprägungen des Parameters und ihre Wahrscheinlichkeit werden durch eine Wahrscheinlichkeitsverteilung (Normal-, Bernoulli-, Gleichverteilung oder andere) modelliert. Stellen wir uns vor, wir haben aus vorherigen Studien oder Meta-Analysen eine gewisse Vorstellung darüber, wo der Slope unseres Regressionsmodells liegen könnte. Dieser konkrete Wert würde bei einer a-priori Normalverteilung den Mittelwert darstellen. Die Unsicherheit über unsere Annahme berücksichtigen wir dadurch, dass wir gleichzeitig auch die Streuung/Varianz unserer Normalverteilung für den Parameter festlegen. Bei maximaler Unsicherheit über den Prior, d.h. wenn wir keine Ahnung haben, wo der Parameterwert liegen könnte bzw. uns nicht festlegen wollen, werden die Wahrscheinlichkeiten für die Parameterausprägungen in Form einer Gleichverteilung bestimmt (d.h., alle Ausprägungen sind gleich wahrscheinlich).
Die Likelihood gibt uns die Wahrscheinlichkeit der Daten gegeben unsere Parameter. Wie wahrscheinlich ist die Verteilung unserer y- und x-Werte, wenn die Parameter bestimmte Werte annehmen? Wie kommen die Daten überhaupt zustande? (=> hier steckt das eigentliche Modell) Diese Wahrscheinlichkeit wird über ein Maximum-Likelihood Schätzungsverfahren berechnet. Über die Kombination der Likelihood für die Daten und der a-priori Wahrscheinlichkeit für die Parameter kann anschließend die posteriore Wahrscheinlichkeit für die Parameter, gegeben die Daten, bestimmt werden.
Der Posterior enthält eine von den (neuen) Daten informierte Schätzung für den Parameter (z.B. den Mittelwert oder Modalwert der Verteilung) sowie deren Unsicherheit (Streuung der Verteilung). Je mehr Daten in die Berechnung miteinbezogen werden, desto sicherer wird dabei die Schätzung (d.h., die Streuung des Posteriors nimmt ab).
Der Vorteil zu konventionellen (frequentistischen) statistischen Ansätzen liegt darin, dass wir nicht nur eine Schätzung, sondern immer gleich eine ganze Verteilung der gesuchten Parameter erhalten. Weiterhin ist es hier möglich, eigene Vorannahmen bzw. ältere Berechnungen über die Festlegung des Priors in die Analyse miteinzubeziehen.
Anwendung in der Forschung
Viele Modelle aus der Entscheidungsforschung oder den kognitiven Neurowissenschaften versuchen Informationsverarbeitungsprozesse als eine Form von bayesianischer Inferenz zu betrachten. Diesen Ansätzen nach haben Menschen (und andere Informationsverarbeitungssysteme) keinen direkten Zugang zur Realität, sondern müssen die wahren, jedoch versteckten Ursachen ihrer Wahrnehmungen und Empfindungen (hidden causes) über ihren Input (z.B. elektrische Signale von den sensorischen Organen) über ein Modell schlussfolgern/inferieren. Da das Inputmuster i.d.R. verrauscht ist und es auch mit einer gewissen Wahrscheinlichkeit mit alternativen Modellen erklärt werden könnte, erfolgt diese Inferenz jedes Mal mit einer gewissen Unsicherheit. Agenten modellieren also ihre Umgebung und sich selbst, indem sie die versteckten Ursachen mit deren Wahrscheinlichkeit a-priori auf Grundlage ihrer Vorerfahrungen annehmen (Was habe ich bisher gelernt und was erwarte ich in meiner Umwelt?) und gegeben dieser angenommen Ursachen die Wahrscheinlichkeit für den Dateninput vorausberechnen (Likelihood, häufig auch „Generatives Modell“ genannt). Wenn nun die Daten schrittweise ins System gelangen, können Agenten ihr Modell je nach Passung auf die Daten immer weiter aktualisieren (über Berechnung der posterioren Wahrscheinlichkeit für die hidden causes / Parameter). Bei diesem bayesianischen Lernen wird der durch den Dateninput aktualisierte Posterior zum Prior für den nächsten Durchgang u.s.w. Somit wird das Modell über die Zeit immer präziser, sofern die Umwelt konstant bleibt.
Beispiele für Probabilistische Modelle aus der Kognitions- und Neurowissenschaft sind die Helmholtz-Maschine, das Hierachical Gaussian Filtering, Predictive Coding oder das Freie Energie Prinzip.