Power-Vergleiche: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Statistik|Hauptseite}} | {{Nav|Navigation|Statistik|Hauptseite}} | ||
Power-Untersuchungen ermöglichen auf der Basis von Simulationen Einschätzungen über die Wahrscheinlichkeit, dass bestimmte statistische Tests unter gegebenen Parametern die | Power-Untersuchungen ermöglichen auf der Basis von Simulationen Einschätzungen über die Wahrscheinlichkeit, dass bestimmte statistische Tests unter gegebenen Parametern die Nullhypothese korrekterweise ablehnen (vgl. [[Teststärke]]). | ||
Um die Power eines Tests zu schätzen, können z.B. Monte-Carlo Simulationen durchgeführt werden (vgl. [[Robustheitsuntersuchungen]]). Am Beispiel des Mittelwertsvergleichs von zwei Stichproben werden dafür aus zwei Grundgesamtheiten mit unterschiedlichen Mittelwerten und gleichen Standardabweichungen jeweils eine große Menge an Stichproben der Größe n gezogen. Für jedes Stichprobenpaar wird dann die Teststatistik berechnet. Der Anteil aller Vergleiche, welche die Nullhypothese bei vorher festgelegtem α signifikant ablehnen, | Um die Power eines Tests zu schätzen, können z.B. Monte-Carlo Simulationen durchgeführt werden (vgl. [[Robustheitsuntersuchungen]]). Am Beispiel des Mittelwertsvergleichs von zwei Stichproben werden dafür aus zwei Grundgesamtheiten mit unterschiedlichen Mittelwerten und gleichen Standardabweichungen jeweils eine große Menge an Stichproben der Größe n gezogen. Für jedes Stichprobenpaar wird dann die Teststatistik berechnet. Der Anteil aller Vergleiche, welche die Nullhypothese bei vorher festgelegtem α signifikant ablehnen, entspricht in diesem Fall der Teststärke, da allen berechneten Teststatistiken ein realer Mittelwertsunterschied der Grundgesamtheiten zugrunde liegt. | ||
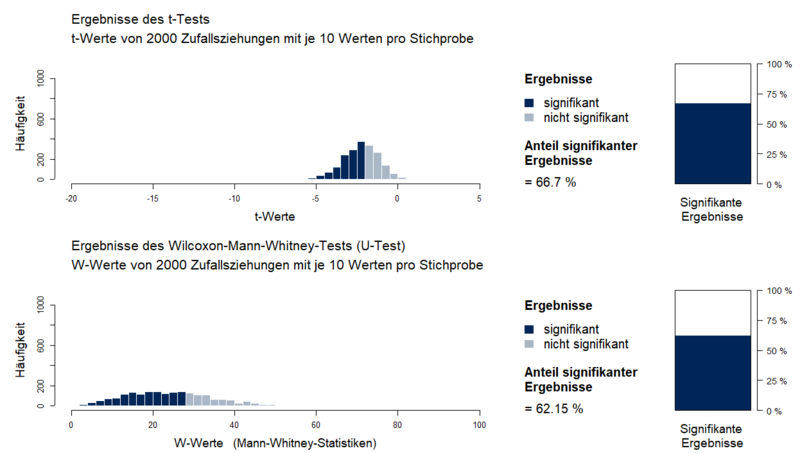
Ein Power-Vergleich vergleicht die Wahrscheinlichkeiten verschiedener statistischer Tests, unter gegebenen Parametern signifikante Ergebnisse zu erzielen. In Abbildung 1 wird z.B. der Vergleich zwischen t-Test und U-Test dargestellt. Dafür wurden aus zwei Grundgesamtheiten mit einem Mittelwertsunterschied von 1 und Standardabweichungen von σ = 1 jeweils 2000 Stichproben der Größe n = 10 gezogen. Die Voraussetzungen des t-Tests und des U-Tests seien erfüllt. | Ein Power-Vergleich vergleicht die Wahrscheinlichkeiten verschiedener statistischer Tests, unter gegebenen Parametern signifikante Ergebnisse zu erzielen. In Abbildung 1 wird z.B. der Vergleich zwischen t-Test und U-Test dargestellt. Dafür wurden aus zwei Grundgesamtheiten mit einem Mittelwertsunterschied von 1 und Standardabweichungen von σ = 1 jeweils 2000 Stichproben der Größe n = 10 gezogen. Die Voraussetzungen des t-Tests und des U-Tests seien erfüllt. | ||
| Zeile 13: | Zeile 11: | ||
Über jedes dieser 2000 Stichprobenpaare werden ein t-Test und ein U-Test gerechnet. Die Anteile der signifikanten Mittelwertsunterschiede (Power) werden im rechten Teil der Abbil-dung dargestellt. Bei gleichen Voraussetzungen werden beim t-Test etwa 4-5 % mehr | Über jedes dieser 2000 Stichprobenpaare werden ein t-Test und ein U-Test gerechnet. Die Anteile der signifikanten Mittelwertsunterschiede (Power) werden im rechten Teil der Abbil-dung dargestellt. Bei gleichen Voraussetzungen werden beim t-Test etwa 4-5 % mehr Mittelwertsunterschiede signifikant (66.7 %) als beim U-Test (62.15 %). Bei erfüllten Voraussetzungen sollte der t-Test dem U-Test dementsprechend vorgezogen werden. | ||
| Zeile 27: | Zeile 25: | ||
'''''Weiterführende Literatur''''' | '''''Weiterführende Literatur''''' | ||
Cohen, J. (1988). ''Statistical power analysis for the behavioral sciences''. Hillsdale, NY: Erlbaum. | |||
Version vom 5. März 2020, 23:59 Uhr
Power-Untersuchungen ermöglichen auf der Basis von Simulationen Einschätzungen über die Wahrscheinlichkeit, dass bestimmte statistische Tests unter gegebenen Parametern die Nullhypothese korrekterweise ablehnen (vgl. Teststärke).
Um die Power eines Tests zu schätzen, können z.B. Monte-Carlo Simulationen durchgeführt werden (vgl. Robustheitsuntersuchungen). Am Beispiel des Mittelwertsvergleichs von zwei Stichproben werden dafür aus zwei Grundgesamtheiten mit unterschiedlichen Mittelwerten und gleichen Standardabweichungen jeweils eine große Menge an Stichproben der Größe n gezogen. Für jedes Stichprobenpaar wird dann die Teststatistik berechnet. Der Anteil aller Vergleiche, welche die Nullhypothese bei vorher festgelegtem α signifikant ablehnen, entspricht in diesem Fall der Teststärke, da allen berechneten Teststatistiken ein realer Mittelwertsunterschied der Grundgesamtheiten zugrunde liegt.
Ein Power-Vergleich vergleicht die Wahrscheinlichkeiten verschiedener statistischer Tests, unter gegebenen Parametern signifikante Ergebnisse zu erzielen. In Abbildung 1 wird z.B. der Vergleich zwischen t-Test und U-Test dargestellt. Dafür wurden aus zwei Grundgesamtheiten mit einem Mittelwertsunterschied von 1 und Standardabweichungen von σ = 1 jeweils 2000 Stichproben der Größe n = 10 gezogen. Die Voraussetzungen des t-Tests und des U-Tests seien erfüllt.
Über jedes dieser 2000 Stichprobenpaare werden ein t-Test und ein U-Test gerechnet. Die Anteile der signifikanten Mittelwertsunterschiede (Power) werden im rechten Teil der Abbil-dung dargestellt. Bei gleichen Voraussetzungen werden beim t-Test etwa 4-5 % mehr Mittelwertsunterschiede signifikant (66.7 %) als beim U-Test (62.15 %). Bei erfüllten Voraussetzungen sollte der t-Test dem U-Test dementsprechend vorgezogen werden.
kkk Im Video werden Power-Vergleiche näher erläutert.
kkk In der interaktiven Simulation lassen sich Power-Vergleiche anhand von Monte-Carlo Simulationen für t-Tests und U-Tests bei verschiedenen Parameterwerten durchführen.
Weiterführende Literatur
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, NY: Erlbaum.