Backpropagation

Intuition des Backpropagationsverfahrens

Die Backpropagation-Regel ist ein überwachter Lernalgorithmus, der in künstlichen neuronalen Netzen verwendet wird. Im Gegensatz zur Deltaregel, auf der sie basiert, funktioniert Backpropagation auch bei Netzen mit beliebig vielen Hiddenschichten (hidden layers). Die Deltaregel gerät bei solchen Netzen an ihre Grenzen, da der gewünschte Output der Hiddenschichten nicht bekannt ist, sodass kein Fehlerterm für die Gewichtsmodifikation ermittelt werden kann. Backpropagation löst dieses Problem, indem Fehlerterme von der Outputschicht (output layer) schrittweise als Aktivierungen durch die einzelnen Schichten zurückgesendet werden. Die Gewichte können dann jeweils so angepasst werden, dass sich der Fehler verkleinert.

Ablauf des Algorithmus

1. Forward-Pass
   Zuerst wird ein Inputmuster präsentiert, dass für eine Ausbreitung von Aktivierungen im Netz bis zur Outputschicht sorgt. Der Output wird also wie gewöhnlich berechnet.
   
   
2. Berechnung des Fehlers
   Als nächstes wird die Differenz zwischen dem vorgegebenen korrekten Output und dem vom Netz erzeugten tatsächlichen Output ermittelt. Der Gesamtfehler ergibt sich, indem die Differenz zwischen Vorgabe und tatsächlicher Aktivierung für jeden Knoten i einzeln berechnet wird und diese Werte dann aufsummiert werden.
   
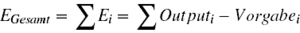
   Wenn der Fehler einen vorher festgelegten Grenzwert überschreitet, folgt der nächste Schritt. Ansonsten kann der Lernvorgang abgebrochen werden.
   
   
3. Backward-Pass
   Aus dem berechneten Fehler ergibt sich ein Fehlersignal, welches von der Outputschicht an die vorherige Hiddenschicht gesendet wird. Die Gewichte werden dann mittels eines Gradientenverfahrens so verändert, dass der Fehler sich verkleinert. Zunächst wird für jedes Gewicht zwischen der Outputschicht und der direkt davor liegenden Hiddenschicht berechnet, wie stark eine Veränderung dieses Gewichtes den Gesamtfehler beeinflussen würde.
   
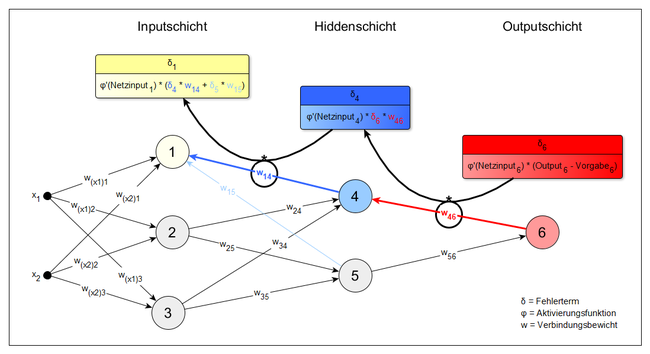
   In die Berechnung fließen die Aktivierung des Ursprungsknotens des Gewichts und ein Fehlerterm δ (siehe Abbildung) ein. Dies ergibt die Ableitung (den Gradienten) des Gesamtfehlers nach diesem Gewicht. Für das Gewicht w46 aus der Abbildung wäre dies zum Beispiel:
   
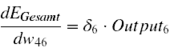
   Ist die Ableitung positiv, würde eine Gewichtserhöhung den Fehler vergrößern. Eine negative Ableitung hingegen bedeutet, dass der Fehler bei steigendem Gewicht sinkt. Daher wird ein jedes Gewicht verändert, indem die Ableitung des Gesamtfehlers nach diesem Gewicht (multipliziert mit einer Lernrate η) vom ursprünglichen Wert des Gewichtes subtrahiert wird. Das Gewicht w₄₆ wird demnach wie folgt verändert:
   
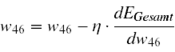
   Dies hat eine Verringerung des Gesamtfehlers zur Folge. Bevor die Gewichtsveränderung jedoch realisiert wird, muss das Verfahren noch für die Gewichte zwischen den vorhandenen Hiddenschichten und zwischen der Inputschicht und der ersten Hiddenschicht angewendet werden. Auch hier wird jeweils die Ableitung des Gesamtfehlers nach einem Gewicht berechnet, die dem Einfluss von Veränderungen dieses Gewichtes auf den Gesamtfehler entspricht. Wenn mehrere Knoten zur Aktivierung eines Knotens beitragen, muss dies im Fehlerterm δ berücksichtigt werden (Beispiel: Knoten 1 der oberen Abbildung). Danach werden die Gewichtsveränderungen entsprechend ermittelt. Angekommen bei der Inputschicht wird die berechnete Gewichtsveränderung für alle Gewichte des Netzes realisiert.
   
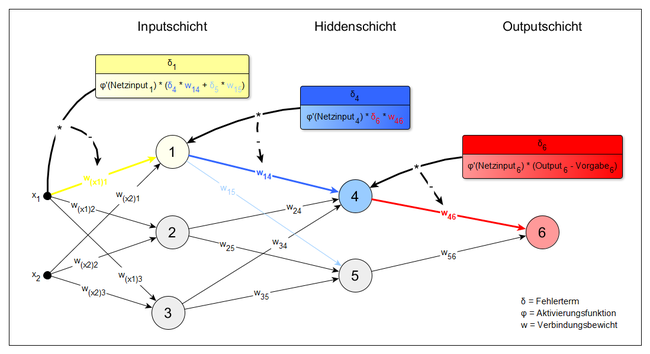
   Anschließend kehrt der Algorithmus zurück zu Schritt 1. Der Output des Netzes sollte nun mit jeder Iteration ein Stück näher am korrekten Output sein.

Vor- und Nachteile von Backpropagation

Backpropagation ist ein relativ wenig rechenaufwändiger Lernalgorithmus, der es ermöglicht, in mehrschichtigen Netzen zu lernen. Da Backpropagation letztlich einen Gradient Descent Algorithmus darstellt, übernimmt sie auch die Probleme dieses Verfahrens, so zum Beispiel, dass das globale Minimum zugunsten eines lokalen Minimums übersehen werden kann. Ein weiterer Nachteil ist, dass Netze, die Backpropagation nutzen, weniger gut zur biologisch plausiblen Nachbildung neuronaler Prozesse geeignet sind. Synapsen haben in der Natur eine Übertragungsrichtung. Bei der Backpropagation werden jedoch Signale in beide Richtungen durch ein und dieselbe Synapse geschickt. Wenn keine biologische Analogie angestrebt wird, spricht allerdings nichts gegen Backpropagation als rein mathematische Methode.