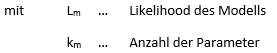Vergleichsmaße: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Modellvergleich|Kognitive Modellierung|Hauptseite}} | ||
Im Rahmen eines quantitativen Modellvergleichs wird die Balance zwischen möglichst geringer Parameteranzahl und guter Vorhersagefähigkeit verschiedener Modelle untersucht, um die Wahl eines optimalen Modells zu ermöglichen. Obwohl kein einheitliches Kriterium für diese Entscheidung existiert, kann die Berechnung von ''Vergleichsmaßen'' (auch als Informationskriterien bezeichnet) als Orientierung dienen. | Im Rahmen eines quantitativen Modellvergleichs wird die Balance zwischen möglichst geringer Parameteranzahl und guter Vorhersagefähigkeit verschiedener Modelle untersucht, um die Wahl eines optimalen Modells zu ermöglichen. Obwohl kein einheitliches Kriterium für diese Entscheidung existiert, kann die Berechnung von ''Vergleichsmaßen'' (auch als Informationskriterien bezeichnet) als Orientierung dienen. | ||
Diese Kriterien berücksichtigen nicht nur den Fit der Modelle an die empirischen Daten, sondern beachten zusätzlich die Anzahl der verwendeten Parameter. Dies ist wichtig, damit komplexere Modelle nicht grundsätzlich als besser eingestuft werden, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können. Das mit Hilfe der Vergleichsmaße ermittelte optimale Modell soll dabei das bestmögliche Verhältnis zwischen hoher Vorhersagefähigkeit und geringer Komplexität besitzen. | Diese Kriterien berücksichtigen nicht nur den Fit der Modelle an die empirischen Daten, sondern beachten zusätzlich die Anzahl der verwendeten Parameter. Dies ist wichtig, damit komplexere Modelle nicht grundsätzlich als besser eingestuft werden, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können. Das mit Hilfe der Vergleichsmaße ermittelte optimale Modell soll dabei das bestmögliche Verhältnis zwischen hoher Vorhersagefähigkeit und geringer Komplexität besitzen. | ||
| Zeile 6: | Zeile 6: | ||
== AIC == | == AIC == | ||
Das Akaike-Information-Criterion (AIC) wird zum Vergleich mehrerer Modelle basierend auf ihren Log-Likelihoodwerten verwendet. Je kleiner der AUC-Wert ist, umso besser ist der Fit des Modells. Der Log-Likelihoodwert ist umso größer, je besser das Modell die realen Daten vorhersagen kann. Um komplexere Modelle jedoch nicht grundsätzlich besser zu bewerten, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können und somit ein „overfitting“ des Modells zu vermeiden, wird neben dem Log-Likelihoodwert des Modells zusätzlich die Anzahl der Parameter als Summand in die Berechnung des Vergleichsmaßes integriert. | Das Akaike-Information-Criterion (AIC) wird zum Vergleich mehrerer Modelle basierend auf ihren Log-Likelihoodwerten verwendet. Je kleiner der AUC-Wert ist, umso besser ist der Fit des Modells. Der Log-Likelihoodwert ist umso größer, je besser das Modell die realen Daten vorhersagen kann. Um komplexere Modelle jedoch nicht grundsätzlich besser zu bewerten, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können und somit ein [[Auflösung vs. Noise|„overfitting“]] des Modells zu vermeiden, wird neben dem Log-Likelihoodwert des Modells zusätzlich die Anzahl der Parameter als Summand in die Berechnung des Vergleichsmaßes integriert. | ||
Die Ermittlung des AIC für ein Modell m erfolgt mithilfe folgender Formel: | |||
::[[Datei:Vergleichsmasse_1.png|link=Ausgelagerte_Formeln#AIC|Ausgelagerte Formel AIC]] | |||
::[[Datei:Vergleichsmasse_2.PNG|Das Bild ist Bestandteil der vorhergehenden Formel und wurde bereits dort beschrieben]] | |||
Bei der Berechnung des AIC ist zu beachten, dass es keinen vordefinierten Wertebereich gibt, welcher eine gute Anpassung des Modells an die Daten widerspiegelt. Der Wert an sich gibt also keine Auskunft über die Güte eines Modells. Deswegen eignet sich das AIC eher für den Vergleich zweier Modelle. Hierbei vergleicht man deren jeweilige AIC-Werte miteinander und entscheidet sich – falls es keine inhaltlichen Gründe gibt, die dagegensprechen – für das Modell mit dem geringeren AIC-Wert. | |||
== BIC == | |||
Das Bayesian-Information-Criterion (BIC) wird auch als Schwarz-Information-Criterion (SIC) bezeichnet und ähnelt dem AIC stark. Es wird ebenfalls zum Vergleich mehrerer Modelle basierend auf ihren Log-Likelihoodwerten verwendet. Wie beim AIC wird die Anzahl der Parameter auch hier bestrafend in die Berechnung des Informationskriteriums einbezogen. Zusätzlich wird diese aber noch mit der Anzahl der Beobachtungen multipliziert. | |||
Die Ermittlung des BIC für ein Modell m erfolgt mithilfe folgender Formel: | |||
::[[Datei:Vergleichsmasse_3.png|link=Ausgelagerte_Formeln#BIC|Ausgelagerte Formel BIC]] | |||
::[[Datei:Vergleichsmasse_4.PNG|Das Bild ist Bestandteil der vorhergehenden Formel und wurde bereits dort beschrieben]] | |||
Im Gegensatz zum AIC spielt beim BIC also die Stichprobengröße eine Rolle. Da große Stichproben eine Verbesserung des Log-Likelihoodwertes leichter ermöglichen, scheinen ohne deren Berücksichtigung Modelle mit verhältnismäßig vielen Parametern öfter als vorteilhaft. Durch Verwendung des BIC wird dieses Problem reduziert. Bereits ab einer Stichprobengröße von 8 (ln(8) = 2,07944 > 2) bestraft das BIC komplexere Modelle stärker als das AIC. | |||
Das bessere Modell besitzt den geringeren BIC Wert. Dieser kann jedoch, wie das AIC, nicht als absolutes Gütemaß verstanden werden. Auch ein Modell, welches mithilfe dieses Vergleichsmaßes als bestes Modell ermittelt wird, kann eine sehr schlechte Anpassung an die Daten aufweisen, da es lediglich besser ist, als die in den Vergleich einbezogenen Alternativmodelle. | |||
Aktuelle Version vom 9. Dezember 2021, 15:16 Uhr
Im Rahmen eines quantitativen Modellvergleichs wird die Balance zwischen möglichst geringer Parameteranzahl und guter Vorhersagefähigkeit verschiedener Modelle untersucht, um die Wahl eines optimalen Modells zu ermöglichen. Obwohl kein einheitliches Kriterium für diese Entscheidung existiert, kann die Berechnung von Vergleichsmaßen (auch als Informationskriterien bezeichnet) als Orientierung dienen. Diese Kriterien berücksichtigen nicht nur den Fit der Modelle an die empirischen Daten, sondern beachten zusätzlich die Anzahl der verwendeten Parameter. Dies ist wichtig, damit komplexere Modelle nicht grundsätzlich als besser eingestuft werden, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können. Das mit Hilfe der Vergleichsmaße ermittelte optimale Modell soll dabei das bestmögliche Verhältnis zwischen hoher Vorhersagefähigkeit und geringer Komplexität besitzen. Zu den am häufigsten verwendeten Vergleichsmaßen gehören das Akaike-Information-Criterion (AIC) und das Bayesian-Information-Criterion (BIC).
AIC
Das Akaike-Information-Criterion (AIC) wird zum Vergleich mehrerer Modelle basierend auf ihren Log-Likelihoodwerten verwendet. Je kleiner der AUC-Wert ist, umso besser ist der Fit des Modells. Der Log-Likelihoodwert ist umso größer, je besser das Modell die realen Daten vorhersagen kann. Um komplexere Modelle jedoch nicht grundsätzlich besser zu bewerten, weil sie exakter an die aktuell vorliegenden Daten angepasst werden können und somit ein „overfitting“ des Modells zu vermeiden, wird neben dem Log-Likelihoodwert des Modells zusätzlich die Anzahl der Parameter als Summand in die Berechnung des Vergleichsmaßes integriert.
Die Ermittlung des AIC für ein Modell m erfolgt mithilfe folgender Formel:
Bei der Berechnung des AIC ist zu beachten, dass es keinen vordefinierten Wertebereich gibt, welcher eine gute Anpassung des Modells an die Daten widerspiegelt. Der Wert an sich gibt also keine Auskunft über die Güte eines Modells. Deswegen eignet sich das AIC eher für den Vergleich zweier Modelle. Hierbei vergleicht man deren jeweilige AIC-Werte miteinander und entscheidet sich – falls es keine inhaltlichen Gründe gibt, die dagegensprechen – für das Modell mit dem geringeren AIC-Wert.
BIC
Das Bayesian-Information-Criterion (BIC) wird auch als Schwarz-Information-Criterion (SIC) bezeichnet und ähnelt dem AIC stark. Es wird ebenfalls zum Vergleich mehrerer Modelle basierend auf ihren Log-Likelihoodwerten verwendet. Wie beim AIC wird die Anzahl der Parameter auch hier bestrafend in die Berechnung des Informationskriteriums einbezogen. Zusätzlich wird diese aber noch mit der Anzahl der Beobachtungen multipliziert.
Die Ermittlung des BIC für ein Modell m erfolgt mithilfe folgender Formel:
Im Gegensatz zum AIC spielt beim BIC also die Stichprobengröße eine Rolle. Da große Stichproben eine Verbesserung des Log-Likelihoodwertes leichter ermöglichen, scheinen ohne deren Berücksichtigung Modelle mit verhältnismäßig vielen Parametern öfter als vorteilhaft. Durch Verwendung des BIC wird dieses Problem reduziert. Bereits ab einer Stichprobengröße von 8 (ln(8) = 2,07944 > 2) bestraft das BIC komplexere Modelle stärker als das AIC.
Das bessere Modell besitzt den geringeren BIC Wert. Dieser kann jedoch, wie das AIC, nicht als absolutes Gütemaß verstanden werden. Auch ein Modell, welches mithilfe dieses Vergleichsmaßes als bestes Modell ermittelt wird, kann eine sehr schlechte Anpassung an die Daten aufweisen, da es lediglich besser ist, als die in den Vergleich einbezogenen Alternativmodelle.