Komplexe Zahlen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Komplexe Zahlen sind eine Erweiterung der reellen Zahlen und bestehen aus einem realen und einem imaginären Anteil. Sie haben die Form ''a''+''bi'', wobei a der reale Teil und ''b'' der imaginäre Teil ist und i die imaginäre Einheit ist mit der Eigenschaft <math>i^{2} = -1</math>. Visuell kann man sich komplexe Zahlen als Vektoren auf der komplexen Zahlenebene vorstellen . Nebenbei bemerkt kann man jede Zahl als Vektor auf der Zahlenebene auffassen, nur dass Zahlen ohne imaginären Anteil Vektoren entlang der reellen Zahlenachse sind. | Komplexe Zahlen sind eine Erweiterung der reellen Zahlen und bestehen aus einem realen und einem imaginären Anteil. Sie haben die Form ''a''+''bi'', wobei a der reale Teil und ''b'' der imaginäre Teil ist und i die imaginäre Einheit ist mit der Eigenschaft <math>i^{2} = -1</math>. Visuell kann man sich komplexe Zahlen als Vektoren auf der komplexen Zahlenebene vorstellen . Nebenbei bemerkt kann man jede Zahl als Vektor auf der Zahlenebene auffassen, nur dass Zahlen ohne imaginären Anteil Vektoren entlang der reellen Zahlenachse sind. | ||
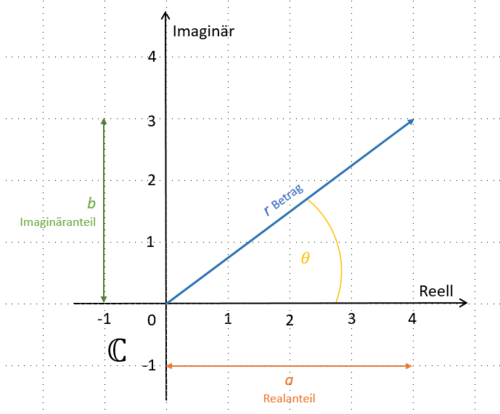
Wenn man komplexe Zahlen als Vektoren auffasst, lassen sie sich nicht nur durch ihre Koordinaten ausdrücken, sondern auch über ihren Betrag, also ihren Abstand zum Nullpunkt, und ihren Winkel zur positiven reellen Zahlenachse ( | Wenn man komplexe Zahlen als Vektoren auffasst, lassen sie sich nicht nur durch ihre Koordinaten ausdrücken, sondern auch über ihren Betrag, also ihren Abstand zum Nullpunkt, und ihren Winkel zur positiven reellen Zahlenachse (gegen den Uhrzeigersinn). Dieser Winkel wird auch das Argument der komplexen Zahl genannt. | ||
[[Datei:KomplexeZahlenebene.PNG|500px|zentriert]] | |||
''z'' sei eine beliebige komplexe Zahl. Dabei gilt: | ''z'' sei eine beliebige komplexe Zahl. Dabei gilt: | ||
| Zeile 8: | Zeile 10: | ||
<math>z = a \cdot bi </math> | <math>z = a \cdot bi </math> | ||
Betrag: <math>r = \mid z \mid = \sqrt{a^{2}+b^{2}}</math> | Betrag: <math>r = \mid z \mid = \sqrt{a^{2}+b^{2}}</math> (s. unten) | ||
Argument: <math>arg(z) = \Theta = arctan(\frac{b}{a})</math> | Argument: <math>arg(z) = \Theta = arctan(\frac{b}{a})</math> | ||
| Zeile 58: | Zeile 60: | ||
==Potenzen von ''i''== | ==Potenzen von ''i''== | ||
Potenzen von ''i'' verhalten sich wie folgt: | Potenzen von ''i'' verhalten sich wie folgt: <br> | ||
<math>i^{1} = i | <math>i^{1} = i</math> <br> | ||
<math>i^{2} = -1</math> <br> | |||
<math>i^{3} = -i</math> <br> | |||
<math>i^{4} = 1</math> <br> | |||
==Komplexe Exponentialfunktion== | ==Komplexe Exponentialfunktion== | ||
Die komplexe Exponentialfunktion, auch Eulersche Formel, ist definiert als: | Die komplexe Exponentialfunktion, auch Eulersche Formel, ist definiert als: | ||
<math>e^{ix} = cos(x) + i | <math>e^{ix} = cos(x) + i \cdot sin(x)</math> | ||
Die komplexe Exponentialfunktion ist auch wichtig für die Darstellung von periodischen Funktionen durch die Fourierreihe. Durch die Verwendung von komplexen Exponentialfunktionen können trigonometrische Reihen in kompakterer Form dargestellt werden. | Die komplexe Exponentialfunktion ist auch wichtig für die Darstellung von periodischen Funktionen durch die Fourierreihe. Durch die Verwendung von komplexen Exponentialfunktionen können trigonometrische Reihen in kompakterer Form dargestellt werden. | ||
| Zeile 70: | Zeile 75: | ||
=Komplexe Funktionen= | =Komplexe Funktionen= | ||
<math>f(z)= u(x,y) + iv(x,y)</math> | <math>f(z) = u(x,y) + iv(x,y)</math> | ||
Trigonometrische Form: | Trigonometrische Form: | ||
<math>f(z) = u( | <math>f(z) = u(r \cdot cos(\Theta),r \cdot sin(\Theta)) + i \cdot v \cdot (rcos(\Theta), r \cdot sin(\Theta))</math> | ||
Auch die komplexe Funktion ''f(z)'' besteht aus einem Realteil (''u'') und einem Imaginärteil (''v''). ''x'' und ''y'' werden in der trigonometrischen Form durch <math> | Auch die komplexe Funktion ''f(z)'' besteht aus einem Realteil (''u'') und einem Imaginärteil (''v''). ''x'' und ''y'' werden in der trigonometrischen Form durch <math>r \cdot cos(\Theta)</math> und <math>r \cdot sin(\Theta)</math> ersetzt. ''r'' ist dabei der Betrag der komplexen Zahl und Theta (<math>\Theta</math>) ihr Argument (s. oben). | ||
Aktuelle Version vom 19. August 2024, 13:40 Uhr
- Abbildungen folgen noch -
Komplexe Zahlen sind eine Erweiterung der reellen Zahlen und bestehen aus einem realen und einem imaginären Anteil. Sie haben die Form a+bi, wobei a der reale Teil und b der imaginäre Teil ist und i die imaginäre Einheit ist mit der Eigenschaft . Visuell kann man sich komplexe Zahlen als Vektoren auf der komplexen Zahlenebene vorstellen . Nebenbei bemerkt kann man jede Zahl als Vektor auf der Zahlenebene auffassen, nur dass Zahlen ohne imaginären Anteil Vektoren entlang der reellen Zahlenachse sind. Wenn man komplexe Zahlen als Vektoren auffasst, lassen sie sich nicht nur durch ihre Koordinaten ausdrücken, sondern auch über ihren Betrag, also ihren Abstand zum Nullpunkt, und ihren Winkel zur positiven reellen Zahlenachse (gegen den Uhrzeigersinn). Dieser Winkel wird auch das Argument der komplexen Zahl genannt.
z sei eine beliebige komplexe Zahl. Dabei gilt:
Betrag: (s. unten) Argument:
Man kann eine komplexe Zahl entsprechend auch durch ihren Betrag und ihr Argument darstellen, dabei spricht man von der Eulerschen Form bzw. der trigonometrischen Form:
Rechenregeln für komplexe Zahlen
Addition und Subtraktion
Bei Addition und Subtraktion betrachtet man die Real- und Imaginäranteile der Zahlen separat. Wenn man also die Zahlen und addieren oder subtrahieren möchte, werden die Realteile (a und c) und die Imaginärteile (bi und di) einzeln behandelt. Das sieht wie folgt aus:
Randnotiz: Die Klammern um bzw sind hier nicht notwendig und nur zur visuellen Verdeutlichung eingetragen. Im Fall von bzw. sind die Klammern notwendig, weil i ausgeklammert wurde.
Multiplikation
Für die Multiplikation komplexer Zahlen gilt das Distributivgesetz und wir müssen berücksichtigen, dass . Beispielsweise werden hier die Zahlen und multipliziert. Dabei löst man zuerst die Klammern unter Beachtung des Distributivgesetzes:
Dann wird durch −1 ersetzt:
Danach kann man zusammenfassen zu:
In der trigonometrischen Form:
Division
Um zwei komplexe Zahlen zu dividieren, multipliziert man den Zähler und den Nenner mit dem komplex konjugierten des Nenners und wendet dann die Regel für die Multiplikation an.
Komplex konjugierte: Das komplex konjugierte einer komplexen Zahl a+bi ist a−bi.
Betrag einer komplexen Zahl
Da komplexe Zahlen als Vektoren in der komplexen Zahlenebene anzusehen sind, kann man ihren Betrag (Länge des Vektors) mit dem Satz des Pythagoras berechnen. Dabei werden der Real- und der Imaginärteil als Katheten und der Betrag als Hypothenuse betrachtet. Dementsprechend berechnet sich der Betrag |z| einer komplexen Zahl wie folgt:
Potenzen von i
Potenzen von i verhalten sich wie folgt:
Komplexe Exponentialfunktion
Die komplexe Exponentialfunktion, auch Eulersche Formel, ist definiert als:
Die komplexe Exponentialfunktion ist auch wichtig für die Darstellung von periodischen Funktionen durch die Fourierreihe. Durch die Verwendung von komplexen Exponentialfunktionen können trigonometrische Reihen in kompakterer Form dargestellt werden.
Komplexe Funktionen
Trigonometrische Form:
Auch die komplexe Funktion f(z) besteht aus einem Realteil (u) und einem Imaginärteil (v). x und y werden in der trigonometrischen Form durch und ersetzt. r ist dabei der Betrag der komplexen Zahl und Theta () ihr Argument (s. oben).