Trigonometrie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen den Winkeln und Seitenlängen in Dreiecken beschäftigt. | Die Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen den Winkeln und Seitenlängen in Dreiecken beschäftigt. Diese Seite gibt eine kurze Einführung zu den wichtigsten Eckpunkten über trigonometrische Funktionen. Diese sind u.a. wichtig, um Verfahren von Signalverarbeitung zu verstehen (z.B. [[Konvolution|Konvolution]]). | ||
=Seitenverhältnisse= | =Seitenverhältnisse= | ||
Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben: | Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben: | ||
*'''Sinus:''' das Verhältnis der Länge von Gegenkathete zur Hypothenuse <math>sin(\beta) = \frac{a}{b}</math> | *'''Sinus:''' das Verhältnis der Länge von Gegenkathete zur Hypothenuse <math>\sin(\beta) = \frac{a}{b}</math> | ||
*'''Kosinus:''' das Verhältnis der Länge der Ankathete zur Hypotenuse <math>cos(\beta) = \frac{c}{b}</math> | *'''Kosinus:''' das Verhältnis der Länge der Ankathete zur Hypotenuse <math>\cos(\beta) = \frac{c}{b}</math> | ||
*'''Tangens:''' das Verhältnis der Länge der Gegenkathete zur Ankathete <math>tan(\beta) = \frac{c}{a}</math> | *'''Tangens:''' das Verhältnis der Länge der Gegenkathete zur Ankathete <math>\tan(\beta) = \frac{c}{a}</math> | ||
*'''Kotangens:''' das Reziprok des Tangens <math>cot(\beta) = \frac{a}{c}</math> | *'''Kotangens:''' das Reziprok des Tangens <math>\cot(\beta) = \frac{a}{c}</math> | ||
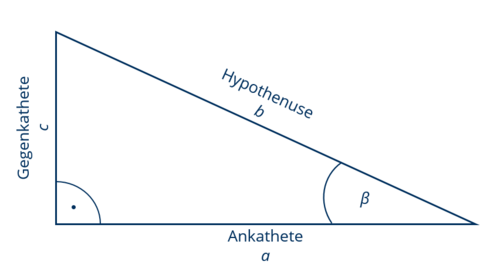
Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind. | Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind. Um die Winkel in Dreiecken zu berechnen, wenn die Seitenlängen bekannt sind, benötigt man die Umkehrfunktionen Arkussinus (<math>\sin^{-1}</math>), Arkuscosinus (<math>\cos^{-1}</math>) und Arkustangens(<math>\tan^{-1}</math>). | ||
[[Datei:TrigDreieck.PNG|500px|zentriert]] | [[Datei:TrigDreieck.PNG|500px|zentriert]] | ||
=Einheitskreis= | =Einheitskreis= | ||
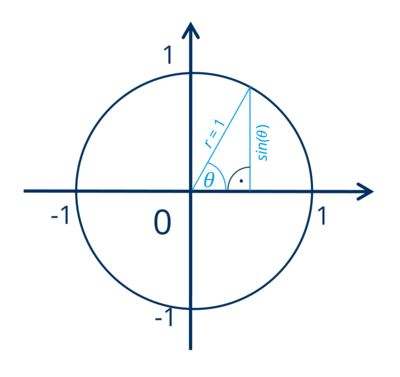
Der Einheitskreis ist ein Kreis mit einem Radius von 1, der seinen Mittelpunkt im Ursprung des Koordinatensystems (0,0) hat. Er ist ein wichtiges Werkzeug in der Trigonometrie, weil die Definitionen der trigonometrischen Funktionen Sinus und Kosinus auf ihm basieren können: Für einen Winkel <math>\theta</math> entspricht der Kosinus dem x-Koordinatenwert und der Sinus dem y-Koordinatenwert eines Punktes auf dem Einheitskreis. | Der Einheitskreis ist ein Kreis mit einem Radius von 1, der seinen Mittelpunkt im Ursprung des Koordinatensystems (0,0) hat. Er ist ein wichtiges Werkzeug in der Trigonometrie, weil die Definitionen der trigonometrischen Funktionen Sinus und Kosinus auf ihm basieren können: Für einen Winkel <math>\theta</math> entspricht der Kosinus dem x-Koordinatenwert und der Sinus dem y-Koordinatenwert eines Punktes auf dem Einheitskreis. Eine Erklärung mit Visualisierung haben [https://www.youtube.com/watch?v=fPPDVTVRnfY 3Blue1Brown] erstellt (Stand August 2024). | ||
[[Datei:Einheitskreis.PNG| | [[Datei:Einheitskreis.PNG|400px|zentriert]] | ||
=Funktionseigenschaften= | |||
==Periodizität & Frequenz== | |||
Wie im oben erwähnten Video ersichtlich, sind Sinus und Kosinus periodisch, das heißt, sie wiederholen sich in regelmäßigen Abständen. Die Zeit, bis eine Funktion einmal ihren Zyklus durchlaufen hat, ist die '''Periode'''. Der Sinus hat eine Periode von <math>2\pi</math>, das heißt <math>\sin(\theta + 2\pi) = \sin(\theta)</math>. Die Anzahl an Perioden, die die Funktion in einem festgelegten Intervall durchläuft ist ihre '''Frequenz'''. | |||
==Amplitude== | |||
Die Amplitude einer Funktion beschreibt die maximale Auslenkung oder den maximalen Abstand der Funktionswerte vom mittleren oder Ruhezustand (meist Nullpunkt) in einem Schwingungs- oder Wellenmuster. Im Kontext von periodischen Funktionen, wie z.B. Sinus- und Kosinusfunktionen, misst die Amplitude die Höhe der Welle vom mittleren Wert (der Achse) bis zum höchsten Punkt (Maximum) oder niedrigsten Punkt (Minimum) der Welle. Die Amplitude von \sin(\theta)</math>, wenn Theta ein Winkel eines Dreiecks auf dem Einheitskreis (wie oben beschrieben) ist, ist 1. | |||
==Phase== | |||
Die Phase einer Sinus- oder Kosinusfunktion beschreibt die horizontale Verschiebung der Welle entlang der ''x''-Achse. Sie gibt an, wie weit die Welle nach links oder rechts verschoben ist, relativ zu einer Referenzwelle. Sie wird häufig mit einem <math>\Phi</math> angegeben. Wenn <math>\Phi = 0</math>, beginnt der Sinus im Ursprung bei [0,0] und der Cosinus bei [0,1]. Zwei oder mehr Wellen können zueinander synchron oder phasenverschoben stehen. | |||
==Mathematische Darstellung== | |||
In der Beispielfunktion <math>f(x) = A \cdot \sin(\omega \cdot x + \Phi)</math> zeigt sich, wie die Funktionseigenschaften einer Sinusfunktion verändert werden können. Dabei sind die Größen wie folgt definiert: | |||
*A steht für die Amplitude, also die maximale Auslenkung der Sinuswelle. Ein Sinus ohne weitere Multiplikatoren hat die Amplitude 1. Ist die Amplitude negativ, wird der Sinusgraph an der ''x''-Achse gespiegelt. | |||
*<math>\Phi</math> steht für die Phase des Sinus. Bei einer Phase von <math>\Phi > 0</math> verschiebt sich der Sinusgraph nach links, bei <math>\Phi < 0</math> nach rechts entlang der ''x''-Achse | |||
*<math>\omega</math> steht für die Kreisfrequenz des Sinus, d.h. die Anzahl der Rotationen um den Einheitskreis in einem bestimmten Zeitintervall. Eine Rotation um den Einheitskreis ist eine Periode. Wenn man pro Zeitschritt mehr Rotationen macht, erhöht sich die Frequenz des Sinus bzw. die Periodenanzahl pro Zeitschritt. Dies drückt sich im Zusammenhang <math>\omega = \frac{2\pi}{T}</math> mit <math>T</math> als Periodenlänge aus. Wenn man also die Periodenlänge bzw. die Frequenz des Sinus verändern möchte, passt man <math>\omega</math> in der Gleichung oben an. Dabei verlängern <math>0 < |{\omega}| < 1</math> die Periode, d.h. die Frequenz wird kleiner. Wenn <math>|{\omega}| > 1</math>, wird die Periode kürzer, d.h. die Frequenz erhöht sich. | |||
Aktuelle Version vom 2. September 2024, 13:57 Uhr
Die Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen den Winkeln und Seitenlängen in Dreiecken beschäftigt. Diese Seite gibt eine kurze Einführung zu den wichtigsten Eckpunkten über trigonometrische Funktionen. Diese sind u.a. wichtig, um Verfahren von Signalverarbeitung zu verstehen (z.B. Konvolution).
Seitenverhältnisse
Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben:
- Sinus: das Verhältnis der Länge von Gegenkathete zur Hypothenuse
- Kosinus: das Verhältnis der Länge der Ankathete zur Hypotenuse
- Tangens: das Verhältnis der Länge der Gegenkathete zur Ankathete
- Kotangens: das Reziprok des Tangens
Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind. Um die Winkel in Dreiecken zu berechnen, wenn die Seitenlängen bekannt sind, benötigt man die Umkehrfunktionen Arkussinus (), Arkuscosinus () und Arkustangens().
Einheitskreis
Der Einheitskreis ist ein Kreis mit einem Radius von 1, der seinen Mittelpunkt im Ursprung des Koordinatensystems (0,0) hat. Er ist ein wichtiges Werkzeug in der Trigonometrie, weil die Definitionen der trigonometrischen Funktionen Sinus und Kosinus auf ihm basieren können: Für einen Winkel entspricht der Kosinus dem x-Koordinatenwert und der Sinus dem y-Koordinatenwert eines Punktes auf dem Einheitskreis. Eine Erklärung mit Visualisierung haben 3Blue1Brown erstellt (Stand August 2024).
Funktionseigenschaften
Periodizität & Frequenz
Wie im oben erwähnten Video ersichtlich, sind Sinus und Kosinus periodisch, das heißt, sie wiederholen sich in regelmäßigen Abständen. Die Zeit, bis eine Funktion einmal ihren Zyklus durchlaufen hat, ist die Periode. Der Sinus hat eine Periode von , das heißt . Die Anzahl an Perioden, die die Funktion in einem festgelegten Intervall durchläuft ist ihre Frequenz.
Amplitude
Die Amplitude einer Funktion beschreibt die maximale Auslenkung oder den maximalen Abstand der Funktionswerte vom mittleren oder Ruhezustand (meist Nullpunkt) in einem Schwingungs- oder Wellenmuster. Im Kontext von periodischen Funktionen, wie z.B. Sinus- und Kosinusfunktionen, misst die Amplitude die Höhe der Welle vom mittleren Wert (der Achse) bis zum höchsten Punkt (Maximum) oder niedrigsten Punkt (Minimum) der Welle. Die Amplitude von \sin(\theta)</math>, wenn Theta ein Winkel eines Dreiecks auf dem Einheitskreis (wie oben beschrieben) ist, ist 1.
Phase
Die Phase einer Sinus- oder Kosinusfunktion beschreibt die horizontale Verschiebung der Welle entlang der x-Achse. Sie gibt an, wie weit die Welle nach links oder rechts verschoben ist, relativ zu einer Referenzwelle. Sie wird häufig mit einem angegeben. Wenn , beginnt der Sinus im Ursprung bei [0,0] und der Cosinus bei [0,1]. Zwei oder mehr Wellen können zueinander synchron oder phasenverschoben stehen.
Mathematische Darstellung
In der Beispielfunktion zeigt sich, wie die Funktionseigenschaften einer Sinusfunktion verändert werden können. Dabei sind die Größen wie folgt definiert:
- A steht für die Amplitude, also die maximale Auslenkung der Sinuswelle. Ein Sinus ohne weitere Multiplikatoren hat die Amplitude 1. Ist die Amplitude negativ, wird der Sinusgraph an der x-Achse gespiegelt.
- steht für die Phase des Sinus. Bei einer Phase von verschiebt sich der Sinusgraph nach links, bei nach rechts entlang der x-Achse
- steht für die Kreisfrequenz des Sinus, d.h. die Anzahl der Rotationen um den Einheitskreis in einem bestimmten Zeitintervall. Eine Rotation um den Einheitskreis ist eine Periode. Wenn man pro Zeitschritt mehr Rotationen macht, erhöht sich die Frequenz des Sinus bzw. die Periodenanzahl pro Zeitschritt. Dies drückt sich im Zusammenhang mit als Periodenlänge aus. Wenn man also die Periodenlänge bzw. die Frequenz des Sinus verändern möchte, passt man in der Gleichung oben an. Dabei verlängern die Periode, d.h. die Frequenz wird kleiner. Wenn , wird die Periode kürzer, d.h. die Frequenz erhöht sich.