Wavelet-Transformation: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
[[Datei:Morlet.png|400px|zentriert]] | [[Datei:Morlet.png|400px|zentriert]] | ||
= | =Grundprinzip= | ||
Die Wavelet-Transformation ist wie folgt definiert:<br> | Die Wavelet-Transformation ist wie folgt definiert:<br> | ||
<math>W(a,b) = \int_{m=\infty}^{-\infty} x(t)\cdot \psi \cdot (\frac{t-b}{a}) dt </math> <br> | <math>W(a,b) = \int_{m=\infty}^{-\infty} x(t)\cdot \psi \cdot (\frac{t-b}{a}) dt </math> <br> | ||
| Zeile 18: | Zeile 18: | ||
*''b'' ist der Verschiebungsfaktor, also wi auf der ''x''-Achse das Wavelet positioniert wird | *''b'' ist der Verschiebungsfaktor, also wi auf der ''x''-Achse das Wavelet positioniert wird | ||
*für <math>\psi</math> setzt man die Funktion des Wavelets ein. Z.B. ist das Morlet-Wavelet definiert als: <math>\frac{1}{\sqrt{\sigma \sqrt{\pi}}} \exp\left(-\frac{t^2}{2\sigma^2}\right) \cos(2 \pi f_0 t)</math> | *für <math>\psi</math> setzt man die Funktion des Wavelets ein. Z.B. ist das Morlet-Wavelet definiert als: <math>\frac{1}{\sqrt{\sigma \sqrt{\pi}}} \exp\left(-\frac{t^2}{2\sigma^2}\right) \cos(2 \pi f_0 t)</math> | ||
**<math>\exp(x) = e^{x}</math> ist hier die Schreibweise der Exponentialfunktion mit der Basis ''e'' (Eulersche Zahl) und dem Exponenten ''x''. Im Morlet-Wavelet steht anstelle von ''x'' die Gaußsche Hüllkurve. | |||
Vereinfacht beschrieben, wird das Wavelet zuerst gestaucht oder gestreckt und dann über jeden Punkt eines Signals ''x''(''t'') geschoben und dort mit dem Signal gefaltet. Dabei erhält man den Wavelet-Koeffizienten, der angibt, wie stark das Signal an einer Stelle mit dem Wavelet übereinstimmt, d.h. wie stark die Schwingung des Wavelets im Signal vertreten ist. Dies wiederholt man über alle Punkte des Signals, um zu sehen, wie sich die Übereinstimmung über die Zeit hinweg verändert. Tut man das für verschiedene, unterschiedlich stark gestreckte Wavelets, erhält man diese Zeitreihe von Übereinstimmungen für verschiedene Frequenzanteile. <br> | |||
Wie auch bei der Fourier-Transformation kann man so sehen, wie sich die Frequenzkomponenten in einem Signal über die Zeit verändern. Dabei ist der Unterschied, dass man bei der Fouriertransformation mehrere Zeitintervalle betrachten muss, d.h. man erhält die Information über die Frequenzkomponenten eingeteilt in "Zeitfenster", während die Wavelet-Transformation die Zeitreihe der Frequenzkomponenten kontinuierlich abbilden kann. Damit kann man auch hier ein Sprektrogramm erstellen, wie es bereits im Artikel zur [[Fourier-Transformation|Fourier-Transformation]] erwähnt wurde. | |||
Aktuelle Version vom 2. September 2024, 14:40 Uhr
Die Wavelet-Transformation (WT) ist ein mathematisches Werkzeug, das verwendet wird, um Signale zu analysieren und zu verarbeiten. Im Gegensatz zur Fourier-Transformation, die Signale ausschließlich im Frequenzbereich analysiert, bietet die Wavelet-Transformation eine Analyse im Zeit-Frequenz-Bereich. Dies bedeutet, dass sie sowohl Informationen über die Frequenzen eines Signals als auch darüber, wann diese Frequenzen auftreten, liefert.
Wavelet
Ein Wavelet (frz. "kleine Welle") ist eine kleine, oszillierende Wellenform, die sowohl in der Zeit (oder im Raum) als auch in der Frequenz begrenzt ist. Sie haben folgende Eigenschaften:
- Lokalisierung in Zeit und Frequenz: Ein Wavelet ist sowohl in der Zeit (oder im Raum) als auch in der Frequenz begrenzt. Dies bedeutet, dass ein Wavelet nur für eine kurze Dauer eine nicht-null Amplitude hat (es ist zeitlich begrenzt) und dass es nur eine bestimmte Bandbreite an Frequenzen enthält (es ist auch frequenzmäßig begrenzt).
- Nullmittelwert: Ein Wavelet hat in der Regel einen Nullmittelwert, was bedeutet, dass positive und negative Ausschläge sich im Durchschnitt ausgleichen.
- Skalierbarkeit & Verschiebung: Ein Wavelet kann skaliert (gestreckt oder gestaucht) und verschoben werden. Diese Eigenschaften erlauben es, ein Signal in verschiedenen Auflösungen und zu unterschiedlichen Zeitpunkten zu analysieren.
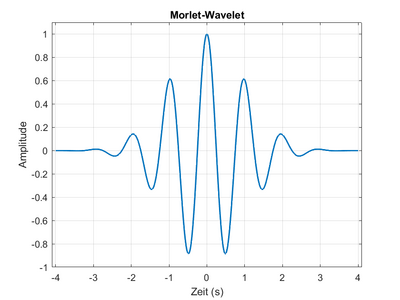
Das bedeutet, dass Wavelets sowohl in der Lage sind, kurze, hochfrequente Signalmerkmale als auch langanhaltende, niederfrequente Signalmerkmale zu erfassen. Sie werden durch Skalierung (Ändern der Breite) und Verschiebung (Ändern der Position) eines sogenannten "Mutter-Wavelets" erzeugt. Diese Skalierung und Verschiebung ermöglichen es, das Signal auf verschiedenen Auflösungsstufen zu analysieren. Es gibt viele Arten von Wavelets, die jeweils unterschiedlich geformt sind, um für verschiedene Anwendungen besonders nützlich zu sein. Im der Abbildung ist beispielhaft ein Morlet-Wavelet mit der zentralen Frequenz und Standardabweichung im Zeitintervall [-4,4] gezeigt. Ein [Morlet-Wavelet (engl. Wikipedia, Stand August 2024) ist eine spezielle Art von Wavelet, das durch die Kombination einer Sinuswelle und einer Gaußschen Hüllkurve definiert ist.
Grundprinzip
Die Wavelet-Transformation ist wie folgt definiert:
Die Größen in der Formel sind wie folgt definiert:
- W(a,b) ist der Wavelet-Koeffizient für die Skala a und Verschiebung b
- a ist der Skalierungsfaktor, also wie stark das Wavelet gestreckt/gestaucht wird
- b ist der Verschiebungsfaktor, also wi auf der x-Achse das Wavelet positioniert wird
- für setzt man die Funktion des Wavelets ein. Z.B. ist das Morlet-Wavelet definiert als:
- ist hier die Schreibweise der Exponentialfunktion mit der Basis e (Eulersche Zahl) und dem Exponenten x. Im Morlet-Wavelet steht anstelle von x die Gaußsche Hüllkurve.
Vereinfacht beschrieben, wird das Wavelet zuerst gestaucht oder gestreckt und dann über jeden Punkt eines Signals x(t) geschoben und dort mit dem Signal gefaltet. Dabei erhält man den Wavelet-Koeffizienten, der angibt, wie stark das Signal an einer Stelle mit dem Wavelet übereinstimmt, d.h. wie stark die Schwingung des Wavelets im Signal vertreten ist. Dies wiederholt man über alle Punkte des Signals, um zu sehen, wie sich die Übereinstimmung über die Zeit hinweg verändert. Tut man das für verschiedene, unterschiedlich stark gestreckte Wavelets, erhält man diese Zeitreihe von Übereinstimmungen für verschiedene Frequenzanteile.
Wie auch bei der Fourier-Transformation kann man so sehen, wie sich die Frequenzkomponenten in einem Signal über die Zeit verändern. Dabei ist der Unterschied, dass man bei der Fouriertransformation mehrere Zeitintervalle betrachten muss, d.h. man erhält die Information über die Frequenzkomponenten eingeteilt in "Zeitfenster", während die Wavelet-Transformation die Zeitreihe der Frequenzkomponenten kontinuierlich abbilden kann. Damit kann man auch hier ein Sprektrogramm erstellen, wie es bereits im Artikel zur Fourier-Transformation erwähnt wurde.