Perzeptron: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) (→Das XOR-Problem: link einfügen pb) |
||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Neuronale Netze|Kognitive Modellierung|Hauptseite}} | ||
Das von Frank Rosenblatt im Jahre 1958 erfundene Perzeptron bildet die Grundlage heutiger künstlicher [[Neuronale Netze|neuronaler Netze]]. In seiner ursprünglichen Version besteht es aus einem einzelnen Knoten. Die Bezeichnung „Perzeptron“ gilt daher sowohl für einen einzelnen Knoten als auch für ein- oder mehrschichtige Netze aus diesen Knoten. | Das von Frank Rosenblatt im Jahre 1958 erfundene Perzeptron bildet die Grundlage heutiger künstlicher [[Neuronale Netze|neuronaler Netze]]. In seiner ursprünglichen Version besteht es aus einem einzelnen Knoten. Die Bezeichnung „Perzeptron“ gilt daher sowohl für einen einzelnen Knoten als auch für ein- oder mehrschichtige Netze aus diesen Knoten. | ||
| Zeile 10: | Zeile 8: | ||
== Lernen im Perzeptron == | == Lernen im Perzeptron == | ||
Das Perzeptron kann lernen, Inputmuster einer Kategorie zuzuordnen. Bei binärem Output funktioniert das Lernen wie folgt. Stimmt der Output mit dem gewünschten Wert überein, findet keine Gewichtsänderung statt. Ist der Output 0, obwohl 1 gewünscht ist, wird eine Vergrößerung der Gewichte vorgenommen. Bei einem Output von 1, der eigentlich 0 sein sollte, werden die Gewichte verringert. Diese Perzeptron-Lernregel ist eine Form der [[ | Das Perzeptron kann lernen, Inputmuster einer Kategorie zuzuordnen. Bei binärem Output funktioniert das Lernen wie folgt. Stimmt der Output mit dem gewünschten Wert überein, findet keine Gewichtsänderung statt. Ist der Output 0, obwohl 1 gewünscht ist, wird eine Vergrößerung der Gewichte vorgenommen. Bei einem Output von 1, der eigentlich 0 sein sollte, werden die Gewichte verringert. Diese Perzeptron-Lernregel ist eine Form der [[Deltaregel]]. Andere Lernregeln können ebenfalls implementiert werden, so zum Beispiel das [[Unsupervised: Hebb|Hebb’sche Lernen]]. | ||
== Das XOR-Problem == | == Das XOR-Problem == | ||
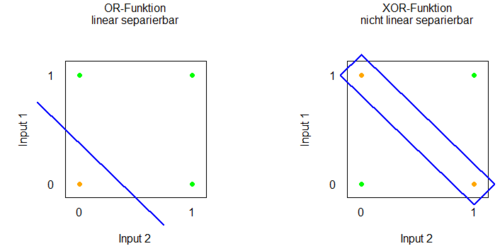
Ein einschichtiges Perzeptron kann viele Kategorisierungsregeln lernen, jedoch wird vorausgesetzt, dass die Inputmuster in der Regel linear separierbar sind. Was bedeutet das? Nehmen wir als Beispiel an, das Perzeptron erhält zwei Inputs, die jeweils an oder aus sein können. Dies können wir als 2-dimensionales Koordinatensystem darstellen (siehe Grafik), in dem jede Achse einen Input repräsentiert. In diesem Koordinatensystem können wir nun verschiedene Kategorisierungsregeln betrachten. Eine OR-Kategorisierungsregel sagt beispielsweise, dass das Perzeptron feuern soll, wenn mindestens einer der beiden Inputs 1 ist. Wenn kein Input 1 ist, soll das Perzeptron inaktiv bleiben. Diese Kategorisierung ist durch den Schwellwert möglich. In unserem Koordinatensystem stellt diesen Schwellwert eine Linie dar, die den Raum der möglichen Kategorisierungen in 2 Bereiche teilt: einen, in dem das Perzeptron feuern soll, und einen, in dem es nicht feuern soll. Da die Bereiche durch eine gerade Linie getrennt sind, sind sie linear separierbar. Ein Problem stellt die XOR-Kategorisierungsregel (exklusives Oder) dar. Eine XOR-Regel fordert, dass das Perzeptron feuern soll, wenn genau einer der beiden Inputs 1 ist, nicht aber bei beiden gleichzeitig. Diese Separierung ist nun nicht einfach durch eine Linie durchführbar. An dieser Stelle scheitert das einfache Perzeptron. | Ein einschichtiges Perzeptron kann viele Kategorisierungsregeln lernen, jedoch wird vorausgesetzt, dass die Inputmuster in der Regel linear separierbar sind. Was bedeutet das? Nehmen wir als Beispiel an, das Perzeptron erhält zwei Inputs, die jeweils an oder aus sein können. Dies können wir als 2-dimensionales Koordinatensystem darstellen (siehe Grafik), in dem jede Achse einen Input repräsentiert. In diesem Koordinatensystem können wir nun verschiedene Kategorisierungsregeln betrachten. Eine OR-Kategorisierungsregel sagt beispielsweise, dass das Perzeptron feuern soll, wenn mindestens einer der beiden Inputs 1 ist. Wenn kein Input 1 ist, soll das Perzeptron inaktiv bleiben. Diese Kategorisierung ist durch den Schwellwert möglich. In unserem Koordinatensystem stellt diesen Schwellwert eine Linie dar, die den Raum der möglichen Kategorisierungen in 2 Bereiche teilt: einen, in dem das Perzeptron feuern soll, und einen, in dem es nicht feuern soll. Da die Bereiche durch eine gerade Linie getrennt sind, sind sie linear separierbar. Ein Problem stellt die XOR-Kategorisierungsregel (exklusives Oder) dar. Eine XOR-Regel fordert, dass das Perzeptron feuern soll, wenn genau einer der beiden Inputs 1 ist, nicht aber bei beiden gleichzeitig. Diese Separierung ist nun nicht einfach durch eine Linie durchführbar. An dieser Stelle scheitert das einfache Perzeptron. | ||
[[Datei:Lineare_separierbarkeit.PNG|500px|link=Ausgelagerte_Bildbeschreibungen#XOR|Ausgelagerte Bildbeschreibung von XOR]] | |||
[[ | Der Nachweis dieses Scheiterns führte damals zu einer Krise in der Forschung zu neuronalen Netzen, denn die Lösung des Problems bestand in der Verwendung eines mehrschichtigen Perzeptrons, auf dass sich aber die allseits verwendete [[Deltaregel|Delta-Lernregel]] nicht anwenden ließ. Erst die Erfindung der [[Backpropagation]]-Lernregel löste dieses Problem und läutete damit eine neue Blüte der [[Neuronale Netze|neuronalen Netze]] ein. | ||
Aktuelle Version vom 18. Januar 2022, 12:54 Uhr
Das von Frank Rosenblatt im Jahre 1958 erfundene Perzeptron bildet die Grundlage heutiger künstlicher neuronaler Netze. In seiner ursprünglichen Version besteht es aus einem einzelnen Knoten. Die Bezeichnung „Perzeptron“ gilt daher sowohl für einen einzelnen Knoten als auch für ein- oder mehrschichtige Netze aus diesen Knoten.
Aufbau eines Perzeptrons
Das Perzeptron wandelt einen Input in einen Output um. Der Input besteht aus einem Vektor, von dem jeder Wert eine bestimmte Gewichtung besitzt. Um den Netzinput zu ermittelt, werden alle Werte mit den Gewichten multipliziert und aufsummiert. Danach kommt eine Aktivierungsfunktion ins Spiel, die dem Netzinput einen Output zuordnet. Dabei handelt es sich beim traditionellen Perzeptron um eine Stufenfunktion, da ein strikter Schwellwert gilt. Liegt der Netzinput über diesem Wert, feuert das Perzeptron, das heißt, es erhält den Wert 1. Andernfalls ist es inaktiv und besitzt den Wert 0. Darüber hinaus ist es auch möglich, durch eine andere Aktivierungsfunktion einen nichtbinären Output zu erzielen.
Lernen im Perzeptron
Das Perzeptron kann lernen, Inputmuster einer Kategorie zuzuordnen. Bei binärem Output funktioniert das Lernen wie folgt. Stimmt der Output mit dem gewünschten Wert überein, findet keine Gewichtsänderung statt. Ist der Output 0, obwohl 1 gewünscht ist, wird eine Vergrößerung der Gewichte vorgenommen. Bei einem Output von 1, der eigentlich 0 sein sollte, werden die Gewichte verringert. Diese Perzeptron-Lernregel ist eine Form der Deltaregel. Andere Lernregeln können ebenfalls implementiert werden, so zum Beispiel das Hebb’sche Lernen.
Das XOR-Problem
Ein einschichtiges Perzeptron kann viele Kategorisierungsregeln lernen, jedoch wird vorausgesetzt, dass die Inputmuster in der Regel linear separierbar sind. Was bedeutet das? Nehmen wir als Beispiel an, das Perzeptron erhält zwei Inputs, die jeweils an oder aus sein können. Dies können wir als 2-dimensionales Koordinatensystem darstellen (siehe Grafik), in dem jede Achse einen Input repräsentiert. In diesem Koordinatensystem können wir nun verschiedene Kategorisierungsregeln betrachten. Eine OR-Kategorisierungsregel sagt beispielsweise, dass das Perzeptron feuern soll, wenn mindestens einer der beiden Inputs 1 ist. Wenn kein Input 1 ist, soll das Perzeptron inaktiv bleiben. Diese Kategorisierung ist durch den Schwellwert möglich. In unserem Koordinatensystem stellt diesen Schwellwert eine Linie dar, die den Raum der möglichen Kategorisierungen in 2 Bereiche teilt: einen, in dem das Perzeptron feuern soll, und einen, in dem es nicht feuern soll. Da die Bereiche durch eine gerade Linie getrennt sind, sind sie linear separierbar. Ein Problem stellt die XOR-Kategorisierungsregel (exklusives Oder) dar. Eine XOR-Regel fordert, dass das Perzeptron feuern soll, wenn genau einer der beiden Inputs 1 ist, nicht aber bei beiden gleichzeitig. Diese Separierung ist nun nicht einfach durch eine Linie durchführbar. An dieser Stelle scheitert das einfache Perzeptron.
Der Nachweis dieses Scheiterns führte damals zu einer Krise in der Forschung zu neuronalen Netzen, denn die Lösung des Problems bestand in der Verwendung eines mehrschichtigen Perzeptrons, auf dass sich aber die allseits verwendete Delta-Lernregel nicht anwenden ließ. Erst die Erfindung der Backpropagation-Lernregel löste dieses Problem und läutete damit eine neue Blüte der neuronalen Netze ein.