Der p-Wert

Der p-Wert ist die zentrale Größe beim Testen statistischer Hypothesen. Er gibt an, wie wahrscheinlich es unter Gültigkeit der Nullhypothese ist, den in einer Stichprobe berechneten Schätzwert, oder einen der Nullhypothese noch mehr widersprechenden Wert zu erhalten. Je geringer der p-Wert, desto eher kann die Nullhypothese für die vorliegende Population ablehnt werden. Ist der p-Wert geringer als das vorher festgelegte Signifikanzniveau α, wird das Ergebnis als signifikant bezeichnet und die Nullhypothese abgelehnt. Das Signifikanzniveau wird in der Praxis zumeist auf α = 0.05 oder α = 0.01 festgelegt. Die Größe des p-Wertes ist abhängig von der Art der Fragestellung. Dabei wird zwischen gerichteten (einseitigen) und ungerichteten (zweiseitigen) Fragestellungen unterschieden. Will man z.B. nachweisen, dass sich die Werte einer Stichprobe im Persönlichkeitsmerkmal Neurotizismus von den Werten in der Grundgesamtheit unterscheiden, liegt eine zweiseitige Fragestellung vor. Die zweiseitige Fragestellung trifft keine Aussage über die Richtung des Unterschiedes. Will man jedoch nachweisen, dass die Neurotizismus-Ausprägungen in der Stichprobe höher sind als in der Grundgesamtheit, so handelt es sich um eine einseitige Fragestellung.

Beispiel

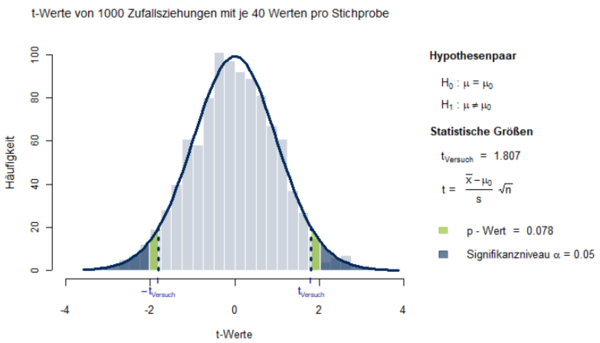
In einem fiktiven Beispiel wurde in einer Stichprobe von Psychologiestudierenden der Größe n = 40 der Mittelwert von x̅ = 23 bei einer Standardabweichung von s = 7 in Neurotizismus erfasst. Der bekannte Mittelwert in der Grundgesamtheit der Allgemeinbevölkerung beträgt µ₀ = 21. Bei einer zweiseitigen Fragestellung drückt die Alternativhypothese aus, dass sich der Populationsmittelwert der Psychologiestudierenden vom Mittelwert der Allgemeinbevölkerung unterscheidet (H₁: µ_P ≠ µ₀). Die Nullhypothese drückt komplementär dazu aus, dass sich die Mittelwerte der Grundgesamtheiten nicht voneinander unterscheiden (H₀: µ_P = µ₀). Ein zweiseitiger t-Test ergibt einen t-Wert von t(39) = 1.807 und einen p-Wert von p = 0.078. Die Wahrscheinlichkeit, den in der Stichprobe berechneten Schätzwert x̅ = 23 oder einen betragsmäßig noch stärker von µ₀ = 21 abweichenden Mittelwert bei einer Standardabweichung s = 7 unter der Annahme der Nullhypothese zu erhalten, beträgt 7,8 Prozent. Bei einem Signifikanzniveau von α = 0.05 ist der gefundene Mittelwertsunterschied wegen 0.078 > 0.05 nicht signifikant. In Abbildung 1 ist dieser Sachverhalt mithilfe der interaktiven Simulation zum p-Wert grafisch veranschaulicht.

kkk Im Video wird der p-Wert bei zweiseitiger Fragestellung näher erläutert.

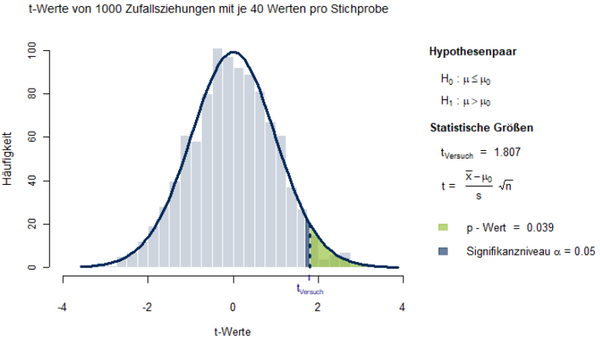
Bei einer einseitigen Fragestellung wird die Alternativhypothese untersucht, dass der Populationsmittelwert in Neurotizismus in der Grundgesamtheit der Psychologiestudierenden größer ist als der Mittelwert der Allgemeinbevölkerung (H₁: µ_P > µ_0). Die Nullhypothese besagt dazu komplementär, dass der Mittelwert in der Grundgesamtheit mindestens genauso hoch oder höher ist als der Mittelwert der Grundgesamtheit der Psychologiestudierenden (H₀: µ_P ≤ µ₀). Unter ansonsten gleichen Bedingungen ergibt sich hier der halbierte p-Wert von p = 0.039. Die Wahrscheinlichkeit, den in der Stichprobe berechneten Schätzwert x̅ = 23, oder einen noch größeren Schätzwert unter Annahme der Nullhypothese zu erhalten, liegt bei 3,9 Prozent. Bei einem Signifikanzniveau von α = 0.05 ist der gefundene Mittelwertsunterschied wegen 0.039 < 0.05 signifikant. In Abbildung 2 ist der einseitige p-Wert dieses Beispiels grafisch veranschaulicht.

kkk Im Video wird der p-Wert bei einseitiger Fragestellung näher erläutert.

kkk Inwieweit der p-Wert von verschiedenen Parametern abhängig ist, lässt sich in der interaktiven Simulation nachvollziehen.

Weiterführende Literatur

Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 5.3). München: Pearson Studium.