Teststärke: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 16: | Zeile 16: | ||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_4_Teststaerke_Link.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_4_Teststaerke_Link.html Video] wird die Teststärke näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_4_Teststaerke/ | ||
|120px]] <span style="color: white"> kkk </span> Wie die Teststärke von verschiedenen Parametern abhängig ist, lässt sich in der [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Wie die Teststärke von verschiedenen Parametern abhängig ist, lässt sich in der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_4_Teststaerke/ interaktiven Simulation] grafisch veranschaulichen. | ||
Version vom 16. März 2020, 09:47 Uhr
Die Teststärke (engl. Power), auch Güte oder Macht genannt, bezeichnet in der Testtheorie die Wahrscheinlichkeit die Nullhypothese korrekterweise abzulehnen, wenn die Alternativhypothese in der Grundgesamtheit gilt. In der Praxis spielt die Teststärke z.B. bei der Stichprobenumfangsplanung eine wichtige Rolle. Die Teststärke entspricht der Wahrscheinlichkeit, keinen Fehler 2. Art (β) zu machen und lässt sich dementsprechend als Gegenwahrscheinlichkeit 1-β darstellen. Ein Fehler 2. Art beschreibt entsprechend die Wahrscheinlichkeit, die Nullhypothese fälschlicherweise beizubehalten, obwohl die Alternativhypothese gültig ist. Anders als die Wahrscheinlichkeit eines Fehlers 1. Art, die durch das Signifikanzniveau α vom Anwender festgelegt wird, variiert die Wahrscheinlichkeit eines Fehlers 2. Art und damit auch die Teststärke in Abhängigkeit verschiedener Kenngrößen. Zum einen steigt die Teststärke bei geringeren Streuungen in den Grundgesamtheiten. Zum anderen wird die Teststärke durch die Effektgröße mitbestimmt: Gibt es einen großen Effekt, also einen größeren Mittelwertsunterschied zwischen zwei Grundgesamtheiten, ist die Teststärke höher. Sowohl die Streuung als auch der Mittelwertsunterschied der Grundgesamtheiten sind in der Praxis jedoch feste Größen und können vom Anwender nicht variiert werden. Um dennoch positiven Einfluss auf die Teststärke zu nehmen, kann z.B. ein liberaleres Signifikanzniveau α (z.B. 0.05 statt 0.01) festgelegt werden. Dadurch würde sich jedoch die Wahrscheinlichkeit eines Fehlers 1. Art erhöhen. Eine praktisch sehr wichtige Methode zur Erhöhung der Teststärke ist die Vergrößerung des Stichprobenumfangs n. Inwieweit der Stichprobenumfang einen Einfluss auf die Teststärke hat, wird in dem Text zur Stichprobenumfangsplanung ausführlich beschrieben.
Beispiel
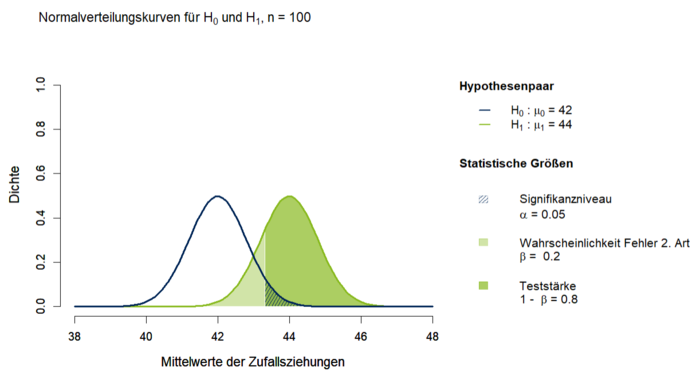
In einer fiktiven Studie wird in einer Oberschule ein neues Trainingsprogramm für die Verbesserung der Matheleistungen implementiert. Zusätzlich zum Matheunterricht rechnen 100 Schüler für 3 Monate wöchentlich unter Aufsicht eine Stunde Matheübungen. Um die Wirkung des Trainings zu überprüfen, führen die Schüler am Ende der Übungsphase einen Test durch. Es ist bekannt, dass Schüler dieser Altersklasse in diesem Test im Mittel µ0 = 42 Punkte bei einer Standardabweichung von σ = 8 erzielen. Die Lehrer, die dieses Trainingsprogramm ins Leben gerufen haben, sind nun interessiert daran, wie wahrscheinlich es ist, dass sie bei einem Signifikanzniveau von α = 0.05 ein signifikantes Ergebnis finden, wenn das Trainingsprogramm die mittleren Leistungen der Schüler um 2 Punkte auf µ1 = 44 bei gleichbleibender Standardabweichung erhöht. Dafür werden die Verteilungen der Nullhypothese µ0 = 42 und der Alternativhypothese µ1 = 44 jeweils mit n = 100 und σ = 8 simuliert und unter Annahme der Gültigkeit der Nullhypothese miteinander verglichen. In Abbildung 1 wird dieser Sachverhalt grafisch dargestellt.
Es zeigt sich, dass unter den vorliegenden Parametern die Wahrscheinlichkeit eines Fehlers 2. Art bei 20 % liegt. Das heißt wenn das Training die Leistungen der Schüler um zwei Punkte verbessert, besteht eine Wahrscheinlichkeit von 20 %, dass fälschlicherweise kein Effekt des Trainings in den Daten gefunden wird, obwohl die Alternativhypothese gilt. Die Teststärke beträgt 80%. Mit einer Wahrscheinlichkeit von 80 % wird also bei den vorliegenden Parametern ein signifikanter Effekt gefunden, wenn auch tatsächlich ein signifikanter Effekt vorliegt.
kkk Im Video wird die Teststärke näher erläutert.
kkk Wie die Teststärke von verschiedenen Parametern abhängig ist, lässt sich in der interaktiven Simulation grafisch veranschaulichen.
Weiterführende Literatur
Cohen, J. (2013). Statistical power analysis for the behavioral sciences. Routledge.
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 9.3). München: Pearson Studium.