Neuronale Netze: Unterschied zwischen den Versionen
Elisa (Diskussion | Beiträge) |
Elisa (Diskussion | Beiträge) |
||
| Zeile 9: | Zeile 9: | ||
== Funktionsweise eines Knotens == | == Funktionsweise eines Knotens == | ||
[[File:Netzinput_Neuron.png||600px|link=Ausgelagerte_Bildbeschreibungen# | [[File:Netzinput_Neuron.png||600px|link=Ausgelagerte_Bildbeschreibungen#Funktionsweise_eines_Knotens|Ausgelagerte Bildbeschreibung von Funktionsweise eines Knotens]] | ||
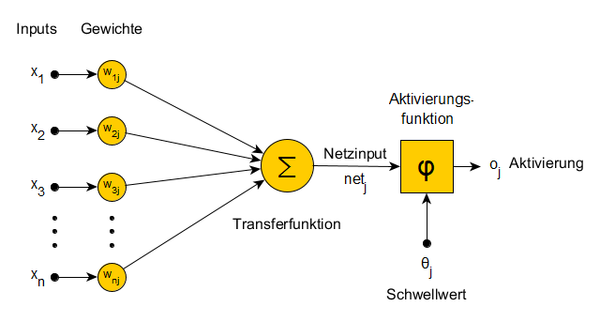
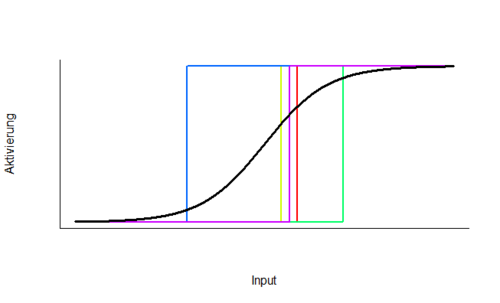
Knoten sind als simulierte Neurone kleine Recheneinheiten. Sie wandeln einen Input ''x'' in einen Output ''o'' um. Der Input ist ein Vektor aus Aktivierungsstärken oder Feuerraten. Dieser wird an den simulierten Synapsen gewichtet und schließlich aufsummiert, sodass ein einzelner Wert, der Netzinput, übrigbleibt. Um aus diesem die Outputaktivierung zu berechnen, wird eine Aktivierungsfunktion zwischengeschaltet, welche jedem Netzinput eine Outputstärke zuordnet. Dies kann zum Beispiel eine lineare Funktion, eine Sigmoidfunktion oder eine Schwellwertfunktion sein. Eine Schwellwertfunktion implementiert die Aktivierungsschwelle, die jedes einzelne natürliche Neuron auszeichnet. Bis zu einer bestimmten Inputstärke bleibt das Neuron inaktiv, bei darüber hinausgehendem Input entwickelt es ein Aktionspotential, es „feuert“. Dieser Schwellwert ist für jedes Neuron individuell und variiert über Neuone hinweg. An dieser Stelle ist es wichtig, das Knoten in Netzen oftmals nicht einzelne Neurone simulieren, sondern eigentlich viele Neurone, sogenannte Neuronenverbände (neural assemblies). Entsprechend unscharf wird die Aktivierungsschwelle des gesamten Knotens, denn einige Neurone feuern leichter und einige schwerer. Eine Sigmoidfunktion fasst diese individuellen Schwellwerte zusammen, indem sie die Aktivierungsstärke nicht mehr sprungartig, sondern soft, abhängig von der Anzahl der bereits feuernden Neurone, abbildet. Daher wird diese Aktivierungsfunktion oft für die Simulation biologischer Neuronenverbände verwendet. | Knoten sind als simulierte Neurone kleine Recheneinheiten. Sie wandeln einen Input ''x'' in einen Output ''o'' um. Der Input ist ein Vektor aus Aktivierungsstärken oder Feuerraten. Dieser wird an den simulierten Synapsen gewichtet und schließlich aufsummiert, sodass ein einzelner Wert, der Netzinput, übrigbleibt. Um aus diesem die Outputaktivierung zu berechnen, wird eine Aktivierungsfunktion zwischengeschaltet, welche jedem Netzinput eine Outputstärke zuordnet. Dies kann zum Beispiel eine lineare Funktion, eine Sigmoidfunktion oder eine Schwellwertfunktion sein. Eine Schwellwertfunktion implementiert die Aktivierungsschwelle, die jedes einzelne natürliche Neuron auszeichnet. Bis zu einer bestimmten Inputstärke bleibt das Neuron inaktiv, bei darüber hinausgehendem Input entwickelt es ein Aktionspotential, es „feuert“. Dieser Schwellwert ist für jedes Neuron individuell und variiert über Neuone hinweg. An dieser Stelle ist es wichtig, das Knoten in Netzen oftmals nicht einzelne Neurone simulieren, sondern eigentlich viele Neurone, sogenannte Neuronenverbände (neural assemblies). Entsprechend unscharf wird die Aktivierungsschwelle des gesamten Knotens, denn einige Neurone feuern leichter und einige schwerer. Eine Sigmoidfunktion fasst diese individuellen Schwellwerte zusammen, indem sie die Aktivierungsstärke nicht mehr sprungartig, sondern soft, abhängig von der Anzahl der bereits feuernden Neurone, abbildet. Daher wird diese Aktivierungsfunktion oft für die Simulation biologischer Neuronenverbände verwendet. | ||
Version vom 14. Januar 2022, 15:26 Uhr
Künstliche neuronale Netze, die in der Psychologie auch als konnektionistische Modelle bezeichnet werden, sind Modelle, deren Entwicklung ursprünglich durch das biologische Vorbild natürlicher Neurone inspiriert wurde. Die wohl grundlegendste Gemeinsamkeit zum Gehirn liegt in der Fähigkeit zu lernen. So könnte zum Beispiel ein künstliches neuronales Netz ebenso wie der Mensch ein ihm bekanntes Bild einer Katze wiedererkennen (im Sinne von richtig zuordnen). Darüber hinaus sind beide Systeme in der Lage, über Bekanntes hinaus zu generalisieren. Ein Kind, welches bisher nur seine gefleckte Hauskatze kannte, kann auch die einfarbige Katze des Nachbarn auf den ersten Blick als Katze einordnen. Hier spielt auch die Fähigkeit zur Mustererkennung eine Rolle. Sowohl Menschen als auch neuronale Netzwerke können Regelmäßigkeiten in Daten erkennen, so zum Beispiel, dass alle Katzen vier Beine haben. Sollten gerade nur drei davon zu sehen sein – kein Problem. Das Gehirn ist tolerant gegenüber Fehlern wie unvollständigem oder verrauschtem Input, sodass die Katze trotzdem erkannt wird. Auch diese Fähigkeit des Gehirns imitieren künstliche neuronale Netze. Aufgrund ihrer funktionellen Ähnlichkeit mit dem Gehirn liefern neuronale Netze ein Modell zur Erklärung von Funktionen wie Lernen und Gedächtnis. Außerdem werden sie genutzt, um (nicht nur kognitive) Phänomene zu replizieren und vorherzusagen.
Aufbau von Netzwerkmodellen
Angelehnt an die neuronale Struktur des Gehirns bestehen künstliche neuronale Netze aus miteinander verknüpften Knoten, die simulierten Neuronen bzw. Verbänden von Neuronen, sogenannten Assemblies, entsprechen. Die Knoten kommunizieren miteinander über gewichtete Verbindungen, welche simulierten Synapsen entsprechen. Der Einfluss von Knoten aufeinander hängt von der Stärke ihrer Verbindung ab. Verbindungen können ein positives oder ein negatives Gewicht haben und damit sowohl exzitatorische als auch inhibitorische Synapsen nachahmen. Verändern sich die Verbindungsgewichte, spricht man von Lernen. Dies kann durch verschiedene Verfahren, sogenannte Lernregeln, realisiert werden. Die einfachste Lernregel, die sogenannte Hebb’sche Regel, besagt zum Beispiel, dass die Verbindung zwischen zwei Neuronen dann gestärkt wird, wenn diese gemeinsam aktiv sind. Dadurch werden assoziative Lernvorgänge erzielt. Knoten lassen sich zu Schichten zusammenfassen. In der Regel verfügen neuronale Netze über eine Input- und eine Outputschicht, in denen Aktivierungen entweder als Inputmuster erzeugt oder als Reaktion des Netzes abgelesen werden. Die meisten Modelle beinhalten dazwischen noch eine oder mehrere Schichten, sogenannte hidden layers, die einer komplexeren Verarbeitung dienen.
Funktionsweise eines Knotens
Knoten sind als simulierte Neurone kleine Recheneinheiten. Sie wandeln einen Input x in einen Output o um. Der Input ist ein Vektor aus Aktivierungsstärken oder Feuerraten. Dieser wird an den simulierten Synapsen gewichtet und schließlich aufsummiert, sodass ein einzelner Wert, der Netzinput, übrigbleibt. Um aus diesem die Outputaktivierung zu berechnen, wird eine Aktivierungsfunktion zwischengeschaltet, welche jedem Netzinput eine Outputstärke zuordnet. Dies kann zum Beispiel eine lineare Funktion, eine Sigmoidfunktion oder eine Schwellwertfunktion sein. Eine Schwellwertfunktion implementiert die Aktivierungsschwelle, die jedes einzelne natürliche Neuron auszeichnet. Bis zu einer bestimmten Inputstärke bleibt das Neuron inaktiv, bei darüber hinausgehendem Input entwickelt es ein Aktionspotential, es „feuert“. Dieser Schwellwert ist für jedes Neuron individuell und variiert über Neuone hinweg. An dieser Stelle ist es wichtig, das Knoten in Netzen oftmals nicht einzelne Neurone simulieren, sondern eigentlich viele Neurone, sogenannte Neuronenverbände (neural assemblies). Entsprechend unscharf wird die Aktivierungsschwelle des gesamten Knotens, denn einige Neurone feuern leichter und einige schwerer. Eine Sigmoidfunktion fasst diese individuellen Schwellwerte zusammen, indem sie die Aktivierungsstärke nicht mehr sprungartig, sondern soft, abhängig von der Anzahl der bereits feuernden Neurone, abbildet. Daher wird diese Aktivierungsfunktion oft für die Simulation biologischer Neuronenverbände verwendet.
kkk Ein einfaches neuronales Netz kann in der R-Shiny-App "Neuronale Netze" beobachtet und untersucht werden.