Kombinatorik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 10: | Zeile 10: | ||
==Permutation== | ==Permutation== | ||
*Eine Permutation ist eine geordnete Anordnung von Elementen | *Eine Permutation ist eine geordnete Anordnung von Elementen | ||
*Die Anzahl der Permutationen von ''n'' Elementen ist <math> n! </math> (''n'' Fakultät), wobei <math> n! = n\cdot(n-1)\cdot(n-2)\cdot...\ | *Die Anzahl der Permutationen von ''n'' Elementen ist <math> n! </math> (''n'' Fakultät), wobei <math> n! = n \cdot (n-1) \cdot (n-2) \cdot ... \cdot 3 \cdot 2 \cdot 1 </math> | ||
==Kombinationen== | ==Kombinationen== | ||
| Zeile 17: | Zeile 17: | ||
*Kombination ohne Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig | *Kombination ohne Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig | ||
*Kombination mit Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig, und Elemente können mehrfach ausgewählt werden | *Kombination mit Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig, und Elemente können mehrfach ausgewählt werden | ||
*Die Anzahl der Kombinationen ohne Wiederholung von ''n'' Elementen, die jeweils ''k'' Elemente enthalten, ist (''n'' über ''k''), berechnet als <math>{n | *Die Anzahl der Kombinationen ohne Wiederholung von ''n'' Elementen, die jeweils ''k'' Elemente enthalten, ist (''n'' über ''k''), berechnet als <math>{n\choosek} = \frac{n!}{k!\cdot(n-k)!}</math>. Man spricht bei dieser Größe vom '''Binomialkoeffizienten'''. | ||
==Variation== | ==Variation== | ||
| Zeile 28: | Zeile 28: | ||
==Multinomialkoeffizient== | ==Multinomialkoeffizient== | ||
Der Multinomialkoeffizient ist eine Verallgemeinerung des Binomialkoeffizienten (siehe Kombinationen) und gibt die Anzahl der Möglichkeiten an, ''n'' Objekte in ''k'' Gruppen aufzuteilen, wobei jede Gruppe eine bestimmte Größe hat. Er wird verwendet, wenn es mehr als zwei mögliche Kategorien oder Gruppen gibt, in die Objekte eingeteilt werden können. Wenn ''n'' Objekte in ''k'' Gruppen eingeteilt werden und die Gruppen die Größen <math>n_{1}, n_{2}, n_{3}, ..., n_{k},</math> haben, ist der Multinomialkoeffizient <math>{n}\choose{n_{1}, n_{2}, ..., n_{k}} = \frac{n!}{n_{1}! \cdot n_{2}! \cdot ... \cdot n_{k}!},</math> <br> | Der Multinomialkoeffizient ist eine Verallgemeinerung des Binomialkoeffizienten (siehe Kombinationen) und gibt die Anzahl der Möglichkeiten an, ''n'' Objekte in ''k'' Gruppen aufzuteilen, wobei jede Gruppe eine bestimmte Größe hat. Er wird verwendet, wenn es mehr als zwei mögliche Kategorien oder Gruppen gibt, in die Objekte eingeteilt werden können. Wenn ''n'' Objekte in ''k'' Gruppen eingeteilt werden und die Gruppen die Größen <math>n_{1}, n_{2}, n_{3}, ..., n_{k},</math> haben, ist der Multinomialkoeffizient <math>{{n}\choose{n_{1}, n_{2}, ..., n_{k}}} = \frac{n!}{n_{1}! \cdot n_{2}! \cdot ... \cdot n_{k}!},</math> <br> | ||
Wenn wir Beispielsweise 10 Objekte in drei Gruppen der Größen 3, 2 und 5 einteilen wollen, können wir die Anzahl der verschiedenen Möglichkeiten zur Einteilung wie folgt berechnen: <math>{10}\choose{2,3,5} = \frac{10!}{3! \cdot 2! \cdot 5!} = \frac{3628800}{6 \cdot 2 \cdot 120} = 2520</math> <br> | Wenn wir Beispielsweise 10 Objekte in drei Gruppen der Größen 3, 2 und 5 einteilen wollen, können wir die Anzahl der verschiedenen Möglichkeiten zur Einteilung wie folgt berechnen: <math>{{10}\choose{2,3,5}} = \frac{10!}{3! \cdot 2! \cdot 5!} = \frac{3628800}{6 \cdot 2 \cdot 120} = 2520</math> <br> | ||
Das bedeutet es gibt 2.520 verschiedene Möglichkeiten, 10 Objekte in drei Gruppen mit den Größen 3, 2 und 5 aufzuteilen. | Das bedeutet es gibt 2.520 verschiedene Möglichkeiten, 10 Objekte in drei Gruppen mit den Größen 3, 2 und 5 aufzuteilen. | ||
Version vom 28. August 2024, 10:36 Uhr
Grundbegriffe
- Grundmenge: In der Kombinatorik bezeichnet die "Grundmenge" oder "Ausgangsmenge" die Gesamtheit aller Elemente, aus denen man wählen kann. Die Grundmenge ist also die Menge, aus der man Kombinationen oder Permutationen bildet.
- Reihenfolge: Die Reihenfolge ist in der Kombinatorik die Abfolge, in der Elemente gezogen werden. Ob die Reihenfolge wichtig oder unwichtig ist, bedeutet, ob beachtet wird, welches Element zu welchem Zeitpunkt gezogen wird oder ob man nur die gesamte gezogene Menge ohne eine Ordnung betrachtet. Die Relevanz der Reihenfolge unterscheidet unter anderem Kombination und Variation (s.u.).
- Zurücklegen: (mit) Zurücklegen ist die Möglichkeit, ein Element nach seiner Auswahl zurückzulegen und erneut aus der gleichen Menge auszuwählen. Das Gegenteil davon wäre "ohne Zurücklegen", bei dem jedes Element nur einmal ausgewählt werden darf.
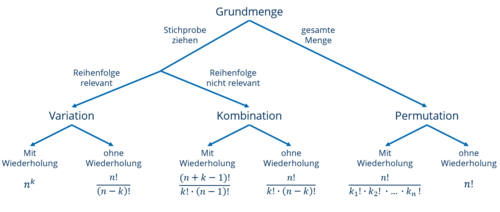
Ziehverfahren
Permutation
- Eine Permutation ist eine geordnete Anordnung von Elementen
- Die Anzahl der Permutationen von n Elementen ist (n Fakultät), wobei
Kombinationen
- Eine Kombination ist eine ungeordnete Auswahl von Elementen
- Es gibt zwei Haupttypen von Kombinationen:
- Kombination ohne Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig
- Kombination mit Wiederholung: Die Reihenfolge der Auswahl ist nicht wichtig, und Elemente können mehrfach ausgewählt werden
- Die Anzahl der Kombinationen ohne Wiederholung von n Elementen, die jeweils k Elemente enthalten, ist (n über k), berechnet als Fehler beim Parsen (Unbekannte Funktion „\choosek“): {\displaystyle {n\choosek} = \frac{n!}{k!\cdot(n-k)!}} . Man spricht bei dieser Größe vom Binomialkoeffizienten.
Variation
- Eine Variation ist eine geordnete Auswahl von Elementen
- Es gibt Variationen mit und ohne Wiederholung
- Die Anzahl der Variationen ohne Wiederholung von n Elementen, die jeweils k Elemente enthalten, ist
Multinomialkoeffizient
Der Multinomialkoeffizient ist eine Verallgemeinerung des Binomialkoeffizienten (siehe Kombinationen) und gibt die Anzahl der Möglichkeiten an, n Objekte in k Gruppen aufzuteilen, wobei jede Gruppe eine bestimmte Größe hat. Er wird verwendet, wenn es mehr als zwei mögliche Kategorien oder Gruppen gibt, in die Objekte eingeteilt werden können. Wenn n Objekte in k Gruppen eingeteilt werden und die Gruppen die Größen haben, ist der Multinomialkoeffizient
Wenn wir Beispielsweise 10 Objekte in drei Gruppen der Größen 3, 2 und 5 einteilen wollen, können wir die Anzahl der verschiedenen Möglichkeiten zur Einteilung wie folgt berechnen:
Das bedeutet es gibt 2.520 verschiedene Möglichkeiten, 10 Objekte in drei Gruppen mit den Größen 3, 2 und 5 aufzuteilen.