Trigonometrie: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 4: | Zeile 4: | ||
Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben: | Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben: | ||
*'''Sinus:''' das Verhältnis der Länge von Gegenkathete zur Hypothenuse <math>sin(\alpha) = \frac{a}{ | *'''Sinus:''' das Verhältnis der Länge von Gegenkathete zur Hypothenuse <math>sin(\alpha) = \frac{a}{b}</math> | ||
*'''Kosinus:''' das Verhältnis der Länge der Ankathete zur Hypotenuse <math>cos(\alpha) = \frac{ | *'''Kosinus:''' das Verhältnis der Länge der Ankathete zur Hypotenuse <math>cos(\alpha) = \frac{c}{b}</math> | ||
*'''Tangens:''' das Verhältnis der Länge der Gegenkathete zur Ankathete <math>tan(\alpha) = \frac{ | *'''Tangens:''' das Verhältnis der Länge der Gegenkathete zur Ankathete <math>tan(\alpha) = \frac{c}{a}</math> | ||
*'''Kotangens:''' das Reziprok des Tangens <math>cot(\alpha) = \frac{a}{ | *'''Kotangens:''' das Reziprok des Tangens <math>cot(\alpha) = \frac{a}{c}</math> | ||
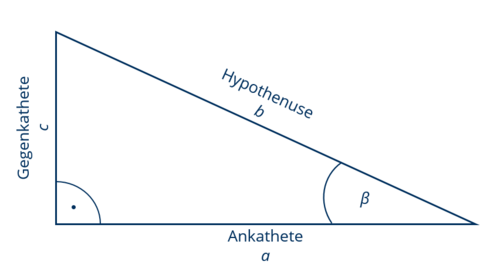
Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind. | Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind. | ||
[[Datei: | [[Datei:TrigDreieck.PNG|500px|zentriert]] | ||
Version vom 28. August 2024, 12:46 Uhr
Die Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen den Winkeln und Seitenlängen in Dreiecken beschäftigt.
Seitenverhältnisse
Die Verhältnisse der Seitenlängen in einem rechtwinkligen Dreieck in Bezug auf einen der nicht rechten Winkel lassen sich wie folgt beschreiben:
- Sinus: das Verhältnis der Länge von Gegenkathete zur Hypothenuse
- Kosinus: das Verhältnis der Länge der Ankathete zur Hypotenuse
- Tangens: das Verhältnis der Länge der Gegenkathete zur Ankathete
- Kotangens: das Reziprok des Tangens
Dabei ist die Hypothenuse die Seite, die dem rechten Winkel im Dreieck gegenüberliegt. Die Ankathete ist die Seite des Dreiecks, die neben der Hypthenuse am betreffenden Winkel anliegt. Die Gegenkathete liegt dem betreffenden Winkel gegenüber. Diese Funktionen erlauben es, Winkel in Dreiecken zu berechnen, wenn die Längen der Seiten bekannt sind, und umgekehrt die Seitenlängen zu bestimmen, wenn die Winkel bekannt sind.