Bootstrapping: Unterschied zwischen den Versionen

Version vom 6. März 2020, 00:04 Uhr

Die Bootstrap-Technik nach Efron (1979) ist ein Resampling-Verfahren, welches es ermög-licht, Parameter aus einer Stichprobe zu schätzen, ohne Annahmen über eine spezifische Verteilung zu treffen. Sie wird in der Praxis angewandt, wenn die untersuchten Werte keiner bekannten Verteilung folgen.

Das Prinzip des Bootstrapping beruht darauf, Informationen über eine unbekannte Po-pulation durch Resampling einer einzelnen Stichprobe aus dieser Population zu erhalten. Resampling bedeutet in diesem Fall, dass eine große Anzahl Bootstrap-Stichproben mit Zu-rücklegen aus der Ausgangsstichprobe gezogen werden. Dabei wird zunächst ein einzelner Wert gezogen und wieder in die Ausgangsstichprobe zurückgelegt. Dieser Vorgang wird so häufig wiederholt, bis die Bootstrap-Stichprobe die Größe der Ausgangsstichprobe erreicht hat. Durch das Zurücklegen kann eine Bootstrap-Stichprobe einzelne Werte der Ausgangs-stichprobe mehrfach, andere Werte wiederum gar nicht enthalten. Auf diese Art werden übli-cherweise mehrere tausend Bootstrap-Stichproben erzeugt. Für jede dieser Bootstrap-Stichproben kann z.B. der arithmetische Mittelwert x̅ oder ein anderer interessierender Para-meter geschätzt werden. Anhand der Verteilung der arithmetischen Mittelwerte der Bootstrap-Strichproben sind Rückschlüsse auf die Parameter der Population möglich. Eine häufige An-wendung ist die Berechnung valider Konfidenzintervalle für Parameter der Population. In Ab-bildung 1 sind die Mittelwerte und das 95%-Konfidenzintervall von 20000 Bootstrap-Stichproben dargestellt, die aus einer nicht-normalverteilten Ausgangsstichprobe mit einem Mittelwert von x̅ = 2.75 und einer Standardabweichung von s = 1.45 gezogen wurden. 95 % der Mittelwerte aller gezogenen Bootstrapstichproben befinden sich zwischen 2.36 und 3.15.

Als non-parametrisches Verfahren ohne Verteilungsannahmen ist Bootstrapping in vielen Kon-texten anwendbar, wie z.B. bei der Prüfung von indirekten Effekten bei linearen Strukturglei-chungsmodellen. Eine wichtige Voraussetzung für die Anwendung der Bootstrap-Technik ist jedoch, dass die Ausgangsstichprobe repräsentativ für die Grundgesamtheit sein muss. Au-ßerdem ist das Verfahren rechenintensiv, was besonders bei zunehmender Anzahl an Bootstrap-Stichproben berücksichtigt werden muss.

kkk Im Video wird die Bootstrap-Technik näher erläutert.

kkk Die Methode des Bootstrappings lässt sich in der interaktiven Simulation mit verschiedenen Ausgangsstichproben und für verschiedene Stichprobengrößen und Konfidenzniveaus nachvollziehen.

Weiterführende Literatur

Manly, B.F. (2018). Randomization, bootstrap and Monte Carlo Methods in biology. Chapman and Hall/CRC

Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 9.3). München: Pearson Studium.

@@ Zeile 1: / Zeile 1: @@
 {{Nav|Navigation|Statistik|Hauptseite}}
-Ein Konfidenzintervall oder Vertrauensintervall bezeichnet ein Intervall möglicher Parameterausprägungen, in dem sich ein untersuchter Populationsparameter mit der Wahrscheinlichkeit des Konfidenzniveaus (1-α) befindet. Das Konfidenzintervall gibt Informationen zur Genauigkeit der Punktschätzung eines untersuchten Populationsparameters, wie z.B. des arithmetischen Mittelwertes.
+Die Bootstrap-Technik nach Efron (1979) ist ein Resampling-Verfahren, welches es ermög-licht, Parameter aus einer Stichprobe zu schätzen, ohne Annahmen über eine spezifische Verteilung zu treffen. Sie wird in der Praxis angewandt, wenn die untersuchten Werte keiner bekannten Verteilung folgen.
-Die Größe des Konfidenzniveaus kann vom Anwender frei gewählt werden und hängt von der jeweiligen Fragestellung ab. Üblicherweise werden Konfidenzniveaus von 0.95 oder 0.99 gewählt. Ein Konfidenzniveau von 0.95 beschreibt z.B., dass 95 % der 95 %-Konfidenzintervalle der aus einer Grundgesamtheit gezogenen Stichproben den Erwartungswert μ der Grundgesamtheit überdecken, wenn aus derselben Grundgesamtheit sehr viele Stichproben gezogen werden. Dieser Sachverhalt wird in Abbildung 1 mit dem Erwartungswert μ = 100, einer Stichprobengröße n = 15 und der Standardabweichung in der Grundgesamtheit σ = 15 dargestellt.
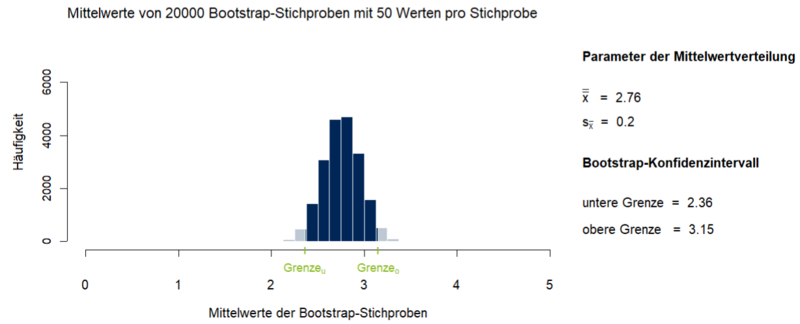
+Das Prinzip des Bootstrapping beruht darauf, Informationen über eine unbekannte Po-pulation durch Resampling einer einzelnen Stichprobe aus dieser Population zu erhalten. Resampling bedeutet in diesem Fall, dass eine große Anzahl Bootstrap-Stichproben mit Zu-rücklegen aus der Ausgangsstichprobe gezogen werden. Dabei wird zunächst ein einzelner Wert gezogen und wieder in die Ausgangsstichprobe zurückgelegt. Dieser Vorgang wird so häufig wiederholt, bis die Bootstrap-Stichprobe die Größe der Ausgangsstichprobe erreicht hat. Durch das Zurücklegen kann eine Bootstrap-Stichprobe einzelne Werte der Ausgangs-stichprobe mehrfach, andere Werte wiederum gar nicht enthalten. Auf diese Art werden übli-cherweise mehrere tausend Bootstrap-Stichproben erzeugt. Für jede dieser Bootstrap-Stichproben kann z.B. der arithmetische Mittelwert x̅ oder ein anderer interessierender Para-meter geschätzt werden. Anhand der Verteilung der arithmetischen Mittelwerte der Bootstrap-Strichproben sind Rückschlüsse auf die Parameter der Population möglich. Eine häufige An-wendung ist die Berechnung valider Konfidenzintervalle für Parameter der Population. In Ab-bildung 1 sind die Mittelwerte und das 95%-Konfidenzintervall von 20000 Bootstrap-Stichproben dargestellt, die aus einer nicht-normalverteilten Ausgangsstichprobe mit einem Mittelwert von x̅ = 2.75 und einer Standardabweichung von s = 1.45 gezogen wurden. 95 % der Mittelwerte aller gezogenen Bootstrapstichproben befinden sich zwischen 2.36 und 3.15.
-[[File:1_6_Konfidenzintervall.PNG|800px|Abbildung 1: Häufigkeitsverteilungen der Werte der Grundgesamtheit und der Grenzen des Konfidenzintervalls]]
+[[File:1_7_Bootstrapping.PNG|800px|Abbildung 1: Mittelwerte von 20000 Bootstrap-Stichproben (n=50) mit Darstellung des 95%-Konfidenzintervalls]]
-Die grüne und die dunkelblaue Markierung unterhalb der Verteilungen der Intervallgrenzen kennzeichnen diejenigen Fälle, in denen das Konfidenzintervall der Stichprobe den Erwartungswert der Grundgesamtheit nicht beinhaltet. In etwa 2.5 % der Fälle befindet sich die obere Grenze des Konfidenzintervalls unterhalb des Erwartungswertes (blau) und in 2.5 % der Fälle befindet sich die untere Grenze des Konfidenzintervalls oberhalb des Erwartungswertes μ = 100 (grün). Die untere Grenze G<sub>u</sub> und die obere Grenze G<sub>o<\sub> des Konfidenzintervalls lassen sich mithilfe der folgenden Formeln schätzen:
+Als non-parametrisches Verfahren ohne Verteilungsannahmen ist Bootstrapping in vielen Kon-texten anwendbar, wie z.B. bei der Prüfung von indirekten Effekten bei linearen Strukturglei-chungsmodellen. Eine wichtige Voraussetzung für die Anwendung der Bootstrap-Technik ist jedoch, dass die Ausgangsstichprobe repräsentativ für die Grundgesamtheit sein muss. Au-ßerdem ist das Verfahren rechenintensiv, was besonders bei zunehmender Anzahl an Bootstrap-Stichproben berücksichtigt werden muss.
-[[File:1_6_Konfidenzintervall_Formel.PNG|120px]]
-X̅ ist die Punktschätzung für den Populationsmittelwert, z<sub>1-α/2</sub> das Quantil der Standardnormalverteilung und σ<sub>X̅</sub> der Standardfehler der Punktschätzung des Populationsmittelwertes. Zur Berechnung des Standardfehlers wird die Standardabweichung der Population benötigt. Da diese häufig nicht bekannt ist, wird der Standardfehler des Stichprobenmittelwertes s<sub>X̅</sub> als Schätzwert für σ<sub>X̅</sub> verwendet (vgl. [[Standardfehler]]). Statt mit z-Werten der Standardnormalverteilung würden die Intervallgrenzen mit Quantilen der t-Verteilung bestimmt werden. Zum tieferen Verständnis sei auf Rudolf & Kuhlisch (2008) verwiesen.
-Die Breite des Konfidenzintervalls ist von verschiedenen Parametern abhängig. Ein höheres festgelegtes Konfidenzniveau (1-α), d.h. zum Beispiel 99% statt 95%, führt zu einem breiteren Konfidenzintervall. Je höher die Standardabweichung, desto breiter ist das Konfidenzintervall. Erhöht man den Stichprobenumfang, dann wird das Konfidenzintervall schmaler.
 [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/konfidenzintervall_link.html
-|120px]] <span style="color: white"> kkk </span>  Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird der die Entstehung eines Konfidenzintervalls näher erläutert.
+|120px]] <span style="color: white"> kkk </span>  Im [http://141.76.19.82:3838/mediawiki/pwertlink.html Video] wird die Bootstrap-Technik näher erläutert.
 [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/
-|120px]] <span style="color: white"> kkk </span>  Inwieweit das Konfidenzintervall von verschiedenen Parametern abhängig ist, lässt sich in der [http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ interaktiven Simulation] grafisch nachvollziehen.
+|120px]] <span style="color: white"> kkk </span>  Die Methode des Bootstrappings lässt sich in der [http://141.76.19.82:3838/mediawiki/1_1_p-Wert/App_Version/ interaktiven Simulation] mit verschiedenen Ausgangsstichproben und für verschiedene Stichprobengrößen und Konfidenzniveaus nachvollziehen.
 '''''Weiterführende Literatur'''''
+Manly, B.F. (2018). ''Randomization, bootstrap and Monte Carlo Methods in biology''. Chapman and Hall/CRC
 Rudolf, M., & Kuhlisch, W. (2008). ''Biostatistik: Eine Einführung für Biowissenschaftler'' (Kapitel 9.3). München: Pearson Studium.

Bootstrapping: Unterschied zwischen den Versionen

Version vom 6. März 2020, 00:04 Uhr

Navigationsmenü

Suche