Dynamische Attraktormodelle: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Mathematische Modelle|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Mathematische Modelle|Kognitive Modellierung|Hauptseite}} | ||
Differentialgleichungen werden häufig dafür verwendet, das Verhalten von dynamischen Systemen zu beschreiben. Unter dynamischen Systemen versteht man mathematische Modelle von zeitabhängigen Prozessen, in denen die weitere Entwicklung des Systems vom jeweiligen Anfangszustand abhängt. Mit ihnen kann man bspw. die Bewegung eines Pendels, Klima- oder Populationsveränderungen inklusive Räuber-Beute Interaktionen, aber auch kognitive Prozesse der Wahrnehmung und Entscheidung modellieren. | |||
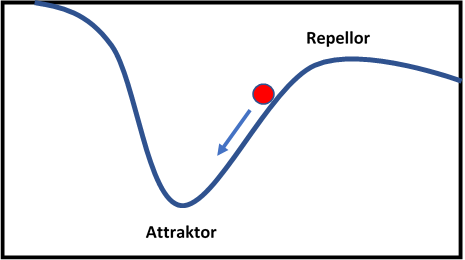
Eine spezielle Gruppe von dynamischen Modellen sind '''Attraktormodelle'''. Systeme mit einem Attraktor weisen eine gewisse Anzahl an Zuständen auf, an die sich ein dynamisches System im Laufe der Zeit annähert und dort schließlich verharrt. Nehmen wir an, ein dynamisches System hat genau eine Variable, die sich über die Zeit so verändert, wie es die entsprechende Differentialgleichung beschreibt. Diese Veränderung wird oft über eine sogenannte '''Potentiallandschaft''' oder Energielandschaft dargestellt. So sieht man in dem Beispieldiagramm unten das Veränderungspotential oder die Energie für jeden möglichen Zustand des Systems, also jeden möglichen Wert der Variable. Der aktuelle Zustand der Variable wird in dieser Potentiallandschaft als rote Kugel repräsentiert. Die Potentiallandschaft selbst gleicht einer Berg-Tal Landschaft und beschreibt, wie sich der aktuelle Zustand laut der Differentialgleichung ändern wird. Intuitiv gelesen bewegt sich der Ball von den Bergen in das nächstgelegene Tal. Wenn der Ball im Tal angekommen ist, spricht man von einem '''stabilen Systemzustand''' – er hat also kein Änderungspotential mehr, im Gegensatz zu den Bergen, bei welchen ein großes Potential zur Veränderung besteht. Stabile Systemzustände können auch komplexere Muster sein, als nur in einem Zustand zu verharren – also z.B. Zyklen von Zuständen. Da der Ball von den Tälern, also den stabilen Zuständen angezogen wird, nennt man diese Zustände auch '''Attraktoren'''. | |||
[[File:Attraktormodelle 01.png||600px]] | |||
Typische Attraktoren sind also: | |||
* '''Stabile Fixpunkte''': Das System nähert sich - wenn die Zeit gegen unendlich geht - immer stärker einem bestimmten Endzustand an, indem die Dynamik allmählich nachlässt. | |||
* '''Stabile Zyklen''': Hier ist der Endzustand kein einziger Zustand, sondern eine Abfolge immer gleicher Zustände, die sich periodisch abwechseln (Z.B. Räuber-Beute-Modell) | |||
Das Gegenteil von einem Attraktor – die Bergespitzen sozusagen - nennt man '''Repellor''', also einen Zustand, von dem sich das System wegbewegt. | |||
Version vom 25. September 2018, 17:07 Uhr
Differentialgleichungen werden häufig dafür verwendet, das Verhalten von dynamischen Systemen zu beschreiben. Unter dynamischen Systemen versteht man mathematische Modelle von zeitabhängigen Prozessen, in denen die weitere Entwicklung des Systems vom jeweiligen Anfangszustand abhängt. Mit ihnen kann man bspw. die Bewegung eines Pendels, Klima- oder Populationsveränderungen inklusive Räuber-Beute Interaktionen, aber auch kognitive Prozesse der Wahrnehmung und Entscheidung modellieren.
Eine spezielle Gruppe von dynamischen Modellen sind Attraktormodelle. Systeme mit einem Attraktor weisen eine gewisse Anzahl an Zuständen auf, an die sich ein dynamisches System im Laufe der Zeit annähert und dort schließlich verharrt. Nehmen wir an, ein dynamisches System hat genau eine Variable, die sich über die Zeit so verändert, wie es die entsprechende Differentialgleichung beschreibt. Diese Veränderung wird oft über eine sogenannte Potentiallandschaft oder Energielandschaft dargestellt. So sieht man in dem Beispieldiagramm unten das Veränderungspotential oder die Energie für jeden möglichen Zustand des Systems, also jeden möglichen Wert der Variable. Der aktuelle Zustand der Variable wird in dieser Potentiallandschaft als rote Kugel repräsentiert. Die Potentiallandschaft selbst gleicht einer Berg-Tal Landschaft und beschreibt, wie sich der aktuelle Zustand laut der Differentialgleichung ändern wird. Intuitiv gelesen bewegt sich der Ball von den Bergen in das nächstgelegene Tal. Wenn der Ball im Tal angekommen ist, spricht man von einem stabilen Systemzustand – er hat also kein Änderungspotential mehr, im Gegensatz zu den Bergen, bei welchen ein großes Potential zur Veränderung besteht. Stabile Systemzustände können auch komplexere Muster sein, als nur in einem Zustand zu verharren – also z.B. Zyklen von Zuständen. Da der Ball von den Tälern, also den stabilen Zuständen angezogen wird, nennt man diese Zustände auch Attraktoren.
Typische Attraktoren sind also:
- Stabile Fixpunkte: Das System nähert sich - wenn die Zeit gegen unendlich geht - immer stärker einem bestimmten Endzustand an, indem die Dynamik allmählich nachlässt.
- Stabile Zyklen: Hier ist der Endzustand kein einziger Zustand, sondern eine Abfolge immer gleicher Zustände, die sich periodisch abwechseln (Z.B. Räuber-Beute-Modell)
Das Gegenteil von einem Attraktor – die Bergespitzen sozusagen - nennt man Repellor, also einen Zustand, von dem sich das System wegbewegt.