Permutationstest: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
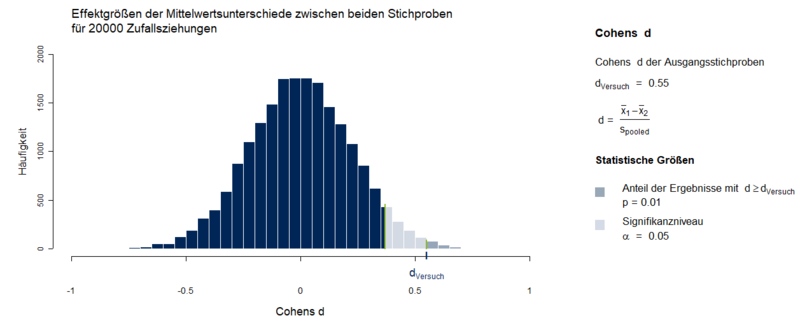
[[File:1_8_Permutationstest.PNG|800px|Abbildung 1: Permutationsverteilung aus 20000 Zufallsziehungen und Darstellung des p-Wertes für den gefundenen Mittelwertsunterschied der Stichproben]] | [[File:1_8_Permutationstest.PNG|800px|Abbildung 1: Permutationsverteilung aus 20000 Zufallsziehungen und Darstellung des p-Wertes für den gefundenen Mittelwertsunterschied der Stichproben|link=Ausgelagerte_Bildbeschreibungen#Permutationstest|Ausgelagerte Bildbeschreibung von Permutationstest]] | ||
Version vom 3. Februar 2022, 18:29 Uhr
Permutationstests bieten zum Beispiel die Möglichkeit, Mittelwertsvergleiche zweier unabhängiger Stichproben vorzunehmen, wenn die Voraussetzungen eines parametrischen Tests, wie des t-Tests, nicht erfüllt sind.
Für den Permutationstest wird in diesem Beispiel zunächst eine Nullhypothesen-Verteilung erzeugt, bei der angenommen wird, dass es keine Unterschiede zwischen beiden Grundgesamtheiten gibt. Die Daten der beiden Ausgangsstichproben werden wie eine Grundgesamtheit behandelt, aus welcher Permutationen erzeugt werden, d.h. es werden aus allen Daten Stichproben ohne Zurücklegen in der Größe der Ausgangsstichproben gezogen. Hätte man beispielsweise zwei Stichproben S1 und S2 mit den Werten S1: 3, 5, 2 und S2: 8, 4, 10, dann wären mögliche Permutationen dieser z.B. 3, 8, 2 und 10, 4, 5 oder 10, 5, 2 und 8, 3, 4. Es werden nun entweder alle Permutationskombinationen erschöpft (exakte Methode) oder bei größeren Stichproben eine große Anzahl an Permutationen durch Zufallsziehungen erzeugt (Annäherungsmethode). Für jede Kombination permutierter Stichproben wird der normierte Mittelwertsunterschied (Cohens d) berechnet. Aus diesen Mittelwertsunterschieden entsteht die Nullhypothesen-Verteilung, die auch als Permutationsverteilung bezeichnet wird. Um zu überprüfen, ob der Mittelwertsunterschied der Ausgangsstichproben signifikant von 0 verschieden ist, wird dieser auf der Verteilung verortet. Anschließend kann überprüft werden, wie wahrscheinlich es unter Gültigkeit der Nullhypothese ist, den Mittelwertsunterschied der Ausgangsstichproben oder einen der Nullhypothese noch stärker widersprechenden Mittelwertsunterschied zu erhalten (p-Wert). Dazu teilt man die Anzahl aller Werte gleich oder größer dem gefundenen Mittelwertsunterschied durch die Anzahl aller Werte der Permutationsverteilung. Der so berechnete p-Wert kann anschließend mit dem vorher festgelegten Signifikanzniveau α verglichen werden.
In Abbildung 1 werden die an der gepoolten Standardabweichung normierten Mittelwertsunterschiede (Cohens d) von 20000 Permutationen aus zwei unabhängigen Ausgangsstichproben der Größe n1 = n2 = 40 mit den Mittelwerten x̅1 = 1.32 und x̅2 = 0.87 bei einer gepoolten Standardabweichung von 1 dargestellt.
Eine wichtige Voraussetzung für die Anwendung des Permutationstest ist, dass die Ausgangsstichproben repräsentativ für die zugrundeliegenden Grundgesamtheiten sein müssen. Außerdem ist das Verfahren rechenintensiv und erfordert mit höherer Anzahl an Permutationen eine zunehmende Rechenleistung.
kkk Im Video wird der Permutationstest näher erläutert.
kkk In der interaktiven Simulation lassen sich Permutationstests für verschiedene Ausgangsstichproben und unterschiedliche Stichprobengrößen berechnen.
Weiterführende Literatur
Collingridge, D. S. (2013). A primer on quantitized data analysis and permutation testing. Journal of Mixed Methods Research, 7(1), 81-97.
Heiler, S., & Weichselberger, K. (1969). Über den Permutationstest und ein daraus ableitbares Konfidenzintervall. Metrika, 14(1), 232-248.