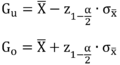Konfidenzintervalle: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Nadia1 (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation| | {{Nav|Navigation|Statistik_Grundbegriffe|Hauptseite}} | ||
Ein Konfidenzintervall oder Vertrauensintervall bezeichnet ein Intervall möglicher Parameterausprägungen, in dem sich ein untersuchter Populationsparameter mit der Wahrscheinlichkeit des Konfidenzniveaus (1-α) befindet. Das Konfidenzintervall gibt Informationen zur Genauigkeit der Punktschätzung eines untersuchten Populationsparameters, wie z.B. des arithmetischen Mittelwertes. | Ein Konfidenzintervall oder Vertrauensintervall bezeichnet ein Intervall möglicher Parameterausprägungen, in dem sich ein untersuchter Populationsparameter mit der Wahrscheinlichkeit des Konfidenzniveaus (1-α) befindet. Das Konfidenzintervall gibt Informationen zur Genauigkeit der Punktschätzung eines untersuchten Populationsparameters, wie z.B. des arithmetischen Mittelwertes. | ||
| Zeile 5: | Zeile 5: | ||
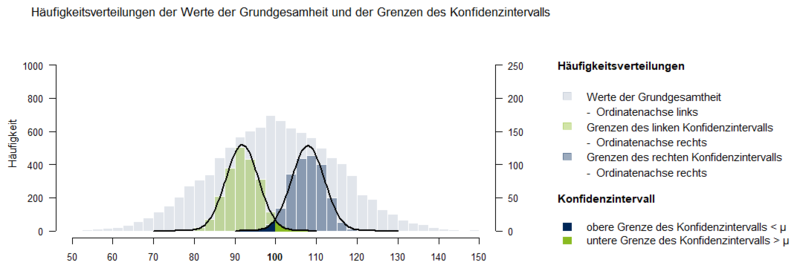
Die Größe des Konfidenzniveaus kann vom Anwender frei gewählt werden und hängt von der jeweiligen Fragestellung ab. Üblicherweise werden Konfidenzniveaus von 0.95 oder 0.99 gewählt. Ein Konfidenzniveau von 0.95 beschreibt z.B., dass 95 % der 95 %-Konfidenzintervalle der aus einer Grundgesamtheit gezogenen Stichproben den Erwartungswert μ der Grundgesamtheit überdecken, wenn aus derselben Grundgesamtheit sehr viele Stichproben gezogen werden. Dieser Sachverhalt wird in Abbildung 1 mit dem Erwartungswert μ = 100, einer Stichprobengröße n = 15 und der Standardabweichung in der Grundgesamtheit σ = 15 dargestellt. | Die Größe des Konfidenzniveaus kann vom Anwender frei gewählt werden und hängt von der jeweiligen Fragestellung ab. Üblicherweise werden Konfidenzniveaus von 0.95 oder 0.99 gewählt. Ein Konfidenzniveau von 0.95 beschreibt z.B., dass 95 % der 95 %-Konfidenzintervalle der aus einer Grundgesamtheit gezogenen Stichproben den Erwartungswert μ der Grundgesamtheit überdecken, wenn aus derselben Grundgesamtheit sehr viele Stichproben gezogen werden. Dieser Sachverhalt wird in Abbildung 1 mit dem Erwartungswert μ = 100, einer Stichprobengröße n = 15 und der Standardabweichung in der Grundgesamtheit σ = 15 dargestellt. | ||
Die grüne und die dunkelblaue Markierung unterhalb der Verteilungen der Intervallgrenzen kennzeichnen diejenigen Fälle, in denen das Konfidenzintervall der Stichprobe den Erwartungswert der Grundgesamtheit nicht beinhaltet. In etwa 2.5 % der Fälle befindet sich die obere Grenze des Konfidenzintervalls unterhalb des Erwartungswertes (blau) und in 2.5 % der Fälle befindet sich die untere Grenze des Konfidenzintervalls oberhalb des Erwartungswertes μ = 100 (grün). Die untere Grenze G<sub>u</sub> und die obere Grenze G<sub>o< | [[File:1_6_Konfidenzintervall.PNG|800px|Abbildung 1: Häufigkeitsverteilungen der Werte der Grundgesamtheit und der Grenzen des Konfidenzintervalls|link=Ausgelagerte_Bildbeschreibungen#Konfidenzintervalle|Ausgelagerte Bildbeschreibung von Konfidenzintervalle]] | ||
Die grüne und die dunkelblaue Markierung unterhalb der Verteilungen der Intervallgrenzen kennzeichnen diejenigen Fälle, in denen das Konfidenzintervall der Stichprobe den Erwartungswert der Grundgesamtheit nicht beinhaltet. In etwa 2.5 % der Fälle befindet sich die obere Grenze des Konfidenzintervalls unterhalb des Erwartungswertes (blau) und in 2.5 % der Fälle befindet sich die untere Grenze des Konfidenzintervalls oberhalb des Erwartungswertes μ = 100 (grün). Die untere Grenze G<sub>u</sub> und die obere Grenze G<sub>o</sub> des Konfidenzintervalls lassen sich mithilfe der folgenden Formeln schätzen: | |||
[[File:1_6_Konfidenzintervall_Formel.PNG|120px|link=Ausgelagerte_Formeln#Grenzen_eines_Konfidenzintervalls|Ausgelagerte Formeln obere und untere Grenzen eines Konfidenzintervalls]] | |||
X̅ ist die Punktschätzung für den Populationsmittelwert, z<sub>1-α/2</sub> das Quantil der Standardnormalverteilung und σ<sub>X̅</sub> der Standardfehler der Punktschätzung des Populationsmittelwertes. Zur Berechnung des Standardfehlers wird die Standardabweichung der Population benötigt. Da diese häufig nicht bekannt ist, wird der Standardfehler des Stichprobenmittelwertes s<sub>X̅</sub> als Schätzwert für σ<sub>X̅</sub> verwendet (vgl. [[Standardfehler]]). Statt mit z-Werten der Standardnormalverteilung würden die Intervallgrenzen mit Quantilen der t-Verteilung bestimmt werden. Zum tieferen Verständnis sei auf Rudolf & Kuhlisch (2008) verwiesen. | X̅ ist die Punktschätzung für den Populationsmittelwert, z<sub>1-α/2</sub> das Quantil der Standardnormalverteilung und σ<sub>X̅</sub> der Standardfehler der Punktschätzung des Populationsmittelwertes. Zur Berechnung des Standardfehlers wird die Standardabweichung der Population benötigt. Da diese häufig nicht bekannt ist, wird der Standardfehler des Stichprobenmittelwertes s<sub>X̅</sub> als Schätzwert für σ<sub>X̅</sub> verwendet (vgl. [[Standardfehler]]). Statt mit z-Werten der Standardnormalverteilung würden die Intervallgrenzen mit Quantilen der t-Verteilung bestimmt werden. Zum tieferen Verständnis sei auf Rudolf & Kuhlisch (2008) verwiesen. | ||
| Zeile 16: | Zeile 20: | ||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_6_Konfidenzintervalle_Link.html|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_6_Konfidenzintervalle_Link.html Video] wird der die Entstehung eines Konfidenzintervalls näher erläutert. | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/ | |||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_6_Konfidenzintervalle/ | |||
|120px]] <span style="color: white"> kkk </span> Inwieweit das Konfidenzintervall von verschiedenen Parametern abhängig ist, lässt sich in der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_6_Konfidenzintervalle/ interaktiven Simulation] grafisch nachvollziehen. | |||
'''''Weiterführende Literatur''''' | |||
Rudolf, M. & Kuhlisch, W. (2020). ''Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler'' (2. Aufl.). München: Pearson Studium. (Kapitel 4.2) | |||
Aktuelle Version vom 28. Februar 2023, 10:22 Uhr
Ein Konfidenzintervall oder Vertrauensintervall bezeichnet ein Intervall möglicher Parameterausprägungen, in dem sich ein untersuchter Populationsparameter mit der Wahrscheinlichkeit des Konfidenzniveaus (1-α) befindet. Das Konfidenzintervall gibt Informationen zur Genauigkeit der Punktschätzung eines untersuchten Populationsparameters, wie z.B. des arithmetischen Mittelwertes.
Die Größe des Konfidenzniveaus kann vom Anwender frei gewählt werden und hängt von der jeweiligen Fragestellung ab. Üblicherweise werden Konfidenzniveaus von 0.95 oder 0.99 gewählt. Ein Konfidenzniveau von 0.95 beschreibt z.B., dass 95 % der 95 %-Konfidenzintervalle der aus einer Grundgesamtheit gezogenen Stichproben den Erwartungswert μ der Grundgesamtheit überdecken, wenn aus derselben Grundgesamtheit sehr viele Stichproben gezogen werden. Dieser Sachverhalt wird in Abbildung 1 mit dem Erwartungswert μ = 100, einer Stichprobengröße n = 15 und der Standardabweichung in der Grundgesamtheit σ = 15 dargestellt.
Die grüne und die dunkelblaue Markierung unterhalb der Verteilungen der Intervallgrenzen kennzeichnen diejenigen Fälle, in denen das Konfidenzintervall der Stichprobe den Erwartungswert der Grundgesamtheit nicht beinhaltet. In etwa 2.5 % der Fälle befindet sich die obere Grenze des Konfidenzintervalls unterhalb des Erwartungswertes (blau) und in 2.5 % der Fälle befindet sich die untere Grenze des Konfidenzintervalls oberhalb des Erwartungswertes μ = 100 (grün). Die untere Grenze Gu und die obere Grenze Go des Konfidenzintervalls lassen sich mithilfe der folgenden Formeln schätzen:
X̅ ist die Punktschätzung für den Populationsmittelwert, z1-α/2 das Quantil der Standardnormalverteilung und σX̅ der Standardfehler der Punktschätzung des Populationsmittelwertes. Zur Berechnung des Standardfehlers wird die Standardabweichung der Population benötigt. Da diese häufig nicht bekannt ist, wird der Standardfehler des Stichprobenmittelwertes sX̅ als Schätzwert für σX̅ verwendet (vgl. Standardfehler). Statt mit z-Werten der Standardnormalverteilung würden die Intervallgrenzen mit Quantilen der t-Verteilung bestimmt werden. Zum tieferen Verständnis sei auf Rudolf & Kuhlisch (2008) verwiesen.
Die Breite des Konfidenzintervalls ist von verschiedenen Parametern abhängig. Ein höheres festgelegtes Konfidenzniveau (1-α), d.h. zum Beispiel 99% statt 95%, führt zu einem breiteren Konfidenzintervall. Je höher die Standardabweichung, desto breiter ist das Konfidenzintervall. Erhöht man den Stichprobenumfang, dann wird das Konfidenzintervall schmaler.
kkk Im Video wird der die Entstehung eines Konfidenzintervalls näher erläutert.
kkk Inwieweit das Konfidenzintervall von verschiedenen Parametern abhängig ist, lässt sich in der interaktiven Simulation grafisch nachvollziehen.
Weiterführende Literatur
Rudolf, M. & Kuhlisch, W. (2020). Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler (2. Aufl.). München: Pearson Studium. (Kapitel 4.2)