Indexbildung: Unterschied zwischen den Versionen
Diana (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
Für die Reduktion dieses Merkmalsraumes unterscheidet Lazarsfeld (1937) deskriptiv drei Wege: | Für die Reduktion dieses Merkmalsraumes unterscheidet Lazarsfeld (1937) deskriptiv drei Wege: | ||
===Funktionelle Reduktion=== | ===Funktionelle Reduktion=== | ||
[[File:Reduktion1.png|right|192px|text-top]] | [[File:Reduktion1.png|right|192px|text-top|link=Ausgelagerte_Bildbeschreibungen#Funktionelle_Reduktion|Ausgelagerte Bildbeschreibung von Funktionelle Reduktion ]] | ||
Oft treten bestimmte Kombinationen praktisch nicht auf. Bei Korrekter Durchführung eines Intelligenztests, der davon ausgeht, dass eine übergreifende Intelligenzeigenschaft gemessen wird, dürfte zum Beispiel ein Ergebnis wie stark unterdurchschnittliche Ergebnisse im figuralen und verbalen bei überdurchschnittlichen numerischen Fähigkeiten nicht auftreten und muss somit nicht einfließen.<br clear=all> | Oft treten bestimmte Kombinationen praktisch nicht auf. Bei Korrekter Durchführung eines Intelligenztests, der davon ausgeht, dass eine übergreifende Intelligenzeigenschaft gemessen wird, dürfte zum Beispiel ein Ergebnis wie stark unterdurchschnittliche Ergebnisse im figuralen und verbalen bei überdurchschnittlichen numerischen Fähigkeiten nicht auftreten und muss somit nicht einfließen.<br clear=all> | ||
===Beliebige Reduktion=== | ===Beliebige Reduktion=== | ||
[[File:Reduktion2.png|right|192px|text-top]] | [[File:Reduktion2.png|right|192px|text-top|link=Ausgelagerte_Bildbeschreibungen#Beliebige_Reduktion|Ausgelagerte Bildbeschreibung von Beliebige Reduktion ]] | ||
Für das Gesamtkonstrukt ist es oft sinnvoll, einzubeziehen, dass geringere Werte in einem Faktor durch hohe in einem anderen ausgeglichen werden können. Soll zum Beispiel sozialer Status durch die Merkmale Schulbildung und Einkommen dargestellt werden, so ist es nicht wichtig, ob ein durchschnittlicher Wert im sozialen Status durch mittlere Werte in beiden Merkmalen oder durch einen sehr hohen Wert bei Schulbildung und einen sehr niedrigen Wert bei Einkommen entstehen.<br clear=all> | Für das Gesamtkonstrukt ist es oft sinnvoll, einzubeziehen, dass geringere Werte in einem Faktor durch hohe in einem anderen ausgeglichen werden können. Soll zum Beispiel sozialer Status durch die Merkmale Schulbildung und Einkommen dargestellt werden, so ist es nicht wichtig, ob ein durchschnittlicher Wert im sozialen Status durch mittlere Werte in beiden Merkmalen oder durch einen sehr hohen Wert bei Schulbildung und einen sehr niedrigen Wert bei Einkommen entstehen.<br clear=all> | ||
===pragmatische Reduktion=== | ===pragmatische Reduktion=== | ||
[[File:Reduktion3.png|right|192px|text-top]] | [[File:Reduktion3.png|right|192px|text-top|link=Ausgelagerte_Bildbeschreibungen#Pragmatische_Reduktion|Ausgelagerte Bildbeschreibung von Pragmatische Reduktion]] | ||
In vielen Fällen ist es so, dass schon anhand der Theorie Kombinationen zusammengefasst werden können. Zum Beispiel, wenn die Theorie davon ausgeht, dass die Fächer Informatik und Mathematik auf quasi dieselben Fähigkeiten zurückgreifen.<br clear=all> | In vielen Fällen ist es so, dass schon anhand der Theorie Kombinationen zusammengefasst werden können. Zum Beispiel, wenn die Theorie davon ausgeht, dass die Fächer Informatik und Mathematik auf quasi dieselben Fähigkeiten zurückgreifen.<br clear=all> | ||
| Zeile 26: | Zeile 28: | ||
===Additive Indexbildung=== | ===Additive Indexbildung=== | ||
[[File:additiveindexbildung.png|right|256px|text-top]] | [[File:additiveindexbildung.png|right|256px|text-top|link=Ausgelagerte_Bildbeschreibungen#Additive_Indexbildung|Ausgelagerte Bildbeschreibung von Additive Indexbildung]] | ||
Wenn gleichwichtige Merkmale sich gegenseitig ergänzen und kompensieren, ist es sinnvoll, additiv vorzugehen. Im Beispiel zu “Schulischer Leistung im Mathematisch-Naturwissenschaftlichen Feld” können die Schulnoten in den ausgewählten Fächern einfach addiert werden, damit würde ein Index mit Werten zwischen 5 und 30 für das zu erhebende Merkmal stehen. Es ist davon auszugehen, dass die Werte einander kompensieren und ein Schüler mit | Wenn gleichwichtige Merkmale sich gegenseitig ergänzen und kompensieren, ist es sinnvoll, additiv vorzugehen. Im Beispiel zu “Schulischer Leistung im Mathematisch-Naturwissenschaftlichen Feld” können die Schulnoten in den ausgewählten Fächern einfach addiert werden, damit würde ein Index mit Werten zwischen 5 und 30 für das zu erhebende Merkmal stehen. Es ist davon auszugehen, dass die Werte einander kompensieren und ein Schüler mit | ||
: A = Ma + Phy + Che + Bio + Inf | : A = Ma + Phy + Che + Bio + Inf | ||
| Zeile 35: | Zeile 37: | ||
und die “Ausreißer”-Note an etwas anderem liegen könnte, hier im Fach Biologie zum Beispiel Leistungsverweigerung aus Ekel bei bestimmten praktischen Aufgaben. | und die “Ausreißer”-Note an etwas anderem liegen könnte, hier im Fach Biologie zum Beispiel Leistungsverweigerung aus Ekel bei bestimmten praktischen Aufgaben. | ||
Um den Index zu bilden, kann es oft, so auch in unserem Beispiel, sinnvoll sein, die Summe durch die Anzahl der Faktoren zu teilen, und so einen normierten/sinnvolleren Bereich (1-6 statt 5-30) zu erreichen. | Um den Index zu bilden, kann es oft, so auch in unserem Beispiel, sinnvoll sein, die Summe durch die Anzahl der Faktoren zu teilen, und so einen normierten/sinnvolleren Bereich (1-6 statt 5-30) zu erreichen. | ||
===Multiplikative Indexbildung=== | ===Multiplikative Indexbildung=== | ||
| Zeile 52: | Zeile 53: | ||
===gewichtete Additive Indexbildung=== | ===gewichtete Additive Indexbildung=== | ||
[[File:gewichteteadditiveindexbildung.png|right|256px|text-top]] | [[File:gewichteteadditiveindexbildung.png|right|256px|text-top|link=Ausgelagerte_Bildbeschreibungen#Gewichtete_Additive_Indexbildung|Ausgelagerte Bildbeschreibung von Gewichtete Additive Indexbildung]] | ||
Eine Erweiterung zur einfachen additiven Indexbildung ist die gewichtete. Dabei wird ebenfalls davon ausgegangen, dass Faktoren sich gegenseitig kompensieren können, allerdings unterschiedlich stark. So könnten zum Beispiel im Auswahlverfahren für ein Studium im Fach Biologie wieder die Fähigkeiten im Math.-Nat.-Bereich erhoben werden. Allerdings wäre es hier nicht sinnvoll, wenn eine schlechte Biologienote durch eine gute Informatiknote kompensiert werden könnte. Der Index könnte hier zum Beispiel so gebildet werden: | Eine Erweiterung zur einfachen additiven Indexbildung ist die gewichtete. Dabei wird ebenfalls davon ausgegangen, dass Faktoren sich gegenseitig kompensieren können, allerdings unterschiedlich stark. So könnten zum Beispiel im Auswahlverfahren für ein Studium im Fach Biologie wieder die Fähigkeiten im Math.-Nat.-Bereich erhoben werden. Allerdings wäre es hier nicht sinnvoll, wenn eine schlechte Biologienote durch eine gute Informatiknote kompensiert werden könnte. Der Index könnte hier zum Beispiel so gebildet werden: | ||
: C = 2*Ma + 2*Phy + 3*Che + 5*Bio + 1*Inf | : C = 2*Ma + 2*Phy + 3*Che + 5*Bio + 1*Inf | ||
Aktuelle Version vom 11. Februar 2022, 15:06 Uhr
Indexbildung
Ein Index ist ein Messwert für ein komplexes Merkmal. Dabei werden einzelne Indikatoren, die Teil des zu messenden Merkmals sind, als Faktoren des Konstruktes zu einer Variable zusammengefasst, die man als Index bezeichnet.
Sollen beispielsweise die Mathematisch-Naturwissenschaftlichen Fähigkeiten von Schülern anhand des schulischen Erfolges erhoben werden, so könnten Noten in Mathematik, Physik, Chemie, Biologie und Informatik aufgenommen werden und der Mittelwert als Index für das zu messende Merkmal “Schulische Leistung im Mathematisch-Naturwissenschaftlichen Bereich” dienen.
Der Index soll eine klare Größe sein, die auf einer Intervall- oder Ordinalskala gemessen werden kann.
Im Beispiel könnte es nun, bei 5 Fächern und 6 Noten, 30 verschiedene Kombinationen geben.
Die Qualität eines Indexes hängt letztlich davon ab, ob alle relevanten Faktoren enthalten und korrekt gewichtet sind.
Reduktion des Merkmalsraumes
Die Konstruktdimensionen (im Beispiel die verschiedenen Fächer mit ihrer jeweiligen Note) spannen den Merkmalsraum auf. Der Index stellt dann eine Reduktion dieses Merkmalsraumes dar (aus den fünf Dimensionen der fünf Fächer wird eine Dimension zur schulischen Leistung im Mathematisch-Naturwissenschaftlichen Bereich). Für die Reduktion dieses Merkmalsraumes unterscheidet Lazarsfeld (1937) deskriptiv drei Wege:
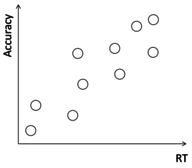
Funktionelle Reduktion
Oft treten bestimmte Kombinationen praktisch nicht auf. Bei Korrekter Durchführung eines Intelligenztests, der davon ausgeht, dass eine übergreifende Intelligenzeigenschaft gemessen wird, dürfte zum Beispiel ein Ergebnis wie stark unterdurchschnittliche Ergebnisse im figuralen und verbalen bei überdurchschnittlichen numerischen Fähigkeiten nicht auftreten und muss somit nicht einfließen.
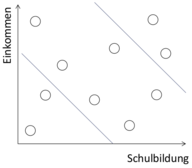
Beliebige Reduktion
Für das Gesamtkonstrukt ist es oft sinnvoll, einzubeziehen, dass geringere Werte in einem Faktor durch hohe in einem anderen ausgeglichen werden können. Soll zum Beispiel sozialer Status durch die Merkmale Schulbildung und Einkommen dargestellt werden, so ist es nicht wichtig, ob ein durchschnittlicher Wert im sozialen Status durch mittlere Werte in beiden Merkmalen oder durch einen sehr hohen Wert bei Schulbildung und einen sehr niedrigen Wert bei Einkommen entstehen.
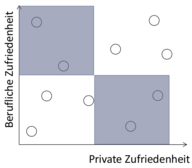
pragmatische Reduktion
In vielen Fällen ist es so, dass schon anhand der Theorie Kombinationen zusammengefasst werden können. Zum Beispiel, wenn die Theorie davon ausgeht, dass die Fächer Informatik und Mathematik auf quasi dieselben Fähigkeiten zurückgreifen.
Kombinieren der Merkmale
Nachdem festgelegt ist, welche Merkmale zusammengefasst werden sollen, muss entschieden werden, wie die Merkmale zu einem Index zusammengefasst werden.
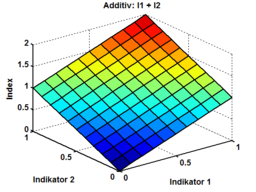
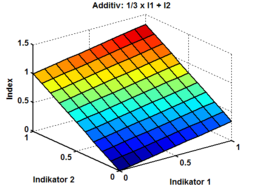
Additive Indexbildung
Wenn gleichwichtige Merkmale sich gegenseitig ergänzen und kompensieren, ist es sinnvoll, additiv vorzugehen. Im Beispiel zu “Schulischer Leistung im Mathematisch-Naturwissenschaftlichen Feld” können die Schulnoten in den ausgewählten Fächern einfach addiert werden, damit würde ein Index mit Werten zwischen 5 und 30 für das zu erhebende Merkmal stehen. Es ist davon auszugehen, dass die Werte einander kompensieren und ein Schüler mit
- A = Ma + Phy + Che + Bio + Inf
(A steht für den Index, hier: die allgemeine naturwissenschaftliche Fähigkeit)
- A1 = 1+1+1+6+1 = 10
tatsächlich bessere Fähigkeiten im Math.-Nat.-Bereich besitzt als einer mit
- A2 = 3+3+3+3+3 = 15
und die “Ausreißer”-Note an etwas anderem liegen könnte, hier im Fach Biologie zum Beispiel Leistungsverweigerung aus Ekel bei bestimmten praktischen Aufgaben. Um den Index zu bilden, kann es oft, so auch in unserem Beispiel, sinnvoll sein, die Summe durch die Anzahl der Faktoren zu teilen, und so einen normierten/sinnvolleren Bereich (1-6 statt 5-30) zu erreichen.
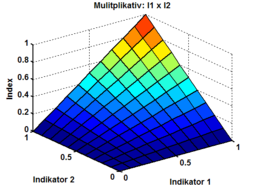
Multiplikative Indexbildung
Sollen sich die Merkmale nicht gegenseitig kompensieren, dann ist eine Multiplikation die beste
Wahl.
Zum Beispiel soll die Eignung von Bewerbern für eine Stelle als Programmierer ermittelt werden. Die Merkmale Programmierfähigkeit, Berufserfahrung und Gewissenhaftigkeit werden erhoben und von 0-3 Punkten bewertet. In diesem Fall würde es keinen Sinn ergeben, additiv vorzugehen, da ein gewissenhafter Bewerber mit großer Erfahrung, der allerdings kein bisschen programmieren kann (3+3+0 = 6) nicht genauso gut geeignet ist wie ein junger, eher gewissenhafter Bewerber mit wenig Erfahrung und exzellenten Fähigkeiten (2+1+3 = 6). Die Fähigkeiten sind alle unerlässlich und verstärken/schwächen einander, gleichen sich aber nicht aus.
In diesem Fall wäre es deshalb sinnvoll, multiplikativ vorzugehen. Der Index Berufseignung sähe nun so aus:
- B = Gew * Erf. * Prog.
- B1 = 3 * 3 * 0 = 0
- B2 = 2 * 1 * 3 = 6
Bei diesem Vorgehen fällt besonders stark ins Gewicht, wenn ein gesuchtes Merkmal komplett gar nicht vorhanden ist, hat eine Eigenschaft den Wert 0, so ist auch das Produkt stets 0
gewichtete Additive Indexbildung
Eine Erweiterung zur einfachen additiven Indexbildung ist die gewichtete. Dabei wird ebenfalls davon ausgegangen, dass Faktoren sich gegenseitig kompensieren können, allerdings unterschiedlich stark. So könnten zum Beispiel im Auswahlverfahren für ein Studium im Fach Biologie wieder die Fähigkeiten im Math.-Nat.-Bereich erhoben werden. Allerdings wäre es hier nicht sinnvoll, wenn eine schlechte Biologienote durch eine gute Informatiknote kompensiert werden könnte. Der Index könnte hier zum Beispiel so gebildet werden:
- C = 2*Ma + 2*Phy + 3*Che + 5*Bio + 1*Inf