Cronbach's Alpha: Unterschied zwischen den Versionen
Diana (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Cronbachs Alpha wird nach der folgenden Formel berechnet: | Cronbachs Alpha wird nach der folgenden Formel berechnet: | ||
[[Datei: | [[Datei:CA.png|600px|link=Ausgelagerte_Formeln#Cronbachs Alpha|Ausgelagerte Formel Cronbachs Alpha]] | ||
Der Koeffizient kann zwischen minus unendlich und plus 1 liegen. Hohe positive Werte entstehen dann, wenn die Items hoch positiv miteinander korrelieren. Negative Inter-Item-Korrelationen reduzieren den Wert von α und können im Extremfall negative Werte hervorbringen. Dann muss der Test überarbeitet oder es muss mit einer Faktorenanalyse nach Ursachen gesucht werden | Der Koeffizient kann zwischen minus unendlich und plus 1 liegen. Hohe positive Werte entstehen dann, wenn die Items hoch positiv miteinander korrelieren. Negative Inter-Item-Korrelationen reduzieren den Wert von α und können im Extremfall negative Werte hervorbringen. Dann muss der Test überarbeitet oder es muss mit einer Faktorenanalyse nach Ursachen gesucht werden | ||
Aktuelle Version vom 14. Februar 2022, 14:06 Uhr
Cronbachs Alpha (α) ist ein Koeffizient, welcher zur Bestimmung der internen Konsistenz eines Erhebungsverfahrens berechnet wird. Er gibt an, wie genau die Items eines Tests ein Konstrukt messen. Cronbachs Alpha ist der für die Berechnung der internen Konsistenz gebräuchlichste Koeffizient. Formal entspricht er der mittleren Testhalbierungs-Reliabilität eines Tests für alle möglichen Testhalbierungen (vgl. Bortz & Döring, 2006). Je mehr Items ein Test enthält, desto größer wird α. Der Koeffizient gibt also in Abhängigkeit von der Itemanzahl die Höhe der mittleren Itemzusammenhänge an. Zusätzlich gibt der Koeffizient die Homogenität eines Tests an, d. h. wie viele Items dasselbe messen. Es wird der Varianzanteil, der auf eine Merkmalsdimension zurückgeht, erfasst. Bei eindimensionalen Konstrukten fällt der Koeffizient deshalb höher aus als bei mehrdimensionalen Konstrukten.
Cronbachs Alpha wird nach der folgenden Formel berechnet:
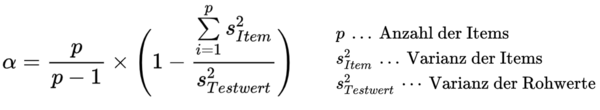
Der Koeffizient kann zwischen minus unendlich und plus 1 liegen. Hohe positive Werte entstehen dann, wenn die Items hoch positiv miteinander korrelieren. Negative Inter-Item-Korrelationen reduzieren den Wert von α und können im Extremfall negative Werte hervorbringen. Dann muss der Test überarbeitet oder es muss mit einer Faktorenanalyse nach Ursachen gesucht werden