Reinforcement Learning: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
[[File:RL Schema.png|| | [[File:RL Schema.png||500px|link=Ausgelagerte_Bildbeschreibungen#Markov-Entscheidungsproblem|Ausgelagerte Bildbeschreibung von Markov-Entscheidungsproblem]] | ||
| Zeile 21: | Zeile 21: | ||
== RL-Algorithmen == | == RL-Algorithmen == | ||
'''Temporal Difference (TD) Learning''' eignet sich dafür, die optimale Wertfunktion eines bestimmten Zustands zu bestimmen: | '''Temporal Difference (TD) Learning''' eignet sich dafür, die optimale Wertfunktion eines bestimmten Zustands zu bestimmen: | ||
Basierend auf einer Sequenz von Zuständen ''s'' zu den Zeitschritten ''t'' (bis ''T''), denen jeweils bestimmte Belohnungen ''r'' folgen: | Basierend auf einer Sequenz von Zuständen ''s'' zu den Zeitschritten ''t'' (bis ''T'' ), denen jeweils bestimmte Belohnungen ''r'' folgen: | ||
''s<sub>t</sub>, r<sub>t+1</sub>, s<sub>t+1</sub>, r<sub>t+2</sub>, …, r<sub>T</sub>, s<sub>T</sub>'' | ''s<sub>t</sub>, r<sub>t+1</sub>, s<sub>t+1</sub>, r<sub>t+2</sub>, …, r<sub>T</sub>, s<sub>T</sub>'' | ||
| Zeile 31: | Zeile 32: | ||
berechnet man die Wertfunktion ''V(s)'' des Zustands ''s'': | berechnet man die Wertfunktion ''V(s)'' des Zustands ''s'': | ||
''V(s)'' = ''E<sub>π</sub>'' (''R<sub>t</sub>'' | ''s<sub>t</sub>'') | ''V(s)'' = ''E<sub>π</sub>'' (''R<sub>t</sub>'' | ''s<sub>t</sub>'') | ||
''π''(''a'' | ''s'') = ''P''(''a<sub>t</sub> = a'' | ''s<sub>t</sub> = s'') | |||
''π''(''a'' | ''s'') = ''P'' (''a<sub>t</sub> = a'' | ''s<sub>t</sub> = s'') | |||
Wobei ''π'' die eingesetzte Strategie und ''E'' den Erwartungswert für den in Zukunft erwarteten Gesamtertrag ''R<sub>t</sub>'', der von dem Zustand ''s<sub>t</sub>'' ausgeht, darstellen. | Wobei ''π'' die eingesetzte Strategie und ''E'' den Erwartungswert für den in Zukunft erwarteten Gesamtertrag ''R<sub>t</sub>'', der von dem Zustand ''s<sub>t</sub>'' ausgeht, darstellen. | ||
| Zeile 55: | Zeile 57: | ||
Über diese Approximation kann zusätzlich zur Wertfunktion der Zustände die optimale Strategie oder Policy für den Zustandsraum ermittelt werden. | Über diese Approximation kann zusätzlich zur Wertfunktion der Zustände die optimale Strategie oder Policy für den Zustandsraum ermittelt werden. | ||
== Probleme und Einschränkungen == | == Probleme und Einschränkungen == | ||
| Zeile 81: | Zeile 81: | ||
[[File:RL | [[File:RL Schema2.png||600px|link=Ausgelagerte_Bildbeschreibungen#Reinforcement-Learning|Ausgelagerte Bildbeschreibung von Reinforcement-Learning]] | ||
Aktuelle Version vom 3. Januar 2022, 19:05 Uhr
„Of several responses made to the same situation, those which are accompanied or closely followed by satisfaction to the animal will…be more likely to recur.“
Dieses von Thorndike bereits im Jahre 1911 postulierte Effekt-Gesetz („Law of Effect“) und die darauf aufbauenden Prinzipien der instrumentellen Konditionierung besitzen noch heute beträchtliche Erklärungskraft und sind aktuell in Form von sog. Reinforcement Learning Models (Modelle verstärkenden Lernens) in der kognitiven und komputationalen Modellierung zu finden. Beim Reinforcement Learning (RL) geht es darum, dass ein Agent (z.B. eine simulierte Versuchsperson) nicht über konkrete Hinweise oder Richtigstellungen lernt, sondern über die Konsequenzen seiner Handlungen. Konsequenzen, sog. Verstärkersignale, sind numerische Belohnungen (oder Bestrafungen), welche den Erfolg eines Handlungsausgangs repräsentieren. Der Agent versucht dabei kontinuierlich zu lernen, welche Handlungen er auswählen muss, um die gesammelte Belohnung über die Zeit zu maximieren.
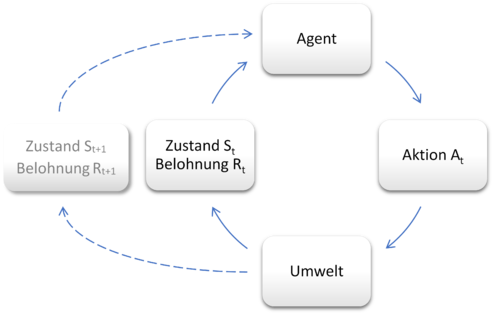
Die Interaktion des lernenden Agenten mit seiner Umwelt wird dabei als sog. Markov-Entscheidungsproblem (Markov Decision Problem, MDP) beschrieben:
Der Agent kann eine endliche Anzahl an Zuständen einnehmen. Durch Aktionen in seiner Umwelt kann er von einem Zustand in nachfolgende Zustände gelangen und dort eine numerische Belohnung erhalten. Anhand der Belohnungen, die der Agent durch seine Handlungen – also die Wahl von verschiedenen Zuständen ausgehend von dem momentanen Zustand – erhält, bemisst sich für jeden Zustand der Belohnungswert. Die Auswahl von Aktionen erfolgt anhand von sogenannten Strategien (Policies). Diese Strategien werden zur Maximierung der erwarteten akkumulierten Belohnung (dem Gesamtertrag) kontinuierlich verbessert.
RL versucht eine optimale Strategie zu finden, welche die Gesamtbelohnung über die Zustände hinweg maximiert. Dazu wird eine Wertfunktion für die jeweilige Strategie erlernt. Diese Funktion beschreibt für jeden eingenommenen Zustand dessen Wert, also wie viel zukünftige Belohnung man erwarten kann, wenn man von diesem Zustand ausgehend verschiedene Aktionen durchführt. Dabei gibt es verschiedene Methoden und Algorithmen, die optimale Wertfunktion und Strategie zu bestimmen z.B. „Temporal Difference Learning“ oder „Q-Learning“.
RL-Algorithmen
Temporal Difference (TD) Learning eignet sich dafür, die optimale Wertfunktion eines bestimmten Zustands zu bestimmen:
Basierend auf einer Sequenz von Zuständen s zu den Zeitschritten t (bis T ), denen jeweils bestimmte Belohnungen r folgen:
st, rt+1, st+1, rt+2, …, rT, sT
berechnet man die Wertfunktion V(s) des Zustands s:
V(s) = Eπ (Rt | st)
π(a | s) = P (at = a | st = s)
Wobei π die eingesetzte Strategie und E den Erwartungswert für den in Zukunft erwarteten Gesamtertrag Rt, der von dem Zustand st ausgeht, darstellen.
Soll die zunehmende Abwertung zeitlich entfernterer Belohnungen berücksichtigt werden, kann dies durch eine sogenannte Discountrate γ (< 1) repräsentiert werden: Rt = rt+1 + γ1 rt+2 + … + γT-t-1 rT
RL nimmt an, dass der Wert eines Zustands V(s) äquivalent zu dem erwarteten Gesamtertrag Rt ist. Die Aktualisierung der Wertfunktion - das Lernen - erfolgt also durch den Abgleich von V(s) mit Rt :
V(st)neu = V(st)alt + α [ Rt – V(st)alt ]
Die Schrittgröße (oder Lernrate) wird dabei durch α (oft α = 1) repräsentiert. Wenn V(st) den erwarteten Gesamtertrag Rt korrekt vorhersagt, wird die Aktualisierung der Wertfunktion im Mittel Null betragen und der finale Wert gefunden sein.
Im Q-Learning wird ergänzend zu den Belohnungs- und Zustandsparametern der Handlungsparameter a eingeführt, der beim TD Learning nicht spezifiziert war:
Q(s, a) = Eπ (Rt | st , at)
Über ein ähnliches Vorgehen wie beim TD Learning wird Q approximiert:
Q(st, at)neu = Q(st, at)alt + α [ rt+1 + γ Q(st+1, at+1) – Q(st, at) ]
Über diese Approximation kann zusätzlich zur Wertfunktion der Zustände die optimale Strategie oder Policy für den Zustandsraum ermittelt werden.
Probleme und Einschränkungen
Der RL Ansatz hat trotz seines großen Nutzens für viele Fragestellungen mit mehreren Problemen zu kämpfen, von denen einige hier vorgestellt werden:
- Dimensionalität: Bei der vergleichsweise realistischen Nachstellung realer RL Probleme kann es zu einer großen Anzahl von möglichen Zuständen und Handlungen kommen, die in einer explosionsartigen Menge von Zustands-Handlungs-Kombinationen resultieren.
- Mit Funktionsapproximationen bzw. Interpolationen des Werteraums sowie einer Generalisierung der Wertefunktion wird dieses Problem zu lösen versucht.
- Verspätete Belohnungen: In manchen Zustands-Handlungs-Räumen trifft die Belohnung erst sehr spät ein, d.h., es werden viele Aktionen durchgeführt und Zustände eingenommen, bis die Belohnung erscheint. Dies kann dazu führen, dass nur die Zustände, die der Belohnung zeitlich nahe vorausgehen, in ihrer Wertfunktion beeinflusst werden. Es braucht deshalb viele Schritte bis sich eine verspätete Belohnung auf alle Zustände und Aktionen auswirkt.
- Das Problem wird auf ähnliche Weise wie das Dimensionalitätsproblem gelöst.
- Unvollständige Beobachtbarkeit: In realen Situationen weiß ein Agent oft nicht, in welchem Zustand er sich nach einer bestimmten Handlung exakt befinden wird. Einfache RL-Algorithmen setzen jedoch volle Beobachtbarkeit voraus.
- Dieses Problem wird durch „Partial observable Markov Decision Problems“ (POMDP) Methoden gelöst.
- Nicht-stationäre Umwelten: RL-Algorithmen brauchen etwas Zeit für den Optimierungsprozess. Wenn die Umwelt sich dabei zu schnell verändert, ist das Lernen quasi unmöglich und die Annäherungsmethode schlägt fehl.
Anwendungen des Reinforcement Learning
RL-Algorithmen wie TD Learning werden u.a. als Modelle für dopaminerges Lernen in den Basalganglien verwendet. So kodieren bestimmte dopaminerge Projektionen aus dem Mittelhirn einen Belohnungsvorhersagefehler. Auch das Erlernen von Fähig- und Fertigkeiten bei Menschen wird häufig mit Hilfe von RL modelliert, besonders im Kontext von implizitem Lernen.
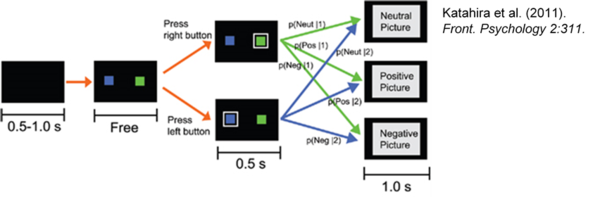
So lässt sich mit Hilfe von RL-Modellen auch der Effekt der emotionalen Valenz von Bildern (also ob sie als positiv, neutral oder negativ wahrgenommen werden) auf nachfolgende Entscheidungen überprüfen, wie es Katahira und Kollegen (2011) untersucht haben. In ihrer Studie wurden die Versuchspersonen instruiert, in 600 Durchgängen per Knopfdruck einen von zwei Zielreizen (blaues oder grünes Quadrat in der Abbildung unten) zu wählen. Die Entscheidung führte dann je nach ausgewähltem Zielreiz mit einer gewissen Wahrscheinlichkeit (grüne und blaue Pfeile) zu Bild-Outcomes unterschiedlicher Valenz (Neutral, Positiv, Negativ), also p(Valenz|Entscheidung). Zum Beispiel war der grüne Reiz häufiger mit positiven Bildern und der blaue häufiger mit negativen Bildern assoziiert. Diese bedingten Wahrscheinlichkeiten wurden dann aber über die Blöcke hinweg immer wieder verändert. Nach dem Experiment wurde jedes Bild separat auf seine Valenz von den Versuchspersonen eingeschätzt.
Aus Sicht eine Reinforcement Modells stellen in dieser künstlichen Umwelt (dem Experiment) die Bilder die Zustände da, in die der Agent (Versuchsperson) mittels Wahl der blauen oder grünen Quadrate wechseln kann. Die Valenz der Bilder spiegelt den Belohnungs-Outcome wider.
Indem man nun das Verhalten eines solchen Modells an das Verhalten jeder Versuchperson fitted, kann man untersuchen wie bestimmte Parameter das Entscheidungsverhalten beeinflussen, wie es sich über die Zeit verändert, je nachdem welche Entscheidung zu welchen Bildern führen. Finden die anfangs naiven Versuchspersonen eine Regel heraus bzw. bleiben sie bei positiven Erfahrungen mit einem Zielreiz konsistent bei dieser Entscheidung? Spiegelt das Entscheidungsverhalten die Valenz der Bilder wieder? Tatsächlich konnte man über das Entscheidungsverhalten mittels des RL-Modells einen Wert für die Bilder bestimmen, der den späteren Valenz-Ratings sehr ähnlich war. (Positive) emotionale Bilder stellen also auch für sich belohnende Reize dar.