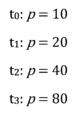Differentialgleichungsmodelle: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (15 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
Nehmen wir als einfaches Beispiel das exponentielle Wachstum einer Bakterienkolonie der Größe p=10 zum Startzeitpunkt t<sub>0</sub>. In einer (sehr künstlichen) hypothetischen Umwelt verdoppeln sich die Bakterien ohne zu sterben zu jedem Zeitschritt t: | Nehmen wir als einfaches Beispiel das exponentielle Wachstum einer Bakterienkolonie der Größe p=10 zum Startzeitpunkt t<sub>0</sub>. In einer (sehr künstlichen) hypothetischen Umwelt verdoppeln sich die Bakterien ohne zu sterben zu jedem Zeitschritt t: | ||
[[File:Differential F1.png|center|80px]] | [[File:Differential F1.png|center|80px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 1|Ausgelagerte Formel Differentialgleichungsmodelle 1]] | ||
Mathematisch könnte man die Entwicklung der Population in einer exponentiellen Formel zusammenfassen: | Mathematisch könnte man die Entwicklung der Population in einer exponentiellen Formel zusammenfassen: | ||
[[File:Differential F2.png|center|600px]] | [[File:Differential F2.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 2|Ausgelagerte Formel Differentialgleichungsmodelle 2]] | ||
Wir können aber auch das Wachstum von Zeitpunkt zu Zeitpunkt beschreiben, wie wir es beobachtet haben. Dann könnten wir schreiben | Wir können aber auch das Wachstum von Zeitpunkt zu Zeitpunkt beschreiben, wie wir es beobachtet haben. Dann könnten wir schreiben: | ||
[[File:Differential F3.png|center|600px]] | [[File:Differential F3.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 3|Ausgelagerte Formel Differentialgleichungsmodelle 3]] | ||
Von Zeitschritt zu Zeitschritt verdoppelt sich also die Population jeweils. Es könnte sein, dass eine andere Kolonie aber stärker oder schwächer wächst. Um das Modell zu verallgemeinern, können wir die Wachstumsrate, also die bisherige Verdoppelung, mit der Variablen α bezeichnen: | |||
[[File:Differential F4.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 4|Ausgelagerte Formel Differentialgleichungsmodelle 4]] | |||
Bisher haben wir die Zeit in ganzzahligen Schritten „portioniert“. Wenn wir nun die Zeit in kleinere Schritte als 1 aufteilen, dann bezeichnen wir diese Schritte als ∆t. Machen wir diese Schritte immer kleiner, dann betrachten wir die Zeit als kontinuierlich. Mit dieser Veränderung ist der Bakterienzuwachs (über den Faktor α) in einem Zeitintervall ∆t proportional zur Länge dieses Zeitintervalls und der Größe der Population: | |||
[[File:Differential F5.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 5|Ausgelagerte Formel Differentialgleichungsmodelle 5]] | |||
Diese Formel können wir umstellen, um auf der rechten Seite nur noch die Veränderung zu haben: | |||
[[File:Differential F6.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 6|Ausgelagerte Formel Differentialgleichungsmodelle 6]] | |||
Auf der rechten Seite steht jetzt also nur noch, wie sich das System zu einem bestimmten Zeitpunkt verändert, während auf der linken Seite dieser Gleichung der Differenzquotient steht. Für kontinuierliche Zeit, also unendlich kleine Zeitschritte, betrachten wir den Grenzwert für ∆t gegen 0. Das ist nichts anderes als die erste Ableitung, also die Änderung der Population über die (kontinuierliche) Zeit. So erhalten wir die Differentialgleichung | |||
[[File:Differential F7.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 7|Ausgelagerte Formel Differentialgleichungsmodelle 7]] | |||
und damit | |||
[[File:Differential F8.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 8|Ausgelagerte Formel Differentialgleichungsmodelle 8]] | |||
Differentialgleichungen kann man auch ausdrücken als eine Differenz ''d'' pro Zeiteinheit, in unserem Falle also die Differenz ''dp'' pro Zeiteinheit ''dt'': | |||
[[File:Differential F9.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 9|Ausgelagerte Formel Differentialgleichungsmodelle 9]] | |||
Dieser Ausdruck dient dazu, unendlich kleine Unterschiede in den Werten von p und t zu repräsentieren (=> das sogenannte Differential). Um unsere Differentialgleichung zu lösen, müssen wir eine Funktion ''„p(t) = …“'' finden, deren Ableitung unsere Differentialgleichung ergibt. | |||
Ein sehr bekanntes Beispiel für Differentialgleichungsmodelle aus dem Bereich der Psychologie, das Differentialgleichungen nutzt, ist das mit dem Nobelpreis gekrönte [https://de.wikipedia.org/wiki/Hodgkin-Huxley-Modell Hodgkin-Huxley-Modell], welches die Entstehung von Aktionspotentialen in Neuronen beschreibt. | |||
Wie kann man diese Differentialgleichungen nun in der Modellierung nutzen? In der Regel geschieht dies durch Simulation der Gleichungen an einem Computer. | |||
== Simulation == | |||
Während manche Differentialgleichungen in einfacher Form ausgerechnet (man sagt: gelöst) werden können, ist für viele dieser Gleichungen keine explizite Lösung möglich. Man nähert sich daher der Lösung mittels numerischer Verfahren an – das bedeutet, man simuliert die Gleichung Zeitschritt für Zeitschritt an einem Computer, so wie wir es oben für t = [1,2,3] gezeigt haben. Die Differentialgleichung sagt uns, wie sich eine Größe über die kontinuierliche Zeit verändert, weshalb es möglich ist, die Veränderung der Größe zu simulieren, wenn man sie in mehr oder weniger großen Zeitschritten aktualisiert. Man geht folgendermaßen vor: Man multipliziert die Veränderung des Werts der interessierenden Größe mit der abgelaufenen Zeit und addiert dies zum alten Wert um einen neuen Wert zu bekommen. Der neue Wert wird zum alten Wert und erfährt ebenso eine Veränderung. Je nachdem wie groß die Zeitschritte sind, kann es dabei allerdings zu einer fehlerhaften Annäherung kommen. | |||
Um psychologische Prozesse in ihrer Komplexität und ihren vielen Interaktionen zu modellieren, ist das oben aufgeführte Beispiel des Bakterienwachstums natürlich viel zu einfach. Betrachten wir daher – noch etwas in der Biologie bleibend - ein komplexeres Populationsmodell mit mehreren Ausgangsvariablen, das [https://de.wikipedia.org/wiki/Lotka-Volterra-Regeln Räuber-Beute-Modell von Lotka und Volterra (1925)], welches das obige Bakterienmodell auf den Fall von zwei Arten erweitert (z.B. Hasen und Füchse). Durch ihre Räuber-Beute Beziehung (Fuchs frisst Hase) weißen beide Populationen eine dynamische Kopplung zueinander auf (je mehr Füchse, desto mehr Verluste für die Hasen – je mehr Hasen, desto mehr Erfolg für die Füchse), aber auch jeweils eine Rückkopplung (Hasen haben eine Geburtenrate, Füchse eine Sterberate). In einer vereinfachten Form des Modells kann man also die Veränderung beider Populationen durch folgende Differentialgleichungen beschreiben: | |||
[[File:Differential F10.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 10|Ausgelagerte Formel Differentialgleichungsmodelle 10]] | |||
[[File:Differential F11.png|center|600px|link=Ausgelagerte Formeln#Differentialgleichungsmodelle 11|Ausgelagerte Formel Differentialgleichungsmodelle 11]] | |||
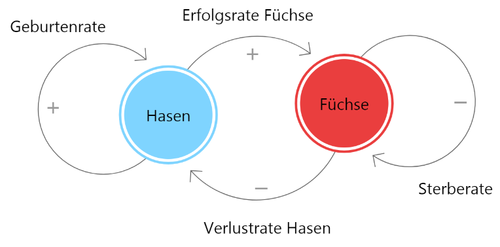
Die sehr zu empfehlende [ncase.me Webseite] des Grafikers Nicky Case bietet die Möglichkeit unterschiedliche Modelle nachzubauen, umzuformen und zu simulieren. Unter dem folgenden [https://bit.ly/2R01jyT Link] kann das oben beschriebene Räuber-Beute-Modell ausprobiert und verändert werden (z.B. durch Veränderung der Stärke der Knoten oder Menge der Pfeile). Das Modell sähe grafisch so aus: | |||
[[File:Differential HaseFuchs1.png|center|500px|link=Ausgelagerte_Bildbeschreibungen#Hase_Fuchs_Simulation_1|Ausgelagerte Bildbeschreibung von Hase Fuchs Simulation 1]] | |||
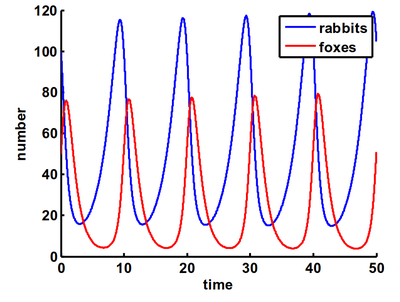
Simuliert man die Räuber-Beute-Dynamik über die Zeit, erhält man – sofern beide Populationen in einem ökologischen Gleichgewicht stehen (z.B. nicht zu viele Füchse oder Hasen am Anfang existieren) - folgenden Verlauf: | |||
[[File:Differential HaseFuchs2.png|center|400px|link=Ausgelagerte_Bildbeschreibungen#Hase_Fuchs_Simulation_2|Ausgelagerte Bildbeschreibung von Hase Fuchs Simulation 2]] | |||
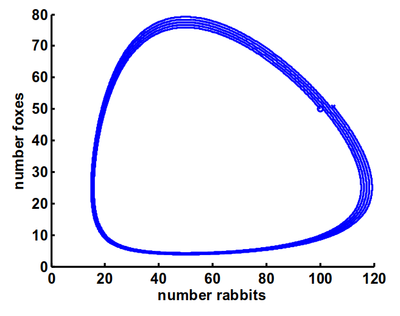
Bei dieser Räuber-Beute Beziehung spricht man auch von einem '''dynamischen System''': man hat mehrere Größen, hier die Population der Hasen und Füchse, die sich gegenseitig beeinflussen (und somit ein System bilden) und so über die Zeit verändern (also dynamisch). Die Veränderungsmusster eines solchen Systems kann man auch in seinem sogenannten Zustandsraum betrachten – also eine Abbildung der Kombination der verschiedenen möglichen Werte, welche die beiden Populationen gleichzeitig annehmen können. Muster, die sich in dieser Darstellung als stabil herausstellen, nennt man Attraktoren oder Gleichgewichtszustände, da das System sozusagen von ihnen angezogen wird und sich in diesen Mustern stabil einfindet. | |||
[[File:Differential HaseFuchs3.png|center|400px|link=Ausgelagerte_Bildbeschreibungen#Dynamisches_System|Ausgelagerte Bildbeschreibung von Dynamisches System]] | |||
In diesem Fall ist dieser Gleichgewichtszustand ein zyklisches Wechseln zwischen einer Mehrheit an Hasen oder Füchsen. Wodurch sich solche dynamischen Systeme charakterisieren und was ein Attraktor ist, erklärt der folgende [[Dynamische Attraktormodelle|Artikel]] mit Beispielen aus der kognitionspsychologischen Forschung ausführlicher. | |||
Aktuelle Version vom 17. Januar 2022, 14:54 Uhr
Viele Prozesse, die modelliert werden sollen, durchlaufen eine zeitliche Entwicklung: Wenn man wie in einem Film sehr viele Einzelbilder des Prozesses nacheinander machen würde, dann könnte man sehen, wie sich der Prozess langsam Schritt für Schritt entwickelt bzw. verändert. Man könnte beim Ansehen der Bilder zu der Annahme kommen, dass jeder Schritt auf den vorherigen Schritten aufbaut, so wie wir beim Denken den Eindruck haben, dass ein Gedanke den nächsten ergibt.
Das mathematische Werkzeug um solche zeitlichen Entwicklungen von Systemen und Prozessen darzustellen sind Differentialgleichungen. Differentialgleichungen sind mathematische Gleichungen, die eine Veränderung (eine Differenz) abbilden. Mathematisch gesprochen: Sie setzen eine bestimmte Funktion mit ihrer Ableitung in Beziehung. Konkret heißt das, dass die Differentialgleichung den Zusammenhang zwischen einer bestimmten Größe zum Zeitpunkt t, und der daraus folgenden Veränderung dieser Größe beschreibt. Den aktuellen Wert bezeichnet man entsprechend mit f(t), und die Veränderung, besser gesagt die Veränderungsrate dieser Größe mit f‘(t).
Zum einfacheren Verständnis führen wir im Folgenden Differentialgleichungen anhand von Modellen aus unserer Nachbardisziplin, der Biologie, ein. Diese Modelle sind aufgrund ihres Gegenstandes etwas leichter greifbar als die psychologischen Versionen.
Nehmen wir als einfaches Beispiel das exponentielle Wachstum einer Bakterienkolonie der Größe p=10 zum Startzeitpunkt t0. In einer (sehr künstlichen) hypothetischen Umwelt verdoppeln sich die Bakterien ohne zu sterben zu jedem Zeitschritt t:
Mathematisch könnte man die Entwicklung der Population in einer exponentiellen Formel zusammenfassen:
Wir können aber auch das Wachstum von Zeitpunkt zu Zeitpunkt beschreiben, wie wir es beobachtet haben. Dann könnten wir schreiben:
Von Zeitschritt zu Zeitschritt verdoppelt sich also die Population jeweils. Es könnte sein, dass eine andere Kolonie aber stärker oder schwächer wächst. Um das Modell zu verallgemeinern, können wir die Wachstumsrate, also die bisherige Verdoppelung, mit der Variablen α bezeichnen:
Bisher haben wir die Zeit in ganzzahligen Schritten „portioniert“. Wenn wir nun die Zeit in kleinere Schritte als 1 aufteilen, dann bezeichnen wir diese Schritte als ∆t. Machen wir diese Schritte immer kleiner, dann betrachten wir die Zeit als kontinuierlich. Mit dieser Veränderung ist der Bakterienzuwachs (über den Faktor α) in einem Zeitintervall ∆t proportional zur Länge dieses Zeitintervalls und der Größe der Population:
Diese Formel können wir umstellen, um auf der rechten Seite nur noch die Veränderung zu haben:
Auf der rechten Seite steht jetzt also nur noch, wie sich das System zu einem bestimmten Zeitpunkt verändert, während auf der linken Seite dieser Gleichung der Differenzquotient steht. Für kontinuierliche Zeit, also unendlich kleine Zeitschritte, betrachten wir den Grenzwert für ∆t gegen 0. Das ist nichts anderes als die erste Ableitung, also die Änderung der Population über die (kontinuierliche) Zeit. So erhalten wir die Differentialgleichung
und damit
Differentialgleichungen kann man auch ausdrücken als eine Differenz d pro Zeiteinheit, in unserem Falle also die Differenz dp pro Zeiteinheit dt:
Dieser Ausdruck dient dazu, unendlich kleine Unterschiede in den Werten von p und t zu repräsentieren (=> das sogenannte Differential). Um unsere Differentialgleichung zu lösen, müssen wir eine Funktion „p(t) = …“ finden, deren Ableitung unsere Differentialgleichung ergibt.
Ein sehr bekanntes Beispiel für Differentialgleichungsmodelle aus dem Bereich der Psychologie, das Differentialgleichungen nutzt, ist das mit dem Nobelpreis gekrönte Hodgkin-Huxley-Modell, welches die Entstehung von Aktionspotentialen in Neuronen beschreibt.
Wie kann man diese Differentialgleichungen nun in der Modellierung nutzen? In der Regel geschieht dies durch Simulation der Gleichungen an einem Computer.
Simulation
Während manche Differentialgleichungen in einfacher Form ausgerechnet (man sagt: gelöst) werden können, ist für viele dieser Gleichungen keine explizite Lösung möglich. Man nähert sich daher der Lösung mittels numerischer Verfahren an – das bedeutet, man simuliert die Gleichung Zeitschritt für Zeitschritt an einem Computer, so wie wir es oben für t = [1,2,3] gezeigt haben. Die Differentialgleichung sagt uns, wie sich eine Größe über die kontinuierliche Zeit verändert, weshalb es möglich ist, die Veränderung der Größe zu simulieren, wenn man sie in mehr oder weniger großen Zeitschritten aktualisiert. Man geht folgendermaßen vor: Man multipliziert die Veränderung des Werts der interessierenden Größe mit der abgelaufenen Zeit und addiert dies zum alten Wert um einen neuen Wert zu bekommen. Der neue Wert wird zum alten Wert und erfährt ebenso eine Veränderung. Je nachdem wie groß die Zeitschritte sind, kann es dabei allerdings zu einer fehlerhaften Annäherung kommen.
Um psychologische Prozesse in ihrer Komplexität und ihren vielen Interaktionen zu modellieren, ist das oben aufgeführte Beispiel des Bakterienwachstums natürlich viel zu einfach. Betrachten wir daher – noch etwas in der Biologie bleibend - ein komplexeres Populationsmodell mit mehreren Ausgangsvariablen, das Räuber-Beute-Modell von Lotka und Volterra (1925), welches das obige Bakterienmodell auf den Fall von zwei Arten erweitert (z.B. Hasen und Füchse). Durch ihre Räuber-Beute Beziehung (Fuchs frisst Hase) weißen beide Populationen eine dynamische Kopplung zueinander auf (je mehr Füchse, desto mehr Verluste für die Hasen – je mehr Hasen, desto mehr Erfolg für die Füchse), aber auch jeweils eine Rückkopplung (Hasen haben eine Geburtenrate, Füchse eine Sterberate). In einer vereinfachten Form des Modells kann man also die Veränderung beider Populationen durch folgende Differentialgleichungen beschreiben:
Die sehr zu empfehlende [ncase.me Webseite] des Grafikers Nicky Case bietet die Möglichkeit unterschiedliche Modelle nachzubauen, umzuformen und zu simulieren. Unter dem folgenden Link kann das oben beschriebene Räuber-Beute-Modell ausprobiert und verändert werden (z.B. durch Veränderung der Stärke der Knoten oder Menge der Pfeile). Das Modell sähe grafisch so aus:
Simuliert man die Räuber-Beute-Dynamik über die Zeit, erhält man – sofern beide Populationen in einem ökologischen Gleichgewicht stehen (z.B. nicht zu viele Füchse oder Hasen am Anfang existieren) - folgenden Verlauf:
Bei dieser Räuber-Beute Beziehung spricht man auch von einem dynamischen System: man hat mehrere Größen, hier die Population der Hasen und Füchse, die sich gegenseitig beeinflussen (und somit ein System bilden) und so über die Zeit verändern (also dynamisch). Die Veränderungsmusster eines solchen Systems kann man auch in seinem sogenannten Zustandsraum betrachten – also eine Abbildung der Kombination der verschiedenen möglichen Werte, welche die beiden Populationen gleichzeitig annehmen können. Muster, die sich in dieser Darstellung als stabil herausstellen, nennt man Attraktoren oder Gleichgewichtszustände, da das System sozusagen von ihnen angezogen wird und sich in diesen Mustern stabil einfindet.
In diesem Fall ist dieser Gleichgewichtszustand ein zyklisches Wechseln zwischen einer Mehrheit an Hasen oder Füchsen. Wodurch sich solche dynamischen Systeme charakterisieren und was ein Attraktor ist, erklärt der folgende Artikel mit Beispielen aus der kognitionspsychologischen Forschung ausführlicher.