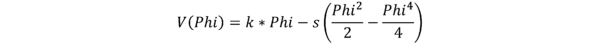Dynamische Attraktormodelle: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) |
||
| (11 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[File:Attraktormodelle 01.png|center|400px]] | [[File:Attraktormodelle 01.png|center|400px|link=Ausgelagerte_Bildbeschreibungen#Dynamische_Attraktormodelle|Ausgelagerte Bildbeschreibung von Dynamische Attraktormodelle]] | ||
| Zeile 22: | Zeile 22: | ||
Ein Beispiel für ein Attraktormodell aus der Psychologie ist das Wahrnehmungsmodell von Tuller und Kollegen. Sie stellten 1994 ein Modell zur Beschreibung der dynamischen Kategorisierung von gesprochenen Wörtern auf um zum Beispiel erklären zu können, unter welchen Umständen man das Wort „say“ oder „stay“ hört. Dabei verwendeten Sie eine spannende Manipulation: wenn man bei dem Wort „say“ zwischen s und a eine Lücke einbaut, dann hört man unter Umständen das Wort „stay“. Je größer die Lücke, desto stärker wir die Wahrnehmung von „stay“, je kleiner, desto eher hört man „say“. Es gibt also Länge der Lücke, bei der die beiden Wahrnehmungen gleich stark sind. Hier setzt das Modell an. Beide Wahrnehmungen sind in dem Modell potentiell stabile Zustände mit jeweils eigenem Attraktor, wie es in der Potentiallandschaft dargestellt ist. | Ein Beispiel für ein Attraktormodell aus der Psychologie ist das Wahrnehmungsmodell von Tuller und Kollegen. Sie stellten 1994 ein Modell zur Beschreibung der dynamischen Kategorisierung von gesprochenen Wörtern auf um zum Beispiel erklären zu können, unter welchen Umständen man das Wort „say“ oder „stay“ hört. Dabei verwendeten Sie eine spannende Manipulation: wenn man bei dem Wort „say“ zwischen s und a eine Lücke einbaut, dann hört man unter Umständen das Wort „stay“. Je größer die Lücke, desto stärker wir die Wahrnehmung von „stay“, je kleiner, desto eher hört man „say“. Es gibt also Länge der Lücke, bei der die beiden Wahrnehmungen gleich stark sind. Hier setzt das Modell an. Beide Wahrnehmungen sind in dem Modell potentiell stabile Zustände mit jeweils eigenem Attraktor, wie es in der Potentiallandschaft dargestellt ist. | ||
[[File:Attraktormodelle 02.png|center|600px]] | [[File:Attraktormodelle 02.png|center|600px|link=Ausgelagerte_Bildbeschreibungen#Modell_von_Tuller|Ausgelagerte Bildbeschreibung von Modell von Tuller]] | ||
Die Variable '''Phi''' repräsentiert dabei alle möglichen Zustände, die das System einnehmen kann: also unterschiedliche Grade der eindeutigen Interpretation als „say“ (Phi = -1) oder als „stay“ (Phi = 1). Der Startzustand, also der Zustand in dem Moment, wo man den Stimulus hört, ist neutral (Phi = 0, hier als momentaner Zustand wo die rote Kugel liegt). Das Modell beschreibt nun die Dynamik des Kategorisierungsprozesses über die folgende Gleichung (aus der die gezeigte Potentiallandschaft hergeleitet wird): | Die Variable '''Phi''' repräsentiert dabei alle möglichen Zustände, die das System einnehmen kann: also unterschiedliche Grade der eindeutigen Interpretation als „say“ (Phi = -1) oder als „stay“ (Phi = 1). Der Startzustand, also der Zustand in dem Moment, wo man den Stimulus hört, ist neutral (Phi = 0, hier als momentaner Zustand wo die rote Kugel liegt). Das Modell beschreibt nun die Dynamik des Kategorisierungsprozesses über die folgende Gleichung (aus der die gezeigte Potentiallandschaft hergeleitet wird): | ||
[[File:Attraktormodelle 03.png|center|600px]] | [[File:Attraktormodelle 03.png|center|600px|link=Ausgelagerte_Formeln#Modell von Tuller 1|Ausgelagerte Formel Modell von Tuller 1]] | ||
Um die Veränderung des Systemzustands über die Zeit berechnen zu können benötigen wir die Ableitung dieser Funktion: | Um die Veränderung des Systemzustands über die Zeit berechnen zu können benötigen wir die Ableitung dieser Funktion: | ||
[[File:Attraktormodelle 04.png|center|600px]] | [[File:Attraktormodelle 04.png|center|600px|link=Ausgelagerte_Formeln#Modell von Tuller 2|Ausgelagerte Formel Modell von Tuller 2]] | ||
Die Veränderung von Phi über die Zeit können wir dann durch folgende Differentialgleichung beschreiben: | Die Veränderung von Phi über die Zeit können wir dann durch folgende Differentialgleichung beschreiben: | ||
[[File:Attraktormodelle 05.png|center|600px]] | [[File:Attraktormodelle 05.png|center|600px|link=Ausgelagerte_Formeln#Modell von Tuller 3|Ausgelagerte Formel Modell von Tuller 3]] | ||
| Zeile 43: | Zeile 43: | ||
Dieses Modell kann nun nicht nur zur Modellierung der Kategorisierung von „say“ und „stay“ verwendet werden, sondern auch auf alle anderen mehrdeutigen Stimuli angewandt werden, z.B. die '''Wahrnehmung des Neckerwürfels''': | Dieses Modell kann nun nicht nur zur Modellierung der Kategorisierung von „say“ und „stay“ verwendet werden, sondern auch auf alle anderen mehrdeutigen Stimuli angewandt werden, z.B. die '''Wahrnehmung des Neckerwürfels''': | ||
[[File:Attraktormodelle 06.png|center|400px]] | [[File:Attraktormodelle 06.png|center|400px|link=Ausgelagerte_Bildbeschreibungen#Wahrnehmung_des_Neckerwürfels|Ausgelagerte Bildbeschreibung von Wahrnehmung des Neckerwürfels]] | ||
| Zeile 49: | Zeile 49: | ||
Für ein besseres Verständnis der beiden Parameter steht die Webapp | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MathematischeModelle/|120px]] <span style="color: white"> kkk </span>Für ein besseres Verständnis der beiden Parameter steht die Webapp [http://141.76.19.82:3838/mediawiki/MathematischeModelle/ Dynamische Attraktormodelle] zur Verfügung. | ||
Dort ist es möglich den dynamischen Prozess einer perzeptuellen Entscheidung („Welche Seite des Neckerwürfels sehe ich vorne?“) über eine Animation zu beobachten und durch Manipulation diverser Parameter zu beeinflussen, zum Beispiel wie sehr Rauschen den Prozess beeinflusst und wie einfach eine Wahrnehmung durch eine Störung des Prozesses (Perturbation) beeinflusst werden kann. | |||
== Eigenschaften dynamischer Modelle == | == Eigenschaften dynamischer Modelle == | ||
Am Beispiel des Modells von Tuller et al. können wir viele typische Eigenschaften dynamischer Modelle erkennen: | Am Beispiel des Modells von Tuller et al. können wir viele typische Eigenschaften dynamischer Modelle erkennen: | ||
'''Multistabilität''': Es existieren mehrere Attraktoren mit unterschiedlichen Attraktorbecken gleichzeitig, d.h., mehrere Endzustände sind je nach Ausgangszustand möglich. | '''Multistabilität''': Es existieren mehrere Attraktoren mit unterschiedlichen Attraktorbecken gleichzeitig, d.h., mehrere Endzustände sind je nach Ausgangszustand möglich. | ||
| Zeile 65: | Zeile 66: | ||
Wenn wir z.B. k (den Input) schrittweise erhöhen, im Experiment mit dem Necker-Würfel also die rechten vorderen Kanten des Würfels weniger sichtbar machen, dann verschiebt sich das Gewicht der beiden Attraktoren so, dass der linke Attraktor (Wahrnehmung: „Neckerwürfel von unten“) im Vergleich zum rechten (Wahrnehmung: „Neckerwürfel von oben“) immer stärker wird. Bei einer bestimmten Ausprägung von k (der relativen Sichtbarkeit der verschiedenen Würfelkanten) führt nun jede noch so minimale weitere Änderung des Parameters (also z.B. eine weitere minimale Ausblendung der Würfelkanten) dazu, dass es nur noch ein statt zwei Attraktorbecken gibt (es könnte nur noch eine Richtung des Würfels gesehen werden). Dieser Übergang von einem (multistabilen) System mit 2 Attraktoren zu einem monostabilen System mit nur einem Attraktor bezeichnet man als Bifurkation – ebenso wie die Gegenrichtung, wenn aus einem monostabilen System ein bistabiles System wird. | Wenn wir z.B. k (den Input) schrittweise erhöhen, im Experiment mit dem Necker-Würfel also die rechten vorderen Kanten des Würfels weniger sichtbar machen, dann verschiebt sich das Gewicht der beiden Attraktoren so, dass der linke Attraktor (Wahrnehmung: „Neckerwürfel von unten“) im Vergleich zum rechten (Wahrnehmung: „Neckerwürfel von oben“) immer stärker wird. Bei einer bestimmten Ausprägung von k (der relativen Sichtbarkeit der verschiedenen Würfelkanten) führt nun jede noch so minimale weitere Änderung des Parameters (also z.B. eine weitere minimale Ausblendung der Würfelkanten) dazu, dass es nur noch ein statt zwei Attraktorbecken gibt (es könnte nur noch eine Richtung des Würfels gesehen werden). Dieser Übergang von einem (multistabilen) System mit 2 Attraktoren zu einem monostabilen System mit nur einem Attraktor bezeichnet man als Bifurkation – ebenso wie die Gegenrichtung, wenn aus einem monostabilen System ein bistabiles System wird. | ||
[[File:Attraktormodelle 07.png|center|600px]] | [[File:Attraktormodelle 07.png|center|600px|link=Ausgelagerte_Bildbeschreibungen#Eigenschaften_Attraktormodell|Ausgelagerte Bildbeschreibung von Eigenschaften Attraktormodell]] | ||
Das spannende an der Bifurkation ist, dass hier die Nichtlinearität des Systems zum Tragen kommt. Im Vergleich zu den vorherigen Parameterveränderungen, können wir also mit der gleichen Schrittweite das System jetzt in seiner Qualität (ein statt zwei Attraktoren) deutlich verändern. Die Auswirkungen dieser Nichtlinearität und der dadurch entstehenden Bifurkationen spiegelt sich als Verhalten in der sogenannten Hysterese wider. | Das spannende an der Bifurkation ist, dass hier die Nichtlinearität des Systems zum Tragen kommt. Im Vergleich zu den vorherigen Parameterveränderungen, können wir also mit der gleichen Schrittweite das System jetzt in seiner Qualität (ein statt zwei Attraktoren) deutlich verändern. Die Auswirkungen dieser Nichtlinearität und der dadurch entstehenden Bifurkationen spiegelt sich als Verhalten in der sogenannten Hysterese wider. | ||
| Zeile 74: | Zeile 75: | ||
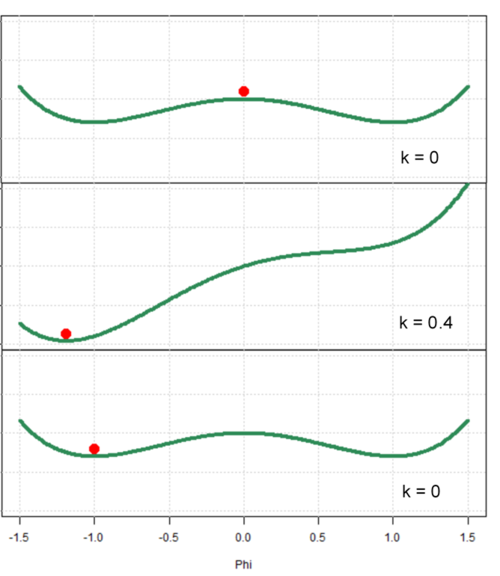
In unserem Beispiel könnten wir im Experiment den Neckerwürfel zunächst mit gleich starken Kanten präsentieren (im Modell k = 0, siehe Abbildung), sodass keine Interpretation sich durchsetzt (der Systemzustand Phi also in der Mitte verharrt). Anschließend könnten wir die oberen rechten Kanten abschwächen (k = 0.4), sodass die „Neckerwürfel von unten“-Interpretation die Überhand gewinnt (d.h. Phi zum linken Attraktor strebt). In einem linearen System würde nun ein Rückgängigmachen dieser Parameteränderung (zurück zu k = 0 bzw. gleich starke Würfelkanten) auch zu einer Rückkehr des Systemzustands zum Anfangszustand führen (also Phi = 0). Da bei nichtlinearen Systemen aber die Vorgeschichte eine zentrale Rolle spielt, kann diese Änderung nicht einfach wieder durch k rückgängig gemacht werden, wie man im untersten Teil der Abbildung sieht. Stattdessen bewegt sich Phi nur minimal zum leicht verschobenen linken Attraktor und die Interpretation „Neckerwürfel von unten“ bleibt trotz mehrdeutiger Präsentation (k = 0) erhalten. Wir können in diesem System also für k = 0 zwei (und in Abhängigkeit des Zeitverlaufs viele weitere) Systemzustände beobachten, auch wenn alle anderen Parameter des Modells konstant gehalten werden. | In unserem Beispiel könnten wir im Experiment den Neckerwürfel zunächst mit gleich starken Kanten präsentieren (im Modell k = 0, siehe Abbildung), sodass keine Interpretation sich durchsetzt (der Systemzustand Phi also in der Mitte verharrt). Anschließend könnten wir die oberen rechten Kanten abschwächen (k = 0.4), sodass die „Neckerwürfel von unten“-Interpretation die Überhand gewinnt (d.h. Phi zum linken Attraktor strebt). In einem linearen System würde nun ein Rückgängigmachen dieser Parameteränderung (zurück zu k = 0 bzw. gleich starke Würfelkanten) auch zu einer Rückkehr des Systemzustands zum Anfangszustand führen (also Phi = 0). Da bei nichtlinearen Systemen aber die Vorgeschichte eine zentrale Rolle spielt, kann diese Änderung nicht einfach wieder durch k rückgängig gemacht werden, wie man im untersten Teil der Abbildung sieht. Stattdessen bewegt sich Phi nur minimal zum leicht verschobenen linken Attraktor und die Interpretation „Neckerwürfel von unten“ bleibt trotz mehrdeutiger Präsentation (k = 0) erhalten. Wir können in diesem System also für k = 0 zwei (und in Abhängigkeit des Zeitverlaufs viele weitere) Systemzustände beobachten, auch wenn alle anderen Parameter des Modells konstant gehalten werden. | ||
[[File:Attraktormodelle 08.png|center|500px]] | [[File:Attraktormodelle 08.png|center|500px|link=Ausgelagerte_Bildbeschreibungen#Attraktormodelle|Ausgelagerte Bildbeschreibung von Attraktormodelle]] | ||
== Nützliche Links == | == Nützliche Links == | ||
Eine sehr anschauliche Einführung in dynamische Attraktormodelle mit vielen Möglichkeiten zum Ausprobieren bietet die [https://ncase.me/attractors/ Seite] des Videospiel-Designers Nicky Case | Eine sehr anschauliche Einführung in dynamische Attraktormodelle mit vielen Möglichkeiten zum Ausprobieren bietet die [https://ncase.me/attractors/ Seite] des Videospiel-Designers Nicky Case | ||
Aktuelle Version vom 29. März 2022, 12:50 Uhr
Differentialgleichungen werden häufig dafür verwendet, das Verhalten von dynamischen Systemen zu beschreiben. Unter dynamischen Systemen versteht man mathematische Modelle von zeitabhängigen Prozessen, in denen die weitere Entwicklung des Systems vom jeweiligen Anfangszustand abhängt. Mit ihnen kann man bspw. die Bewegung eines Pendels, Klima- oder Populationsveränderungen inklusive Räuber-Beute Interaktionen, aber auch kognitive Prozesse der Wahrnehmung und Entscheidung modellieren.
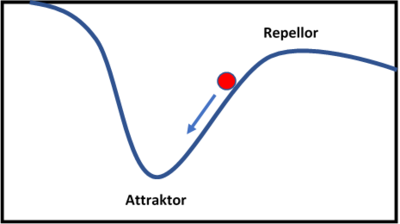
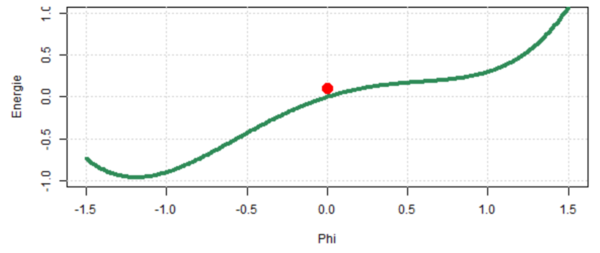
Eine spezielle Gruppe von dynamischen Modellen sind Attraktormodelle. Systeme mit einem Attraktor weisen eine gewisse Anzahl an Zuständen auf, an die sich ein dynamisches System im Laufe der Zeit annähert und dort schließlich verharrt. Nehmen wir an, ein dynamisches System hat genau eine Variable, die sich über die Zeit so verändert, wie es die entsprechende Differentialgleichung beschreibt. Diese Veränderung wird oft über eine sogenannte Potentiallandschaft oder Energielandschaft dargestellt. So sieht man in dem Beispieldiagramm unten das Veränderungspotential oder die Energie für jeden möglichen Zustand des Systems, also jeden möglichen Wert der Variable. Der aktuelle Zustand der Variable wird in dieser Potentiallandschaft als rote Kugel repräsentiert. Die Potentiallandschaft selbst gleicht einer Berg-Tal Landschaft und beschreibt, wie sich der aktuelle Zustand laut der Differentialgleichung ändern wird. Intuitiv gelesen bewegt sich der Ball von den Bergen in das nächstgelegene Tal. Wenn der Ball im Tal angekommen ist, spricht man von einem stabilen Systemzustand – er hat also kein Änderungspotential mehr, im Gegensatz zu den Bergen, bei welchen ein großes Potential zur Veränderung besteht. Stabile Systemzustände können auch komplexere Muster sein, als nur in einem Zustand zu verharren – also z.B. Zyklen von Zuständen. Da der Ball von den Tälern, also den stabilen Zuständen angezogen wird, nennt man diese Zustände auch Attraktoren.
Typische Attraktoren sind also:
- Stabile Fixpunkte: Das System nähert sich - wenn die Zeit gegen unendlich geht - immer stärker einem bestimmten Endzustand an, indem die Dynamik allmählich nachlässt.
- Stabile Zyklen: Hier ist der Endzustand kein einziger Zustand, sondern eine Abfolge immer gleicher Zustände, die sich periodisch abwechseln (Z.B. Räuber-Beute-Modell)
Das Gegenteil von einem Attraktor – die Bergespitzen sozusagen - nennt man Repellor, also einen Zustand, von dem sich das System wegbewegt.
Beispiel: Modell von Tuller et al. (1994)
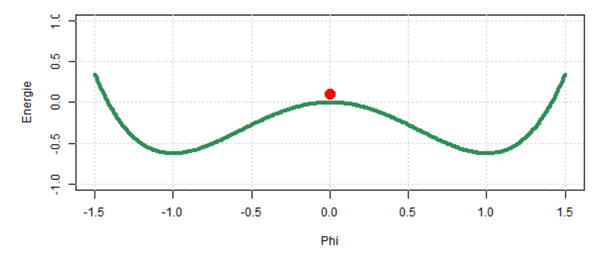
Ein Beispiel für ein Attraktormodell aus der Psychologie ist das Wahrnehmungsmodell von Tuller und Kollegen. Sie stellten 1994 ein Modell zur Beschreibung der dynamischen Kategorisierung von gesprochenen Wörtern auf um zum Beispiel erklären zu können, unter welchen Umständen man das Wort „say“ oder „stay“ hört. Dabei verwendeten Sie eine spannende Manipulation: wenn man bei dem Wort „say“ zwischen s und a eine Lücke einbaut, dann hört man unter Umständen das Wort „stay“. Je größer die Lücke, desto stärker wir die Wahrnehmung von „stay“, je kleiner, desto eher hört man „say“. Es gibt also Länge der Lücke, bei der die beiden Wahrnehmungen gleich stark sind. Hier setzt das Modell an. Beide Wahrnehmungen sind in dem Modell potentiell stabile Zustände mit jeweils eigenem Attraktor, wie es in der Potentiallandschaft dargestellt ist.
Die Variable Phi repräsentiert dabei alle möglichen Zustände, die das System einnehmen kann: also unterschiedliche Grade der eindeutigen Interpretation als „say“ (Phi = -1) oder als „stay“ (Phi = 1). Der Startzustand, also der Zustand in dem Moment, wo man den Stimulus hört, ist neutral (Phi = 0, hier als momentaner Zustand wo die rote Kugel liegt). Das Modell beschreibt nun die Dynamik des Kategorisierungsprozesses über die folgende Gleichung (aus der die gezeigte Potentiallandschaft hergeleitet wird):
Um die Veränderung des Systemzustands über die Zeit berechnen zu können benötigen wir die Ableitung dieser Funktion:
Die Veränderung von Phi über die Zeit können wir dann durch folgende Differentialgleichung beschreiben:
Die Parameter k und s sind wesentlich für die Form der Potentiallandschaft: der Parameter k bestimmt, wie stabil die beiden Zustände „say“ und „stay“ relativ zueinander sind. Er spiegelt im obigen Experiment also die Länge der Lücke zwischen den Buchstaben s und a wider. Ist sie kurz, dann ist der Attraktor bei Phi = -1 stärker ausgeprägt, ist sie lang, dann ist der Attraktor bei Phi = 1 stärker ausgeprägt. Der Parameter s bestimmt, wie tief die Attraktoren an sich sind, wie sehr also das System dazu tendiert, den uneindeutigen Input schnell in eine Kategorie einzuteilen, also schnell in einen Attraktor „zu rutschen“.
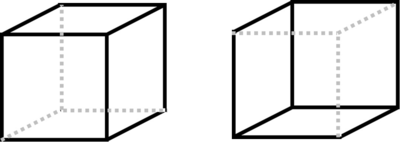
Dieses Modell kann nun nicht nur zur Modellierung der Kategorisierung von „say“ und „stay“ verwendet werden, sondern auch auf alle anderen mehrdeutigen Stimuli angewandt werden, z.B. die Wahrnehmung des Neckerwürfels:
Auch hier können wir zwei stabile Wahrnehmungszustände annehmen, einen „Ich sehe den Würfel von oben“ (links) und einen „Ich sehe den Würfel von unten“ (rechts). Analog zum „say“-„stay“ Beispiel können wir experimentell bestimmte Kanten des Würfels heller oder dunkler machen, was wieder der Parameter k abbilden würde und zu unterschiedlich tiefen Attraktoren führen würde.
kkk Für ein besseres Verständnis der beiden Parameter steht die Webapp Dynamische Attraktormodelle zur Verfügung.
Dort ist es möglich den dynamischen Prozess einer perzeptuellen Entscheidung („Welche Seite des Neckerwürfels sehe ich vorne?“) über eine Animation zu beobachten und durch Manipulation diverser Parameter zu beeinflussen, zum Beispiel wie sehr Rauschen den Prozess beeinflusst und wie einfach eine Wahrnehmung durch eine Störung des Prozesses (Perturbation) beeinflusst werden kann.
Eigenschaften dynamischer Modelle
Am Beispiel des Modells von Tuller et al. können wir viele typische Eigenschaften dynamischer Modelle erkennen:
Multistabilität: Es existieren mehrere Attraktoren mit unterschiedlichen Attraktorbecken gleichzeitig, d.h., mehrere Endzustände sind je nach Ausgangszustand möglich.
Bifurkation: Darunter versteht man eine qualitative Zustandsänderung eines nichtlinearen Systems unter dem Einfluss eines Parameters. Ein nichtlineares System hat einen Output (z.B. eine Wahrnehmung oder ein Verhalten), das nicht immer proportional zum Input (z.B. einem Reiz) ist - im Gegensatz zu einem linearen System. Das bedeutet, dass eine Vergrößerung des Inputs mal zu mehr und mal zu weniger Output führt. Daher können diese Systeme ihr Verhalten also sehr stark ändern, obwohl sich der Input nur minimal verändert hat .
Wenn wir z.B. k (den Input) schrittweise erhöhen, im Experiment mit dem Necker-Würfel also die rechten vorderen Kanten des Würfels weniger sichtbar machen, dann verschiebt sich das Gewicht der beiden Attraktoren so, dass der linke Attraktor (Wahrnehmung: „Neckerwürfel von unten“) im Vergleich zum rechten (Wahrnehmung: „Neckerwürfel von oben“) immer stärker wird. Bei einer bestimmten Ausprägung von k (der relativen Sichtbarkeit der verschiedenen Würfelkanten) führt nun jede noch so minimale weitere Änderung des Parameters (also z.B. eine weitere minimale Ausblendung der Würfelkanten) dazu, dass es nur noch ein statt zwei Attraktorbecken gibt (es könnte nur noch eine Richtung des Würfels gesehen werden). Dieser Übergang von einem (multistabilen) System mit 2 Attraktoren zu einem monostabilen System mit nur einem Attraktor bezeichnet man als Bifurkation – ebenso wie die Gegenrichtung, wenn aus einem monostabilen System ein bistabiles System wird.
Das spannende an der Bifurkation ist, dass hier die Nichtlinearität des Systems zum Tragen kommt. Im Vergleich zu den vorherigen Parameterveränderungen, können wir also mit der gleichen Schrittweite das System jetzt in seiner Qualität (ein statt zwei Attraktoren) deutlich verändern. Die Auswirkungen dieser Nichtlinearität und der dadurch entstehenden Bifurkationen spiegelt sich als Verhalten in der sogenannten Hysterese wider.
Hysterese charakterisiert ein Systemverhalten, bei dem die Ausgangsgröße (z.B. Wahrnehmung oder Verhalten) nicht allein von der Eingangsgröße (z.B. dem Reiz) abhängt, sondern auch vom vorherigen Zustand der Ausgangsgröße (z.B. der Wahrnehmung im letzten Moment). Das System kann also in Abhängigkeit seiner Vorgeschichte bei gleicher Eingangsgröße mehrere Zustände einnehmen – dies nennt man auch Pfadabhängigkeit; man könnte auch sagen es besitzt ein „Gedächtnis“.
In unserem Beispiel könnten wir im Experiment den Neckerwürfel zunächst mit gleich starken Kanten präsentieren (im Modell k = 0, siehe Abbildung), sodass keine Interpretation sich durchsetzt (der Systemzustand Phi also in der Mitte verharrt). Anschließend könnten wir die oberen rechten Kanten abschwächen (k = 0.4), sodass die „Neckerwürfel von unten“-Interpretation die Überhand gewinnt (d.h. Phi zum linken Attraktor strebt). In einem linearen System würde nun ein Rückgängigmachen dieser Parameteränderung (zurück zu k = 0 bzw. gleich starke Würfelkanten) auch zu einer Rückkehr des Systemzustands zum Anfangszustand führen (also Phi = 0). Da bei nichtlinearen Systemen aber die Vorgeschichte eine zentrale Rolle spielt, kann diese Änderung nicht einfach wieder durch k rückgängig gemacht werden, wie man im untersten Teil der Abbildung sieht. Stattdessen bewegt sich Phi nur minimal zum leicht verschobenen linken Attraktor und die Interpretation „Neckerwürfel von unten“ bleibt trotz mehrdeutiger Präsentation (k = 0) erhalten. Wir können in diesem System also für k = 0 zwei (und in Abhängigkeit des Zeitverlaufs viele weitere) Systemzustände beobachten, auch wenn alle anderen Parameter des Modells konstant gehalten werden.
Nützliche Links
Eine sehr anschauliche Einführung in dynamische Attraktormodelle mit vielen Möglichkeiten zum Ausprobieren bietet die Seite des Videospiel-Designers Nicky Case