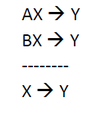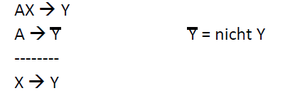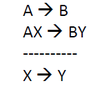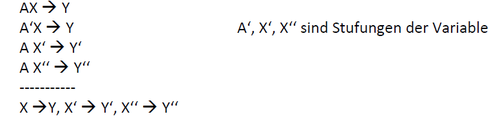Regeln induktiver Erkenntnis nach John Stuart Mill: Unterschied zwischen den Versionen
Diana (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{Nav|Navigation|Erkenntniswege|Wissenschaftstheorie}} John Stuart Mill formulierte eine Reihe von Methoden, die als Regeln für logisch basiertes Induktion…“) |
Paul (Diskussion | Beiträge) (Methode der begleitenden Veränderungen link einfügen pb) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
John Stuart Mill formulierte eine Reihe von Methoden, die als Regeln für logisch basiertes [[Induktion|induktives Schließen]] aufgefasst werden können: | John Stuart Mill formulierte eine Reihe von Methoden, die als Regeln für logisch basiertes [[Induktion|induktives Schließen]] aufgefasst werden können: | ||
<br/>[[Datei:Mill1.png|100px|links]]Die '''Methode der Übereinstimmung''' postuliert: Wenn AX zu Y führt und BX zu Y führt, kann man schließen, dass X zu Y führt. | <br/>[[Datei:Mill1.png|100px|links|link=Ausgelagerte_Bildbeschreibungen#Methode_der_Übereinstimmung|Ausgelagerte Bildbeschreibung von Methode der Übereinstimmung]]Die '''Methode der Übereinstimmung''' postuliert: Wenn AX zu Y führt und BX zu Y führt, kann man schließen, dass X zu Y führt. | ||
''Beispiel: Wenn eine Glühbirne in Lampe A kein Licht erzeugt und in Lampe B auch nicht, kann man davon ausgehen, dass die Glühbirne kaputt ist. '' | ''Beispiel: Wenn eine Glühbirne in Lampe A kein Licht erzeugt und in Lampe B auch nicht, kann man davon ausgehen, dass die Glühbirne kaputt ist. '' | ||
<br/> [[Datei:Mill2.png|300px|links]]Die '''Methode des Unterschieds''' besagt: Wenn AX zu Y führt, aber A alleine nicht, kann man schließen, dass X zu Y führt. | <br/> [[Datei:Mill2.png|300px|links|link=Ausgelagerte_Bildbeschreibungen#Methode_des_Unterschieds|Ausgelagerte Bildbeschreibung von Methode des Unterschieds]]Die '''Methode des Unterschieds''' besagt: Wenn AX zu Y führt, aber A alleine nicht, kann man schließen, dass X zu Y führt. | ||
''Beispiel: Wenn ich Steak und Salat esse und eine Lebensmittelvergiftung kriege, aber meine Tischnachbarin, die nur das Steak aß, nicht – dann kann ich begründet vermuten, dass etwas mit dem Salat nicht gestimmt hat. '' | ''Beispiel: Wenn ich Steak und Salat esse und eine Lebensmittelvergiftung kriege, aber meine Tischnachbarin, die nur das Steak aß, nicht – dann kann ich begründet vermuten, dass etwas mit dem Salat nicht gestimmt hat. '' | ||
<br/>[[Datei:Mill3.png|100px|links]] | <br/>[[Datei:Mill3.png|100px|links|link=Ausgelagerte_Bildbeschreibungen#Methode der Resterscheinung|Ausgelagerte Bildbeschreibung von Methode der Resterscheinung]] | ||
Die '''Methode der Resterscheinungen''' besagt: Wenn A zu B führt und AX zu BY führt, kann man schließen, dass X zu Y führt. | Die '''Methode der Resterscheinungen''' besagt: Wenn A zu B führt und AX zu BY führt, kann man schließen, dass X zu Y führt. | ||
''Beispiel: Wenn ich mit offenem Fenster schlafe, bekomme ich Kopfweh. Schlafe ich zusätzlich ohne Kopfkissen, habe ich Nackenschmerzen und Kopfweh. Vermutlich sind die Nackenschmerzen somit vom fehlenden Kopfkissen ausgelöst. '' | ''Beispiel: Wenn ich mit offenem Fenster schlafe, bekomme ich Kopfweh. Schlafe ich zusätzlich ohne Kopfkissen, habe ich Nackenschmerzen und Kopfweh. Vermutlich sind die Nackenschmerzen somit vom fehlenden Kopfkissen ausgelöst. '' | ||
<br/>[[Datei:Mill4.png|500px|rechts]]Die '''Methode der begleitenden Veränderungen''' besagt: Wenn AX zu Y führt und die Steigerung von AX zum gleichen Y, aber die Steigerung von X zu einer gleichförmigen Steigerung von Y – dann kann man schließen, dass X zu Y führt und beide in ihrer Ausprägung korreliert sind. | <br/>[[Datei:Mill4.png|500px|rechts|link=Ausgelagerte_Bildbeschreibungen#Methode_der_begleitenden_Veränderungen |Ausgelagerte Bildbeschreibung von Methode der begleitenden Veränderungen]]Die '''Methode der begleitenden Veränderungen''' besagt: Wenn AX zu Y führt und die Steigerung von AX zum gleichen Y, aber die Steigerung von X zu einer gleichförmigen Steigerung von Y – dann kann man schließen, dass X zu Y führt und beide in ihrer Ausprägung korreliert sind. | ||
''Beispiel: Nehmen wir an, es macht mich müde, Chips vor dem Fernseher zu essen. Mehr Chips zu essen hat auf die Müdigkeit keinen Einfluss. Je länger ich jedoch fernsehe, desto müder werde ich. Der Schluss liegt somit nahe, dass das Fernsehen die Müdigkeit auslöst und beide in ihrer Intensität korreliert sind. '' | ''Beispiel: Nehmen wir an, es macht mich müde, Chips vor dem Fernseher zu essen. Mehr Chips zu essen hat auf die Müdigkeit keinen Einfluss. Je länger ich jedoch fernsehe, desto müder werde ich. Der Schluss liegt somit nahe, dass das Fernsehen die Müdigkeit auslöst und beide in ihrer Intensität korreliert sind. '' | ||
Aktuelle Version vom 7. Dezember 2021, 16:04 Uhr
John Stuart Mill formulierte eine Reihe von Methoden, die als Regeln für logisch basiertes induktives Schließen aufgefasst werden können:
Die Methode der Übereinstimmung postuliert: Wenn AX zu Y führt und BX zu Y führt, kann man schließen, dass X zu Y führt.
Beispiel: Wenn eine Glühbirne in Lampe A kein Licht erzeugt und in Lampe B auch nicht, kann man davon ausgehen, dass die Glühbirne kaputt ist.
Die Methode des Unterschieds besagt: Wenn AX zu Y führt, aber A alleine nicht, kann man schließen, dass X zu Y führt.
Beispiel: Wenn ich Steak und Salat esse und eine Lebensmittelvergiftung kriege, aber meine Tischnachbarin, die nur das Steak aß, nicht – dann kann ich begründet vermuten, dass etwas mit dem Salat nicht gestimmt hat.
Die Methode der Resterscheinungen besagt: Wenn A zu B führt und AX zu BY führt, kann man schließen, dass X zu Y führt. Beispiel: Wenn ich mit offenem Fenster schlafe, bekomme ich Kopfweh. Schlafe ich zusätzlich ohne Kopfkissen, habe ich Nackenschmerzen und Kopfweh. Vermutlich sind die Nackenschmerzen somit vom fehlenden Kopfkissen ausgelöst.
Die Methode der begleitenden Veränderungen besagt: Wenn AX zu Y führt und die Steigerung von AX zum gleichen Y, aber die Steigerung von X zu einer gleichförmigen Steigerung von Y – dann kann man schließen, dass X zu Y führt und beide in ihrer Ausprägung korreliert sind.
Beispiel: Nehmen wir an, es macht mich müde, Chips vor dem Fernseher zu essen. Mehr Chips zu essen hat auf die Müdigkeit keinen Einfluss. Je länger ich jedoch fernsehe, desto müder werde ich. Der Schluss liegt somit nahe, dass das Fernsehen die Müdigkeit auslöst und beide in ihrer Intensität korreliert sind.