Robustheitsuntersuchungen: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{Nav|Navigation|Statistik|Hauptseite}}“) |
Nadia1 (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation| | {{Nav|Navigation|Statistik_Grundbegriffe|Hauptseite}} | ||
Mithilfe von Robustheitsuntersuchungen kann festgestellt werden, ob statistische Tests trotz verletzter Voraussetzungen anwendbar sind. Das spielt vor allem bei der Vorbereitung empirischer Untersuchungen eine wichtige Rolle. | |||
Bei vielen empirischen Untersuchungen kann nicht davon ausgegangen werden, dass alle Voraussetzungen eines parametrischen Tests erfüllt sind. Es ist jedoch davon abzuraten, einen statistischen Test bei nicht erfüllten Voraussetzungen (wie z.B. Verteilungsannahmen) prinzipiell nicht durchzuführen, da häufig trotzdem robuste Ergebnisse erzielt werden. Ein Test ist dann robust, wenn die Wahrscheinlichkeit für einen Fehler 1. Art ein gegebenes Signifikanzniveau α nicht überschreitet, obwohl nicht alle Voraussetzungen des berechneten Tests erfüllt werden. | |||
Um die Robustheit eines Tests bei verletzten Voraussetzungen zu untersuchen, können Monte-Carlo Studien durchgeführt werden. Dabei werden z.B. aus einer nichtnormalverteilten Grundgesamtheit unter der Annahme der Nullhypothese sehr viele Stichproben des Umfangs n gezogen. Für jede dieser gezogenen Stichproben wird dann ein Signifikanztest – zum Beispiel ein t-Test - mit einem vorher festgelegten Signifikanzniveau α gerechnet. Anschließend berechnet man den Anteil aller Tests, welche die Nullhypothese fälschlicherweise signifikant ablehnen (γ). Handelt es sich um einen robusten Test würde man erwarten, dass γ in etwa gleich hoch ist wie α. Bei γ < α agiert der Test konservativ, d.h. die Nullhypothese wird seltener abgelehnt als erwartet. Grundsätzlich spricht in diesem Fall nichts gegen die Anwendung des Tests, allerdings wird die Wahrscheinlichkeit eines Fehlers 2. Art erhöht und damit die [[Teststärke]] verringert. Bei γ > α wird die Nullhypothese mit größerer Wahrscheinlichkeit als α abgelehnt, d.h. es ist bei einem signifikanten Ergebnis nicht mehr erkennbar, ob tatsächlich ein signifikanter Effekt vorliegt oder ob das signifikante Testergebnis auf die nicht erfüllten Voraussetzungen zurückzuführen ist. In diesem Fall kann der Test nicht angewendet werden. Bei γ 󠆣≈ α entspricht der Anteil abgelehnten Nullhypothesen annähernd der erwarteten Anzahl, d.h. der Test kann trotz verletzter Voraussetzungen ohne Bedenken verwendet werden. | |||
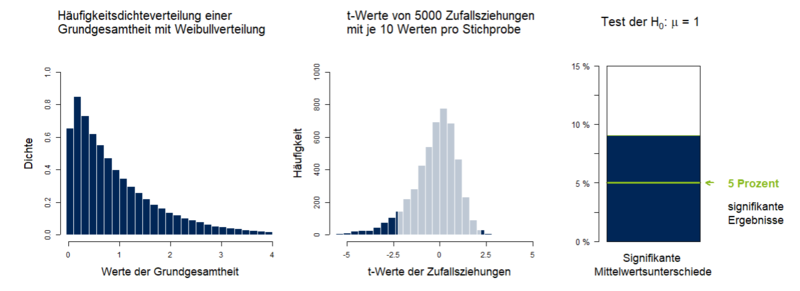
In Abbildung 1 wird eine Robustheitsuntersuchung des t-Tests bei linkssteilen, weibullverteilten Daten (Skalierungsparameter λ = 1, Formparameter k = 1) in Form einer Monte-Carlo Simulation für n = 10 und α = 0.05 dargestellt. | |||
[[File:1_9_Robustheitsuntersuchungen.PNG|800px|Abbildung 1: Monte-Carlo Simulation weibullverteilter Daten|link=Ausgelagerte_Bildbeschreibungen#Robustheitsuntersuchungen|Ausgelagerte Bildbeschreibung von Robustheitsuntersuchungen]] | |||
Im rechten Teil der Abbildung werden die t-Werte aus den Zufallsziehungen sowie der Anteil signifikant abgelehnter Nullhypothesen (γ) dargestellt. Mit einem γ von ca. 9 % werden deutlich mehr Nullhypothesen signifikant abgelehnt als erwartet (0.09 > 0.05). Bei der vorliegenden Verletzung der Annahme der Normalverteilung und beim untersuchten Stichprobenumfang ist der t-Test nicht robust und sollte dementsprechend nicht verwendet werden. Durch Erhöhung des Stichprobenumfanges nähert sich γ auch bei schiefen Verteilungen wie der Weibull-Verteilung α an, der t-Test wird entsprechend robuster. | |||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_9_Robustheitsuntersuchungen_Link.html | |||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_9_Robustheitsuntersuchungen_Link.html Video] werden Robustheitsuntersuchungen näher erläutert. | |||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_9_Robustheitsuntersuchungen/ | |||
|120px]] <span style="color: white"> kkk </span> In der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_9_Robustheitsuntersuchungen/ interaktiven Simulation] lassen sich Monte-Carlo Simulationen für verschiedene Verteilungen mit unterschiedlichen Stichprobenumfängen berechnen. | |||
'''''Weiterführende Literatur''''' | |||
Rudolf, M. & Kuhlisch, W. (2020). ''Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler'' (2. Aufl.). München: Pearson Studium. (Kapitel 6.5) | |||
Aktuelle Version vom 28. Februar 2023, 10:29 Uhr
Mithilfe von Robustheitsuntersuchungen kann festgestellt werden, ob statistische Tests trotz verletzter Voraussetzungen anwendbar sind. Das spielt vor allem bei der Vorbereitung empirischer Untersuchungen eine wichtige Rolle.
Bei vielen empirischen Untersuchungen kann nicht davon ausgegangen werden, dass alle Voraussetzungen eines parametrischen Tests erfüllt sind. Es ist jedoch davon abzuraten, einen statistischen Test bei nicht erfüllten Voraussetzungen (wie z.B. Verteilungsannahmen) prinzipiell nicht durchzuführen, da häufig trotzdem robuste Ergebnisse erzielt werden. Ein Test ist dann robust, wenn die Wahrscheinlichkeit für einen Fehler 1. Art ein gegebenes Signifikanzniveau α nicht überschreitet, obwohl nicht alle Voraussetzungen des berechneten Tests erfüllt werden.
Um die Robustheit eines Tests bei verletzten Voraussetzungen zu untersuchen, können Monte-Carlo Studien durchgeführt werden. Dabei werden z.B. aus einer nichtnormalverteilten Grundgesamtheit unter der Annahme der Nullhypothese sehr viele Stichproben des Umfangs n gezogen. Für jede dieser gezogenen Stichproben wird dann ein Signifikanztest – zum Beispiel ein t-Test - mit einem vorher festgelegten Signifikanzniveau α gerechnet. Anschließend berechnet man den Anteil aller Tests, welche die Nullhypothese fälschlicherweise signifikant ablehnen (γ). Handelt es sich um einen robusten Test würde man erwarten, dass γ in etwa gleich hoch ist wie α. Bei γ < α agiert der Test konservativ, d.h. die Nullhypothese wird seltener abgelehnt als erwartet. Grundsätzlich spricht in diesem Fall nichts gegen die Anwendung des Tests, allerdings wird die Wahrscheinlichkeit eines Fehlers 2. Art erhöht und damit die Teststärke verringert. Bei γ > α wird die Nullhypothese mit größerer Wahrscheinlichkeit als α abgelehnt, d.h. es ist bei einem signifikanten Ergebnis nicht mehr erkennbar, ob tatsächlich ein signifikanter Effekt vorliegt oder ob das signifikante Testergebnis auf die nicht erfüllten Voraussetzungen zurückzuführen ist. In diesem Fall kann der Test nicht angewendet werden. Bei γ 󠆣≈ α entspricht der Anteil abgelehnten Nullhypothesen annähernd der erwarteten Anzahl, d.h. der Test kann trotz verletzter Voraussetzungen ohne Bedenken verwendet werden.
In Abbildung 1 wird eine Robustheitsuntersuchung des t-Tests bei linkssteilen, weibullverteilten Daten (Skalierungsparameter λ = 1, Formparameter k = 1) in Form einer Monte-Carlo Simulation für n = 10 und α = 0.05 dargestellt.
Im rechten Teil der Abbildung werden die t-Werte aus den Zufallsziehungen sowie der Anteil signifikant abgelehnter Nullhypothesen (γ) dargestellt. Mit einem γ von ca. 9 % werden deutlich mehr Nullhypothesen signifikant abgelehnt als erwartet (0.09 > 0.05). Bei der vorliegenden Verletzung der Annahme der Normalverteilung und beim untersuchten Stichprobenumfang ist der t-Test nicht robust und sollte dementsprechend nicht verwendet werden. Durch Erhöhung des Stichprobenumfanges nähert sich γ auch bei schiefen Verteilungen wie der Weibull-Verteilung α an, der t-Test wird entsprechend robuster.
kkk Im Video werden Robustheitsuntersuchungen näher erläutert.
kkk In der interaktiven Simulation lassen sich Monte-Carlo Simulationen für verschiedene Verteilungen mit unterschiedlichen Stichprobenumfängen berechnen.
Weiterführende Literatur
Rudolf, M. & Kuhlisch, W. (2020). Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler (2. Aufl.). München: Pearson Studium. (Kapitel 6.5)