Die t-Verteilung: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Nadia1 (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation| | {{Nav|Navigation|Statistik_Grundbegriffe|Hauptseite}} | ||
Die t-Verteilung oder auch Studentische t-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, die in der Teststatistik im Rahmen unterschiedlicher t-Tests, v.a. bei Mittelwertvergleichen, eine wichtige Rolle spielt. | Die t-Verteilung oder auch Studentische t-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, die in der Teststatistik im Rahmen unterschiedlicher t-Tests, v.a. bei Mittelwertvergleichen, eine wichtige Rolle spielt. | ||
Die t-Verteilung entsteht dadurch, dass aus einer Grundgesamtheit mit den Parametern µ und σ wiederholt Stichproben der Größe n gezogen werden. Für jede dieser Stichproben wird mithilfe der folgenden Formel ein t-Wert bestimmt: | Die t-Verteilung entsteht dadurch, dass aus einer Grundgesamtheit mit den Parametern µ und σ wiederholt Stichproben der Größe n gezogen werden. Für jede dieser Stichproben wird mithilfe der folgenden Formel ein t-Wert bestimmt: | ||
[[File:1_3_1_tVerteilung_Formel.PNG|80px]] | [[File:1_3_1_tVerteilung_Formel.PNG|80px|link=Ausgelagerte_Formeln#t-Wert|Ausgelagerte Formel t-Wert]] | ||
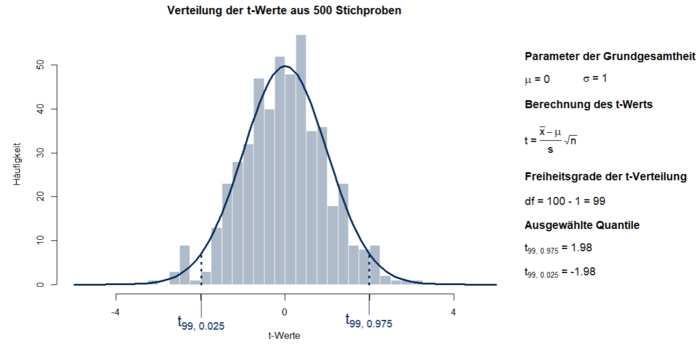
Die dabei entstehenden t-Werte streuen symmetrisch um den Wert 0 (vgl. Abbildung 1). | Die dabei entstehenden t-Werte streuen symmetrisch um den Wert 0 (vgl. Abbildung 1). | ||
[[File:1_3_1_t_Verteilung.PNG| | |||
[[File:1_3_1_t_Verteilung.PNG|700px|Abbildung 1: t-Verteilung, simuliert aus 500 Stichproben der Größe 100|link=Ausgelagerte_Bildbeschreibungen#Die t-Verteilung|Ausgelagerte Bildbeschreibung von Die t-Verteilung]] | |||
Die t-Verteilung ist zunächst breiter als die Standardnormalverteilung, wird mit steigender Anzahl an Freiheitsgraden df = (n-1) jedoch schmaler und nähert sich zunehmend der Form einer Standardnormalverteilung an. | Die t-Verteilung ist zunächst breiter als die Standardnormalverteilung, wird mit steigender Anzahl an Freiheitsgraden df = (n-1) jedoch schmaler und nähert sich zunehmend der Form einer Standardnormalverteilung an. | ||
| Zeile 15: | Zeile 16: | ||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_3_1_t_Verteilung_Link.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_3_1_t_Verteilung_Link.html Video] wird die t-Verteilung näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_3_1_t_Verteilung/ | ||
|120px]] <span style="color: white"> kkk </span> Wie die t-Verteilung entsteht und sich mit zunehmender Stichprobengröße verändert, lässt sich in der [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Wie die t-Verteilung entsteht und sich mit zunehmender Stichprobengröße verändert, lässt sich in der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_3_1_t_Verteilung/ interaktiven Simulation] nachvollziehen. | ||
| Zeile 25: | Zeile 26: | ||
'''''Weiterführende Literatur''''' | '''''Weiterführende Literatur''''' | ||
Rudolf, M. | Rudolf, M. & Kuhlisch, W. (2020). ''Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler'' (2. Aufl.). München: Pearson Studium. (Kapitel 3.3 und 6.1) | ||
Aktuelle Version vom 28. Februar 2023, 10:21 Uhr
Die t-Verteilung oder auch Studentische t-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, die in der Teststatistik im Rahmen unterschiedlicher t-Tests, v.a. bei Mittelwertvergleichen, eine wichtige Rolle spielt. Die t-Verteilung entsteht dadurch, dass aus einer Grundgesamtheit mit den Parametern µ und σ wiederholt Stichproben der Größe n gezogen werden. Für jede dieser Stichproben wird mithilfe der folgenden Formel ein t-Wert bestimmt:
Die dabei entstehenden t-Werte streuen symmetrisch um den Wert 0 (vgl. Abbildung 1).
Die t-Verteilung ist zunächst breiter als die Standardnormalverteilung, wird mit steigender Anzahl an Freiheitsgraden df = (n-1) jedoch schmaler und nähert sich zunehmend der Form einer Standardnormalverteilung an. Die Quantile der t-Verteilung und die damit einhergehenden p-Werte beschreiben den Wert, unterhalb dessen ein bestimmter Anteil der Fläche der Verteilung (einseitige Fragestellung) bzw. die Werte, zwischen denen ein bestimmter Anteil der Fläche der Verteilung liegt (zweiseitige Fragestellung). In Abbildung 1 sind die 95%-Quantile bei zweiseitiger Fragestellung dargestellt. Die Quantile können mit Hilfe von Statistik-Programmen berechnet oder entsprechenden Tabellen entnommen werden.
kkk Im Video wird die t-Verteilung näher erläutert.
kkk Wie die t-Verteilung entsteht und sich mit zunehmender Stichprobengröße verändert, lässt sich in der interaktiven Simulation nachvollziehen.
Weiterführende Literatur
Rudolf, M. & Kuhlisch, W. (2020). Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler (2. Aufl.). München: Pearson Studium. (Kapitel 3.3 und 6.1)