Stichprobenumfangsplanung: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Nadia1 (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation| | {{Nav|Navigation|Statistik_Grundbegriffe|Hauptseite}} | ||
Die Stichprobenumfangsplanung spielt eine wichtige Rolle bei der Versuchsplanung. Bei der Auswahl des Stichprobenumfangs ist es von Interesse, eine hohe Genauigkeit der Ergebnisse zu erzielen und gleichzeitig den wirtschaftlichen und organisatorischen Aufwand so gering wie möglich zu halten. Diese beiden Ziele stehen sich entgegen und es muss ein Kompromiss zwischen beiden gefunden werden. | Die Stichprobenumfangsplanung spielt eine wichtige Rolle bei der Versuchsplanung. Bei der Auswahl des Stichprobenumfangs ist es von Interesse, eine hohe Genauigkeit der Ergebnisse zu erzielen und gleichzeitig den wirtschaftlichen und organisatorischen Aufwand so gering wie möglich zu halten. Diese beiden Ziele stehen sich entgegen und es muss ein Kompromiss zwischen beiden gefunden werden. | ||
| Zeile 9: | Zeile 9: | ||
Es wird derjenige Stichprobenumfang ermittelt, der unter gegebenen Signifikanzniveau und Parameterschätzungen eine bestimmte Genauigkeit erzielt. Dieser kann im Fall des Tests auf der Basis der Standardnormalverteilung über die folgende Formel berechnet werden: | Es wird derjenige Stichprobenumfang ermittelt, der unter gegebenen Signifikanzniveau und Parameterschätzungen eine bestimmte Genauigkeit erzielt. Dieser kann im Fall des Tests auf der Basis der Standardnormalverteilung über die folgende Formel berechnet werden: | ||
[[File: | |||
[[File:1_5_formel_neu.PNG|150px|link=Ausgelagerte_Formeln#Stichprobenumfang|Ausgelagerte Formel Stichprobenumfang]] | |||
z<sub>1-β</sub> und z<sub>1-α</sub> sind die Werte der Standardnormalverteilung für das jeweilige Quantil und lassen sich aus entsprechenden Tabellen ablesen. σ entspricht der Streuung und Δ dem Mittelwertsunterschied. | z<sub>1-β</sub> und z<sub>1-α</sub> sind die Werte der Standardnormalverteilung für das jeweilige Quantil und lassen sich aus entsprechenden Tabellen ablesen. σ entspricht der Streuung und Δ dem Mittelwertsunterschied. | ||
'''''Beispiel''''' | '''''Beispiel''''' | ||
| Zeile 19: | Zeile 21: | ||
[[File:1_5_Stichprobenumfangsplanung.PNG| | [[File:1_5_Stichprobenumfangsplanung.PNG|700px|Abbildung 1: Verteilung der Stichprobenmittelwerte zweier Populationen und Darstellung der Teststärke|link=Ausgelagerte_Bildbeschreibungen#Stichprobenumfangsplanung|Ausgelagerte Bildbeschreibung von Stichprobenumfangsplanung]] | ||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_5_Stichprobenumfangsplanung_Link.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/1_5_Stichprobenumfangsplanung_Link.html Video] wird die Stichprobenumfangsplanung näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_5_Stichprobenumfangsplanung/ | ||
|120px]] <span style="color: white"> kkk </span> Wie der Stichprobenumfang von Grundgesamtheiten mit unterschiedlichen Parameterwerten die Teststärke beeinflusst, lässt sich in der [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Wie der Stichprobenumfang von Grundgesamtheiten mit unterschiedlichen Parameterwerten die Teststärke beeinflusst, lässt sich in der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/1_5_Stichprobenumfangsplanung/ interaktiven Simulation] grafisch veranschaulichen. | ||
'''''Weiterführende Literatur''''' | '''''Weiterführende Literatur''''' | ||
Cohen, J. (2013). ''Statistical power analysis for the behavioral sciences''. Routledge. | Cohen, J. (2013). ''Statistical power analysis for the behavioral sciences''. Routledge. | ||
Rudolf, M. | Rudolf, M. & Kuhlisch, W. (2020). ''Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler'' (2. Aufl.). München: Pearson Studium. (Kapitel 9.3) | ||
Aktuelle Version vom 28. Februar 2023, 10:24 Uhr
Die Stichprobenumfangsplanung spielt eine wichtige Rolle bei der Versuchsplanung. Bei der Auswahl des Stichprobenumfangs ist es von Interesse, eine hohe Genauigkeit der Ergebnisse zu erzielen und gleichzeitig den wirtschaftlichen und organisatorischen Aufwand so gering wie möglich zu halten. Diese beiden Ziele stehen sich entgegen und es muss ein Kompromiss zwischen beiden gefunden werden.
Die Genauigkeit der Ergebnisse wird durch die Teststärke (1-β) definiert. Wie hoch diese sein sollte, wird anhand von Vorüberlegungen durch den Anwender festgelegt. In der Praxis wird häufig eine Teststärke von 0.8 bzw. 80 % als akzeptabel vertreten. Es wird also eine Wahrscheinlichkeit von 0.2 bzw. 20 % für einen β-Fehler akzeptiert. Diese ist viermal höher als die oft maximal akzeptierte Irrtumswahrscheinlichkeit für einen α-Fehler (0.05).
Da die Streuung, der Mittelwertsunterschied und das Signifikanzniveau nicht, bzw. nicht ohne Konsequenzen veränderbar sind, stellt die in der Praxis oftmals einzige Stellschraube zur Veränderung der Teststärke der Stichprobenumfang dar. Erhöht man den Stichprobenumfang, verkleinert sich der Standardfehler des Mittelwertes und es erhöht sich die Teststärke, da die Mittelwertsverteilungen der Alternativ- und der Nullhypothese schmaler werden und dadurch weniger überlappen, d.h. besser voneinander abzugrenzen sind.
Es wird derjenige Stichprobenumfang ermittelt, der unter gegebenen Signifikanzniveau und Parameterschätzungen eine bestimmte Genauigkeit erzielt. Dieser kann im Fall des Tests auf der Basis der Standardnormalverteilung über die folgende Formel berechnet werden:
z1-β und z1-α sind die Werte der Standardnormalverteilung für das jeweilige Quantil und lassen sich aus entsprechenden Tabellen ablesen. σ entspricht der Streuung und Δ dem Mittelwertsunterschied.
Beispiel
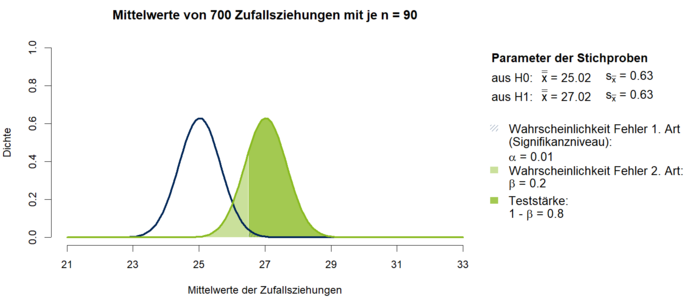
In einem großen Unternehmen soll zur Verbesserung der Arbeitszufriedenheit ein kostenloses Sport- und Entspannungsprogramm für die Mitarbeiter angeboten werden. Die mittlere Arbeitszufriedenheit in diesem Unternehmen beträgt 25 bei einer Standardabweichung von 6. Damit sich der finanzielle Mehraufwand lohnt, sollte das Programm die Arbeitszufriedenheit um mindestens 2 erhöhen. Zur Finanzierung des Programmes ist eine langfristig geplante Umstrukturierung an mehreren Standorten des Unternehmens vorgesehen, falls sich das Programm als erfolgreich herausstellen sollte. Deswegen wird ein konservativeres Signifikanzniveau von 0.01 festgelegt, um das Risiko von Fehlinvestitionen möglichst gering zu halten. Gleichzeitig soll die Wahrscheinlichkeit ein signifikantes Ergebnis zu finden, wenn auch tatsächlich eine Verbesserung der Arbeitszufriedenheit um 2 Punkte vorliegt, mindestens 80 % betragen. Zur Überprüfung der Wirksamkeit soll dieses testweise für einen Teil der Mitarbeiter angeboten werden. Um bei einer Genauigkeit von mindestens 80 % den Kostenaufwand möglichst gering zu halten, wird eine Stichprobenumfangsplanung durchgeführt. Es wird der Stichprobenumfang gesucht, der bei einem Mittelwertsunterschied von Δ = 2 zwischen den Populationen und einer Streuung von σ = 6 bei einem Signifikanztest mit α = 0.01 in 80 % der Fälle ein signifikantes Ergebnis findet. Bei dieser ergibt sich mit der oben genannten Formel, dass unter den gegebenen Parametern (Δ = 2; σ = 6) und einem Signifikanzniveau von α = 0.01 ein Stichprobenumfang von n = 90 erforderlich ist, um einen tatsächlichen Effekt des Programms mit 80 %-iger Wahrscheinlichkeit zu finden. In Abbildung 1 wird der beschriebene Sachverhalt grafisch dargestellt.
kkk Im Video wird die Stichprobenumfangsplanung näher erläutert.
kkk Wie der Stichprobenumfang von Grundgesamtheiten mit unterschiedlichen Parameterwerten die Teststärke beeinflusst, lässt sich in der interaktiven Simulation grafisch veranschaulichen.
Weiterführende Literatur
Cohen, J. (2013). Statistical power analysis for the behavioral sciences. Routledge.
Rudolf, M. & Kuhlisch, W. (2020). Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler (2. Aufl.). München: Pearson Studium. (Kapitel 9.3)