Grundbegriffe Mathematik: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (30 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Zahlenmengen== | ==Zahlenmengen== | ||
Zahlen können einer oder mehreren Mengen angehören. Die wichtigsten Zahlenmengen sind unten beschrieben. Um die Zugehörigkeit einer Zahl auszudrücken, verwendet man das Element-Zeichen ∈, z.B. 5 ∈ N, gesprochen „fünf ist Element der natürlichen Zahlen“. | |||
Zahlen können einer oder mehreren Mengen angehören. Die wichtigsten Zahlenmengen sind unten beschrieben. Um die Zugehörigkeit einer Zahl auszudrücken, verwendet man das Element-Zeichen ∈, z.B. 5 ∈ N, | |||
*'''Natürliche Zahlen:''' Natürliche Zahlen sind die beim Zählen verwendeten Zahlen. Sie sind ganzzahlig (d.h. sie enthalten keine Brüche oder Dezimalstellen) und positiv und beginnen bei eins. Ihr Formelzeichen ist das ℕ<sub>0</sub>. | *'''Natürliche Zahlen:''' Natürliche Zahlen sind die beim Zählen verwendeten Zahlen. Sie sind ganzzahlig (d.h. sie enthalten keine Brüche oder Dezimalstellen) und positiv und beginnen bei eins. Ihr Formelzeichen ist das ℕ<sub>0</sub>. | ||
| Zeile 25: | Zeile 23: | ||
*'''Imaginäre Zahlen:''' Imaginäre Zahlen sind diejenigen komplexen Zahlen, deren Quadrate nicht positive reelle Zahlen sind. D.h. wenn aus einer nicht positiven reellen Zahl eine Wurzel gezogen wird, kommt dabei eine imaginäre Zahl heraus. Geschrieben werden diese Zahlen als Produkt der imaginären Einheit i mit einem reellen Faktor ''b''. Dabei gilt i = <span style="white-space: nowrap"> √<span style="text-decoration:overline;"> -1 </span></span>. | *'''Imaginäre Zahlen:''' Imaginäre Zahlen sind diejenigen komplexen Zahlen, deren Quadrate nicht positive reelle Zahlen sind. D.h. wenn aus einer nicht positiven reellen Zahl eine Wurzel gezogen wird, kommt dabei eine imaginäre Zahl heraus. Geschrieben werden diese Zahlen als Produkt der imaginären Einheit i mit einem reellen Faktor ''b''. Dabei gilt i = <span style="white-space: nowrap"> √<span style="text-decoration:overline;"> -1 </span></span>. | ||
*'''Komplexe Zahlen:''' Mit der Erweiterung der reellen Zahlen zu den komplexen Zahlen wechselt man von der Zahlengeraden zur Zahlenebene | *'''Komplexe Zahlen:''' Mit der Erweiterung der reellen Zahlen zu den komplexen Zahlen wechselt man von der Zahlengeraden zur Zahlenebene. Komplexe Zahlen werden als Summe ''a''+''b''∙i geschrieben, wobei ''a'' und ''b'' reelle Zahlen sind und i die imaginäre Einheit. In dieser Schreibweise gibt a den Wert des reellen Anteils der Zahl und ''b'' den Wert des imaginären Anteils der Zahl an. Man kann sie als Koordinaten auf der Zahlenebene verstehen. Das Formelzeichen der komplexen Zahlen ist ℂ. Mehr findet sich auf der Seite [[Komplexe Zahlen|Komplexe Zahlen]] innerhalb dieses Mediawikis. | ||
[[Datei:Zahlenmengen.PNG|500px|zentriert]] | |||
==Notationen (Auswahl)== | ==Notationen (Auswahl)== | ||
| Zeile 37: | Zeile 37: | ||
*'''Größer und kleiner als:''' Beschreiben, dass der Ausdruck links des Zeichens > größer (< kleiner) ist als der rechts des Zeichens | *'''Größer und kleiner als:''' Beschreiben, dass der Ausdruck links des Zeichens > größer (< kleiner) ist als der rechts des Zeichens | ||
*'''Größer und kleiner gleich:''' Beschreiben, dass der Ausdruck links des Zeichens ≥ größer (& | *'''Größer und kleiner gleich:''' Beschreiben, dass der Ausdruck links des Zeichens ≥ größer (≤ kleiner) oder gleich dem rechten Ausdruck ist | ||
===Rechenoperatoren=== | ===Rechenoperatoren=== | ||
| Zeile 52: | Zeile 52: | ||
*'''Summe:''' Steht für die Summe mehrerer Ausdrücke. Häufig genutzt, um Summen von Termen mit Variablen abzukürzen. Das Zeichen ist ∑ | *'''Summe:''' Steht für die Summe mehrerer Ausdrücke. Häufig genutzt, um Summen von Termen mit Variablen abzukürzen. Das Zeichen ist ∑ | ||
** Beispiel: < | **Beispiel: <math>\sum_{i=1}^{3} 5x_{i} = 5x_{1} + 5x_{2} + 5x_{3}</math> | ||
*'''Produkt:''' Steht für das Produkt mehrerer Ausdrücke. Häufig genutzt, um Produkte von Termen mit Variablen abzukürzen. Das Zeichen ist ∏ | *'''Produkt:''' Steht für das Produkt mehrerer Ausdrücke. Häufig genutzt, um Produkte von Termen mit Variablen abzukürzen. Das Zeichen ist ∏ | ||
**Beispiel: <math>\prod_{i=1}^{3} 5x_{i} = 5x_{1} \cdot 5x_{2} \cdot 5x_{3}</math> | |||
*'''Potenzieren | *'''Potenzieren:''' Die Basis wird wiederholt multipliziert, die Schreibweise ist ''a''<sup>''b''</sup>. Wie oft dabei die Basis (''a'') als Faktor steht, wird durch den Exponenten (''b'') bestimmt. Z.B. 5<sup>3</sup> = 5 · 5 · 5 | ||
* | *'''Logarithmus:''' Der Logarithmus, geschrieben ''b'' = log<sub>''a''</sub>''c'', gibt den Exponenten (''b'') an, mit dem man eine Basis (''a'') potenzieren muss, um den Numerus (''c'') zu erhalten. Z.B. 3 = log<sub>5</sub>125 | ||
= | *'''Wurzel:''' Das Wurzelziehen (auch Radizieren) ist die Umkehrung des Potenzierens und ermittelt die Basis ''a'' aus einer mit ''b'' potenzierten Zahl ''c'', in der Form <math>a = \sqrt[b]{c}</math>, wie zum Beispiel <math>5 = \sqrt[3]{125}</math>. Bei einer Quadratwurzel (''b'' = 2), wird der Exponent häufig freigelassen, z.B. <math>5 = \sqrt{25}</math>. | ||
== | *'''Fakultät:''' Die Fakultät einer Zahl ist das Produkt aller positiven natürlichen Zahlen, die kleiner oder gleich dieser Zahl sind | ||
**Beispiel: 5!= 5 · 4 · 3 · 2 · 1 = 120 | |||
**ein Spezialfall ist 0! = 1 | |||
*'''Binomialkoeffizient:''' Der Binomialkoeffizient <math>\binom{N}{k}</math> (gesprochen „''n'' über ''k''“) gibt an wie viele Kombinationen einer Anzahl von ''k'' Objekten aus einer Menge von ''n'' voneinander unterscheidbaren Objekten gezogen werden kann, ohne die Reihenfolge zu beachten und ohne Zurücklegen. | |||
*'''Betrag:''' Der Betrag einer Zahl ist ihr Abstand zu null. Auch: Absolutwert oder Absolutbetrag. Geschrieben wird er als |''x''|, z.B. |-5.54| = 5.54 | |||
*'''Ableitung:''' Die (erste) Ableitung oder Differentiation einer Funktion bildet die Steigung der Funktion ab. Eine Zusammenfassung mit Ableitungsregeln und Sonderfällen findet sich in der [https://de.wikipedia.org/wiki/Differentialrechnung#Ableitungsberechnung deutschsprachigen Wikipedia]. Notiert wird die Ableitung einer Funktion häufig als <math>f'(x)</math> (Lagrange-Notation) oder <math>\frac{d f(x)}{dx}</math> (Leibniz-Notation, gesprochen "d f von x nach d x"). | |||
*'''Integral:''' Integral ist ein Oberbegriff für bestimmte und unbestimmte Integrale. | |||
** Das '''bestimmte Integral''' einer Funktion ''f'' ist eine Zahl und wird bestimmt genannt, weil es das Integral einer Funktion in einem gegebenen Intervall ist. Zum Beispiel ergibt das Integral einer reellen Funktion ''f''(''x'') im Intervall ''a ≤ x ≤ b'' die Fläche unter dem Funktionsgraphen von ''f''(''x'') in den Intervallgrenzen ''a'' und ''b'' an. Funktionsabschnitte, bei denen ''f''(''x'') < 0 ist, werden negativ in die Flächenberechnung gezählt. Dabei schreibt man <math>\int_{a}^{b} f(x) \,dx</math> | |||
**Das unbestimmte Intervall einer Funktion ''f'' ist ihre Stammfunktion ''F''. Die erste Ableitung von ''F'' ist ''f''. Aufgrund der o.g. Ableitungsregeln hat eine Funktion ''f'' nicht eine einzige Stammfunktion, sondern viele. Beispielsweise sind <math>F(x) = x^{2} + 5</math> und <math>F(x) = x^{2} + 470</math> Stammfunktionen von <math>f(x) = 2x</math>, da Summanden, die nicht die Variable x enthalten, in der Ableitung wegfallen. Die Stammfunktion wird benötigt, um bestimmte Integrale einer Funktion zu berechnen. Dabei gilt <math>\int_{a}^{b} f(x) = F(b) - F(a) \,dx</math>, wobei die rechte Seite verkürzt notiert werden kann als <math>[F(x)]_a^b</math> | |||
=Grundbegriffe der Logik und logische Operatoren= | |||
*'''Proposition:''' eine Aussage oder ein Satz, der wahr oder falsch sein kann, aber nicht beides gleichzeitig. Damit ist die Proposition ein Grundbaustein für die Untersuchung logischer Argumente und Schlussfolgerungen. Das bedeutet, dass jede Proposition eine klare Bedeutung hat, die entweder wahr oder falsch ist, aber nicht beides zugleich. Propositionen werden oft mit Buchstaben wie ''p'', ''q'', ''r'' usw. symbolisiert, um in komplexeren logischen Ausdrücken verwendet zu werden. | |||
*'''Wahrheitswert''': ein logischer Wert, der angibt, ob eine Aussage wahr oder falsch ist, oft mit ''w'' und ''f'' oder ''t'' und ''f'' (true/false) abgekürzt. Wenn man von diesen zwei Wahrheitswerten, also wahr oder falsch ausgeht, spricht man von zweiwertiger Logik. Der Wahrheitswert einer Aussage ist abhängig vom Kontext und den zugrundeliegenden Annahmen oder Prämissen. | |||
* | *'''Verbindung:''' Operator, der Aussagen miteinander verknüpft. Damit können neue Aussagen gebildet und Beziehungen zwischen Aussagen untersucht werden. | ||
**Konjunktion: die Verknüpfung zweier Aussagen durch das logische "UND". Eine Konjunktion ist wahr, wenn beide Aussagen, die sie verknüpft, wahr sind, ansonsten ist sie falsch (false). Ihr Symbol ist ∧ | |||
**Disjunktion: die Verknüpfung zweier Aussagen durch das logische "ODER". Eine Disjunktion ist wahr, wenn mindestens eine der beiden Aussagen, die sie verknüpft, wahr ist; Sie ist nur dann falsch, wenn beide Aussagen falsch sind; ihr Symbol ist ∨ | |||
***exklusive Disjunktion: ist wahr, wenn genau eine der beiden Aussagen, die sie verknüpft, wahr ist, und falsch, wenn beide Aussagen gleichzeitig wahr oder beide gleichzeitig falsch sind. Häufig wird sie mit ⊻ symbolisiert. | |||
**Implikation: eine logische Beziehung zwischen zwei Aussagen, bei der die Wahrheit der ersten Aussage die Wahrheit der zweiten Aussage bestimmt. Die Implikation wird oft mit "wenn..., dann..." ausgedrückt. Ihr Symbol ist → | |||
**Äquivalenz: eine gegenseitige logische Beziehung zwischen zwei Aussagen, bei der beide Aussagen entweder gleichzeitig wahr oder gleichzeitig falsch sind. Eine Äquivalenz zwischen zwei Aussagen wird oft mit dem Begriff "wenn und nur wenn" oder "genau dann, wenn" ausgedrückt. Sie bedeutet, dass die Wahrheit der einen Aussage die Wahrheit der anderen impliziert und umgekehrt. Ihr Symbol ist ⇔ | |||
**Negation: die Verneinung einer Aussage. Sie wird verwendet, um eine Aussage in ihre entgegengesetzte Form umzuwandeln. Ihr Symbol ist ¬ | |||
* | *'''Wahrheitstabelle:''' Methode in der Logik, um alle möglichen Wahrheitswerte einer logischen Verbindung oder Funktion systematisch darzustellen. Sie zeigt alle Kombinationen von Wahrheitswerten für die beteiligten Aussagen und gibt den resultierenden Wahrheitswert der Verbindung an. | ||
**Man identifiziert zuerst alle relevanten Propositionen oder Variablen und jede mögliche Kombination der Wahrheitswerte dieser Propositionen. Bei ''n'' Propositionen gibt es <math>2^{n}</math> Kombinationen von Wahrheitswerten | |||
**Für die einzelnen Kombinationen wird jeweils der Wahrheitswert errechnet und tabellarisch abgetragen | |||
**Beispiel: Es gilt für die Aussagen ''p'' und ''q'' die Konjunktion ''p''∧''q'', das heißt, die Konjunktion wird dann wahr, wenn ''p'' und ''q'' wahr sind. Die Wahrheitstabelle für diesen Fall könnte sein: | |||
{| class="wikitable" style="margin:auto" | |||
|+ Wahrheitstabelle für ''p''∧''q'' | |||
|- | |||
! ''p'' !! ''q'' !! ''p''∧''q'' | |||
|- | |||
| w || w || w | |||
|- | |||
| w || f || f | |||
|- | |||
| f || w || f | |||
|- | |||
| f || f || f | |||
|} | |||
* | *'''Gültigkeit & Korrektheit''' | ||
**Die Gültigkeit eines Arguments oder einer logischen Formel sagt aus, ob die Schlussfolgerung aus den gegebenen Prämissen logisch folgt, sie ist also eine Aussage über die Struktur des Arguments. Die Schlussfolgerung eines gültigen Arguments muss wahr sein, wenn seine Prämissen wahr sind, unabhängig vom tatsächlichen Wahrheitsgehalt der Prämissen oder Schlussfolgerung. | |||
**Die Korrektheit eines Arguments betrifft die Wahrheit der Prämissen und der Schlussfolgerung. Ein korrektes Argument ist, wenn die Prämissen wahr sind und auch die Schlussfolgerung wahr ist. Ein korrektes Argument ist also immer gültig, aber ein gültiges Argument nicht zwingend korrekt. | |||
* | *'''Schlussregeln''': methodische Vorgehensweisen, um aus gegebenen Prämissen logisch gültige Schlussfolgerungen zu ziehen | ||
**Modus ponens (Befolgung): Wenn ''p'' wahr ist und ''p''→''q'' wahr ist, dann ist ''q'' wahr. | |||
**Modus tollens (Verneinung): Wenn ''p''→''q'' wahr ist und ''q'' falsch ist, dann ist ''p'' falsch | |||
**Hypothetischer Syllogismus: Wenn ''p''→''q'' wahr ist und ''q''→''r'' wahr ist, dann ist ''p''→''r'' wahr. | |||
**Disjunktiver Syllogismus: Wenn ''p''∨''q'' wahr ist und ¬''p'' wahr ist, dann ist ''q'' wahr. | |||
**Einführung und Elimination von Konjunktionen: | |||
***Einführung: Wenn ''p'' wahr ist und ''q'' wahr ist, dann ist ''p''∧''q'' wahr. | |||
***Elimination: Wenn ''p''∧''q'' wahr ist, dann sind ''p'' und ''q'' wahr. | |||
**Einführung und Elimination von Disjunktionen: | |||
***Einführung: Wenn ''p'' wahr ist, dann ist ''p''∨''q'' wahr. | |||
***Elimination: Wenn ''p''∨''q'' wahr ist und ''p''→''r'' wahr ist und ''q''→''r'' wahr ist, dann ist ''r'' wahr. | |||
* | *'''Quantor/Quantifikator:''' Ausdruck, der angibt, wie viele oder welche Elemente einer Menge eine bestimmte Eigenschaft erfüllen. Die zwei grundlegensten Quantoren sind: | ||
**Allquantor: sagt aus, dass eine bestimmte Eigenschaft für alle Elemente einer Menge gilt; Symbol: ∀ | |||
**Existenzquantor: sagt aus, dass es mindestens ein Element in einer Menge gibt, für das eine bestimmte Eigenschaft gilt; Symbol: ∃ | |||
Aktuelle Version vom 2. September 2024, 16:28 Uhr
Mathematische Basisoperationen & Formeln lesen
Die Grundbausteine mathematischer Formeln sind Variablen und Konstanten. Sie werden durch Operationen in Verbindung gesetzt. Für bestimmte Ausdrücke werden außerdem Notationen genutzt, die Operationen und Beziehungen von mathematischen Elementen kompakt und standardisiert ausdrücken.
Zahlenmengen
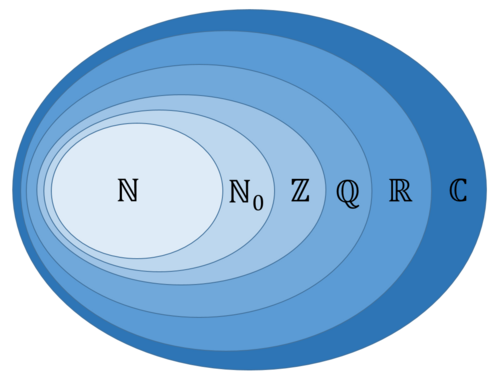
Zahlen können einer oder mehreren Mengen angehören. Die wichtigsten Zahlenmengen sind unten beschrieben. Um die Zugehörigkeit einer Zahl auszudrücken, verwendet man das Element-Zeichen ∈, z.B. 5 ∈ N, gesprochen „fünf ist Element der natürlichen Zahlen“.
- Natürliche Zahlen: Natürliche Zahlen sind die beim Zählen verwendeten Zahlen. Sie sind ganzzahlig (d.h. sie enthalten keine Brüche oder Dezimalstellen) und positiv und beginnen bei eins. Ihr Formelzeichen ist das ℕ0.
- Natürliche Zahlen mit Null: Hier wird die Null in die Menge der natürlichen Zahlen eingeschlossen. Ihr Formelzeichen ist das ℕ.
- Ganze Zahlen: Ganze Zahlen sind die Erweiterung der natürlichen Zahlen um ihre negativen Gegenzahlen. D.h. sie schließen alle positiven und negativen Zahlen ohne Bruch oder Dezimalstellen und die Null ein. Ihr Formelzeichen ist das ℤ.
- Rationale Zahlen: Eine rationale Zahl ist eine reelle Zahl, die durch das Verhältnis von zwei ganzen Zahlen dargestellt werden kann, d.h. sie lassen sich als Bruch oder Dezimalzahl schreiben. Ihr Formelzeichen ist ℚ.
- Irrationale Zahlen: Irrationale Zahlen sind die Menge von reellen, nicht-rationalen Zahlen. Sie sind nicht als Verhältnis zweier ganzer Zahlen darstellbar und werden als Dezimalzahlen mit einer nicht periodischen und unendlichen Anzahl von Dezimalstellen dargestellt. Beispiele sind π und die Eulersche Zahl. Das Formelzeichen der Irrationalen Zahlen ist ℝ\ℚ.
- Reelle Zahlen: Die reellen Zahlen sind die Erweiterung der rationalen Zahlen um die irrationalen Zahlen. Ihr Formelzeichen ist ℝ.
- Imaginäre Zahlen: Imaginäre Zahlen sind diejenigen komplexen Zahlen, deren Quadrate nicht positive reelle Zahlen sind. D.h. wenn aus einer nicht positiven reellen Zahl eine Wurzel gezogen wird, kommt dabei eine imaginäre Zahl heraus. Geschrieben werden diese Zahlen als Produkt der imaginären Einheit i mit einem reellen Faktor b. Dabei gilt i = √ -1 .
- Komplexe Zahlen: Mit der Erweiterung der reellen Zahlen zu den komplexen Zahlen wechselt man von der Zahlengeraden zur Zahlenebene. Komplexe Zahlen werden als Summe a+b∙i geschrieben, wobei a und b reelle Zahlen sind und i die imaginäre Einheit. In dieser Schreibweise gibt a den Wert des reellen Anteils der Zahl und b den Wert des imaginären Anteils der Zahl an. Man kann sie als Koordinaten auf der Zahlenebene verstehen. Das Formelzeichen der komplexen Zahlen ist ℂ. Mehr findet sich auf der Seite Komplexe Zahlen innerhalb dieses Mediawikis.
Notationen (Auswahl)
Vergleichsoperatoren
- Gleichheit: Beschreibt, dass zwei Ausdrücke in ihrem Wert gleich sind und wird durch das Zeichen = repräsentiert, das zwischen den gleichen Ausdrücken steht
- Ungleichheit: Beschreibt, dass zwei Ausdrücke in ihrem Wert ungleich sind und wird durch das Zeichen ≠ repräsentiert, das zwischen den ungleichen Ausdrücken steht
- Größer und kleiner als: Beschreiben, dass der Ausdruck links des Zeichens > größer (< kleiner) ist als der rechts des Zeichens
- Größer und kleiner gleich: Beschreiben, dass der Ausdruck links des Zeichens ≥ größer (≤ kleiner) oder gleich dem rechten Ausdruck ist
Rechenoperatoren
- Addition: Zählt einen Summanden zum anderen hinzu. Das Ergebnis ist die Summe. Das Zeichen ist +
- Subtraktion: Zieht den Subtrahenden (rechte Zahl) vom Minuenden (linke Zahl) ab. Das Ergebnis ist die Differenz. Das Zeichen ist -
- Multiplikation: Bedeutet das Vervielfachen des einen Faktors um den Wert des anderen. Das Ergebnis ist das Produkt. Das Zeichen ist · oder manchmal ×
- Division: Teilt den Zähler bzw. Dividend (obere/linke Zahl) durch den Nenner bzw. Divisor (untere/rechte Zahl). Das Ergebnis ist der Quotient. Das Zeichen ist ÷ oder als Bruchschreibweise z.B. ¼
- Modulo: Modulo berechnet den Rest bei einer Division der Zahl a durch die Zahl b. Häufiger beim Programmieren genutzt. Die Schreibweise ist mod(a,b), z.B. mod(2,5) = 1
- Summe: Steht für die Summe mehrerer Ausdrücke. Häufig genutzt, um Summen von Termen mit Variablen abzukürzen. Das Zeichen ist ∑
- Beispiel:
- Produkt: Steht für das Produkt mehrerer Ausdrücke. Häufig genutzt, um Produkte von Termen mit Variablen abzukürzen. Das Zeichen ist ∏
- Beispiel:
- Potenzieren: Die Basis wird wiederholt multipliziert, die Schreibweise ist ab. Wie oft dabei die Basis (a) als Faktor steht, wird durch den Exponenten (b) bestimmt. Z.B. 53 = 5 · 5 · 5
- Logarithmus: Der Logarithmus, geschrieben b = logac, gibt den Exponenten (b) an, mit dem man eine Basis (a) potenzieren muss, um den Numerus (c) zu erhalten. Z.B. 3 = log5125
- Wurzel: Das Wurzelziehen (auch Radizieren) ist die Umkehrung des Potenzierens und ermittelt die Basis a aus einer mit b potenzierten Zahl c, in der Form , wie zum Beispiel . Bei einer Quadratwurzel (b = 2), wird der Exponent häufig freigelassen, z.B. .
- Fakultät: Die Fakultät einer Zahl ist das Produkt aller positiven natürlichen Zahlen, die kleiner oder gleich dieser Zahl sind
- Beispiel: 5!= 5 · 4 · 3 · 2 · 1 = 120
- ein Spezialfall ist 0! = 1
- Binomialkoeffizient: Der Binomialkoeffizient (gesprochen „n über k“) gibt an wie viele Kombinationen einer Anzahl von k Objekten aus einer Menge von n voneinander unterscheidbaren Objekten gezogen werden kann, ohne die Reihenfolge zu beachten und ohne Zurücklegen.
- Betrag: Der Betrag einer Zahl ist ihr Abstand zu null. Auch: Absolutwert oder Absolutbetrag. Geschrieben wird er als |x|, z.B. |-5.54| = 5.54
- Ableitung: Die (erste) Ableitung oder Differentiation einer Funktion bildet die Steigung der Funktion ab. Eine Zusammenfassung mit Ableitungsregeln und Sonderfällen findet sich in der deutschsprachigen Wikipedia. Notiert wird die Ableitung einer Funktion häufig als (Lagrange-Notation) oder (Leibniz-Notation, gesprochen "d f von x nach d x").
- Integral: Integral ist ein Oberbegriff für bestimmte und unbestimmte Integrale.
- Das bestimmte Integral einer Funktion f ist eine Zahl und wird bestimmt genannt, weil es das Integral einer Funktion in einem gegebenen Intervall ist. Zum Beispiel ergibt das Integral einer reellen Funktion f(x) im Intervall a ≤ x ≤ b die Fläche unter dem Funktionsgraphen von f(x) in den Intervallgrenzen a und b an. Funktionsabschnitte, bei denen f(x) < 0 ist, werden negativ in die Flächenberechnung gezählt. Dabei schreibt man
- Das unbestimmte Intervall einer Funktion f ist ihre Stammfunktion F. Die erste Ableitung von F ist f. Aufgrund der o.g. Ableitungsregeln hat eine Funktion f nicht eine einzige Stammfunktion, sondern viele. Beispielsweise sind und Stammfunktionen von , da Summanden, die nicht die Variable x enthalten, in der Ableitung wegfallen. Die Stammfunktion wird benötigt, um bestimmte Integrale einer Funktion zu berechnen. Dabei gilt , wobei die rechte Seite verkürzt notiert werden kann als
Grundbegriffe der Logik und logische Operatoren
- Proposition: eine Aussage oder ein Satz, der wahr oder falsch sein kann, aber nicht beides gleichzeitig. Damit ist die Proposition ein Grundbaustein für die Untersuchung logischer Argumente und Schlussfolgerungen. Das bedeutet, dass jede Proposition eine klare Bedeutung hat, die entweder wahr oder falsch ist, aber nicht beides zugleich. Propositionen werden oft mit Buchstaben wie p, q, r usw. symbolisiert, um in komplexeren logischen Ausdrücken verwendet zu werden.
- Wahrheitswert: ein logischer Wert, der angibt, ob eine Aussage wahr oder falsch ist, oft mit w und f oder t und f (true/false) abgekürzt. Wenn man von diesen zwei Wahrheitswerten, also wahr oder falsch ausgeht, spricht man von zweiwertiger Logik. Der Wahrheitswert einer Aussage ist abhängig vom Kontext und den zugrundeliegenden Annahmen oder Prämissen.
- Verbindung: Operator, der Aussagen miteinander verknüpft. Damit können neue Aussagen gebildet und Beziehungen zwischen Aussagen untersucht werden.
- Konjunktion: die Verknüpfung zweier Aussagen durch das logische "UND". Eine Konjunktion ist wahr, wenn beide Aussagen, die sie verknüpft, wahr sind, ansonsten ist sie falsch (false). Ihr Symbol ist ∧
- Disjunktion: die Verknüpfung zweier Aussagen durch das logische "ODER". Eine Disjunktion ist wahr, wenn mindestens eine der beiden Aussagen, die sie verknüpft, wahr ist; Sie ist nur dann falsch, wenn beide Aussagen falsch sind; ihr Symbol ist ∨
- exklusive Disjunktion: ist wahr, wenn genau eine der beiden Aussagen, die sie verknüpft, wahr ist, und falsch, wenn beide Aussagen gleichzeitig wahr oder beide gleichzeitig falsch sind. Häufig wird sie mit ⊻ symbolisiert.
- Implikation: eine logische Beziehung zwischen zwei Aussagen, bei der die Wahrheit der ersten Aussage die Wahrheit der zweiten Aussage bestimmt. Die Implikation wird oft mit "wenn..., dann..." ausgedrückt. Ihr Symbol ist →
- Äquivalenz: eine gegenseitige logische Beziehung zwischen zwei Aussagen, bei der beide Aussagen entweder gleichzeitig wahr oder gleichzeitig falsch sind. Eine Äquivalenz zwischen zwei Aussagen wird oft mit dem Begriff "wenn und nur wenn" oder "genau dann, wenn" ausgedrückt. Sie bedeutet, dass die Wahrheit der einen Aussage die Wahrheit der anderen impliziert und umgekehrt. Ihr Symbol ist ⇔
- Negation: die Verneinung einer Aussage. Sie wird verwendet, um eine Aussage in ihre entgegengesetzte Form umzuwandeln. Ihr Symbol ist ¬
- Wahrheitstabelle: Methode in der Logik, um alle möglichen Wahrheitswerte einer logischen Verbindung oder Funktion systematisch darzustellen. Sie zeigt alle Kombinationen von Wahrheitswerten für die beteiligten Aussagen und gibt den resultierenden Wahrheitswert der Verbindung an.
- Man identifiziert zuerst alle relevanten Propositionen oder Variablen und jede mögliche Kombination der Wahrheitswerte dieser Propositionen. Bei n Propositionen gibt es Kombinationen von Wahrheitswerten
- Für die einzelnen Kombinationen wird jeweils der Wahrheitswert errechnet und tabellarisch abgetragen
- Beispiel: Es gilt für die Aussagen p und q die Konjunktion p∧q, das heißt, die Konjunktion wird dann wahr, wenn p und q wahr sind. Die Wahrheitstabelle für diesen Fall könnte sein:
| p | q | p∧q |
|---|---|---|
| w | w | w |
| w | f | f |
| f | w | f |
| f | f | f |
- Gültigkeit & Korrektheit
- Die Gültigkeit eines Arguments oder einer logischen Formel sagt aus, ob die Schlussfolgerung aus den gegebenen Prämissen logisch folgt, sie ist also eine Aussage über die Struktur des Arguments. Die Schlussfolgerung eines gültigen Arguments muss wahr sein, wenn seine Prämissen wahr sind, unabhängig vom tatsächlichen Wahrheitsgehalt der Prämissen oder Schlussfolgerung.
- Die Korrektheit eines Arguments betrifft die Wahrheit der Prämissen und der Schlussfolgerung. Ein korrektes Argument ist, wenn die Prämissen wahr sind und auch die Schlussfolgerung wahr ist. Ein korrektes Argument ist also immer gültig, aber ein gültiges Argument nicht zwingend korrekt.
- Schlussregeln: methodische Vorgehensweisen, um aus gegebenen Prämissen logisch gültige Schlussfolgerungen zu ziehen
- Modus ponens (Befolgung): Wenn p wahr ist und p→q wahr ist, dann ist q wahr.
- Modus tollens (Verneinung): Wenn p→q wahr ist und q falsch ist, dann ist p falsch
- Hypothetischer Syllogismus: Wenn p→q wahr ist und q→r wahr ist, dann ist p→r wahr.
- Disjunktiver Syllogismus: Wenn p∨q wahr ist und ¬p wahr ist, dann ist q wahr.
- Einführung und Elimination von Konjunktionen:
- Einführung: Wenn p wahr ist und q wahr ist, dann ist p∧q wahr.
- Elimination: Wenn p∧q wahr ist, dann sind p und q wahr.
- Einführung und Elimination von Disjunktionen:
- Einführung: Wenn p wahr ist, dann ist p∨q wahr.
- Elimination: Wenn p∨q wahr ist und p→r wahr ist und q→r wahr ist, dann ist r wahr.
- Quantor/Quantifikator: Ausdruck, der angibt, wie viele oder welche Elemente einer Menge eine bestimmte Eigenschaft erfüllen. Die zwei grundlegensten Quantoren sind:
- Allquantor: sagt aus, dass eine bestimmte Eigenschaft für alle Elemente einer Menge gilt; Symbol: ∀
- Existenzquantor: sagt aus, dass es mindestens ein Element in einer Menge gibt, für das eine bestimmte Eigenschaft gilt; Symbol: ∃


![{\displaystyle a={\sqrt[{b}]{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90cccd6642886a8b91fcac79c94ad2feb464ff7)
![{\displaystyle 5={\sqrt[{3}]{125}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e2b59048afac185e8afebd686263a6b7a239f30)









![{\displaystyle [F(x)]_{a}^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58519abfc26ff52a5dafdccf5273cac4d77c85fa)
