Skalentypen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
''Beispiel Haarfarbe: Die Haarfarbe "braun" im empirischen Relativ erhält im numerischen Relativ eine 1, "blond" erhält 2, "rot" 3 und "schwarz" 4. Personen, die dieselbe Zahl erhalten (numerisches Relativ) haben die gleiche Haarfarbe (empirisches Relativ). Anhand der Zahlen kann ich die Personen auf ihre Unterschiedlichkeit bzw. Gleichheit untersuchen (gleiche versus andere Haarfarbe) und nachverfolgen, wie viele Personen der jeweiligen Haarfarben-Kategorie zugeordnet wurden (Häufigkeitsverteilung).''<br/> | ''Beispiel Haarfarbe: Die Haarfarbe "braun" im empirischen Relativ erhält im numerischen Relativ eine 1, "blond" erhält 2, "rot" 3 und "schwarz" 4. Personen, die dieselbe Zahl erhalten (numerisches Relativ) haben die gleiche Haarfarbe (empirisches Relativ). Anhand der Zahlen kann ich die Personen auf ihre Unterschiedlichkeit bzw. Gleichheit untersuchen (gleiche versus andere Haarfarbe) und nachverfolgen, wie viele Personen der jeweiligen Haarfarben-Kategorie zugeordnet wurden (Häufigkeitsverteilung).''<br/> | ||
<br/> | <br/> | ||
<u>Die '''Ordinalskala'''</u> | <u>Die '''Ordinalskala'''</u> <br/> | ||
Eine Ordinalskala (auch Rangskala genannt) ordnet empirischen Relativen Zahlen zu, die Rückschlüsse auf eine '''Rangreihenfolge''' der Objekte bezüglich des untersuchten Kriteriums zulassen. Das bezüglich des Kriteriums dominierende Objekt erhält eine größere Zahl. Somit kann bei ordinalskalierten Daten eine Aussage über Größer-kleiner-Relationen gemacht werden. | Eine Ordinalskala (auch Rangskala genannt) ordnet empirischen Relativen Zahlen zu, die Rückschlüsse auf eine '''Rangreihenfolge''' der Objekte bezüglich des untersuchten Kriteriums zulassen. Das bezüglich des Kriteriums dominierende Objekt erhält eine größere Zahl. Somit kann bei ordinalskalierten Daten eine Aussage über Größer-kleiner-Relationen gemacht werden. | ||
[[Datei:Ordinalskala.jpg|400px|thumb|zentriert|Ordinalskala]] | [[Datei:Ordinalskala.jpg|400px|thumb|zentriert|Ordinalskala]] | ||
| Zeile 22: | Zeile 22: | ||
Anhand der Zahlen kann festgestellt werden, wer der schnellste Läufer war, wer der zweitschnellste usw. Es kann also Gleichheit&Ungleichheit und eine Rangordnung festgestellt werden (1.Platz, 2.Platz…).'' | Anhand der Zahlen kann festgestellt werden, wer der schnellste Läufer war, wer der zweitschnellste usw. Es kann also Gleichheit&Ungleichheit und eine Rangordnung festgestellt werden (1.Platz, 2.Platz…).'' | ||
<br/> | <br/> | ||
<u>Die '''Intervallskala'''</u> <br/> | |||
Objekte werden auf einer Intervallskala numerisch so abgebildet, dass anhand der zugeordneten Zahlen verschieden große '''Differenzen''' zwischen verschiedenen Objekten ausgemacht werden können. <br/> | Objekte werden auf einer Intervallskala numerisch so abgebildet, dass anhand der zugeordneten Zahlen verschieden große '''Differenzen''' zwischen verschiedenen Objekten ausgemacht werden können. <br/> | ||
[[Datei:Intervallskala.jpg|300px|thumb|zentriert|Intervallskala]] | [[Datei:Intervallskala.jpg|300px|thumb|zentriert|Intervallskala]] | ||
| Zeile 28: | Zeile 29: | ||
''''Bei vier Personen wird der Intelligenzquotient gemessen. Person 1 erreicht eine Punktzahl von 95, Person 2 von 100, Person 3 von 105 und Person 4 eine Punktzahl von 110. Auf Intervallskalen-Niveau kann nun festgestellt werden, ob Personen unterschiedliche oder gleiche Leistungen erbracht haben, wer eine höhere oder niedrigere Leistung erbracht hat (Rangordnung) und zusätzlich, um <u>wie viele</u> Punkte Person 2 besser abgeschnitten hat als Person 1, oder, dass die Leistung von Person 2 gleichweit von der Leistung von den Personen 1 und 3 entfernt ist etc.'' | ''''Bei vier Personen wird der Intelligenzquotient gemessen. Person 1 erreicht eine Punktzahl von 95, Person 2 von 100, Person 3 von 105 und Person 4 eine Punktzahl von 110. Auf Intervallskalen-Niveau kann nun festgestellt werden, ob Personen unterschiedliche oder gleiche Leistungen erbracht haben, wer eine höhere oder niedrigere Leistung erbracht hat (Rangordnung) und zusätzlich, um <u>wie viele</u> Punkte Person 2 besser abgeschnitten hat als Person 1, oder, dass die Leistung von Person 2 gleichweit von der Leistung von den Personen 1 und 3 entfernt ist etc.'' | ||
<br/> | <br/> | ||
<u>Die '''Verhältnisskala'''</u> | <u>Die '''Verhältnisskala'''</u> <br/> | ||
Über Daten auf einer Verhältnisskala können Aussagen über '''empirische Verhältnisse''' der zugehörigen Objekte gemacht werden. Das mathematische Verhältnis zwischen zwei Zahlen entspricht dem empirischen Verhältnis der zugehörigen Objekte. Hierzu ist es nötig, dass eine Skala einen "Anfangs-" oder Referenzpunkt besitzt, also ''bei Null beginnt''.<br/> | Über Daten auf einer Verhältnisskala können Aussagen über '''empirische Verhältnisse''' der zugehörigen Objekte gemacht werden. Das mathematische Verhältnis zwischen zwei Zahlen entspricht dem empirischen Verhältnis der zugehörigen Objekte. Hierzu ist es nötig, dass eine Skala einen "Anfangs-" oder Referenzpunkt besitzt, also ''bei Null beginnt''.<br/> | ||
[[Datei:Intervallskala.jpg|300px|thumb|zentriert|Verhältnisskala]] | [[Datei:Intervallskala.jpg|300px|thumb|zentriert|Verhältnisskala]] | ||
| Zeile 34: | Zeile 35: | ||
''Die Körpergröße von vier Personen wird gemessen und die Daten auf einer Verhältnisskala abgetragen. Eine Person mit der Körpergröße von 100cm erhält das numerische Relativ 1. Einer Person mit 200cm Körpergröße das numerische Relativ 2. Anhand der Zahlen kann man feststellen, dass Person 2 doppelt so groß ist wie Person 1 (200:100 --> 2:1).'' | ''Die Körpergröße von vier Personen wird gemessen und die Daten auf einer Verhältnisskala abgetragen. Eine Person mit der Körpergröße von 100cm erhält das numerische Relativ 1. Einer Person mit 200cm Körpergröße das numerische Relativ 2. Anhand der Zahlen kann man feststellen, dass Person 2 doppelt so groß ist wie Person 1 (200:100 --> 2:1).'' | ||
<br/> | |||
<br/> | <br/> | ||
Die vier Skalentypen unterscheiden sich also in dem Informationsgrad bezüglich Verschiedenheit, Rangordnung, Differenz- und Verhältnisdarstellung. Die folgende Abbildung fasst dies zusammen: | Die vier Skalentypen unterscheiden sich also in dem Informationsgrad bezüglich Verschiedenheit, Rangordnung, Differenz- und Verhältnisdarstellung. Die folgende Abbildung fasst dies zusammen: | ||
Version vom 18. Februar 2015, 17:47 Uhr
An Skalen wird der Anspruch gestellt, dass sie ein empirisches Relativ homomorph (strukturerhaltend, siehe Messtheorie) in ein numerisches Relativ abbilden können. Das empirische Relativ ist das tatsächlich vorliegende Verhältnis zwischen den zu untersuchenden Objekten. Das numerische Relativ stellt die theoretische Abbildung dieses Verhältnisses in Zahlen dar. Skalen können sich darin unterscheiden, wieviel Information sie über das empirische Relativ beinhalten.
Man unterscheidet vier Typen von Skalen mit unterschiedlichem Informationsgehalt:
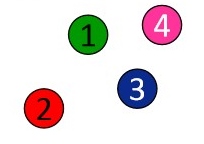
Die Nominalskala
Daten auf einer Nominalskala lassen sich lediglich auf Gleichheit oder Ungleichheit überprüfen.
Objekte mit gleicher Merkmalsausprägung bekommen die gleichen Zahlen zugeordnet, Objekte mit unterschiedlicher Merkmalsausprägung bekommen unterschiedliche Zahlen zugeordnet.
Nominalskalierte Daten können statistisch lediglich auf Häufigkeitsverteilungen untersucht werden.
Beispiel Haarfarbe: Die Haarfarbe "braun" im empirischen Relativ erhält im numerischen Relativ eine 1, "blond" erhält 2, "rot" 3 und "schwarz" 4. Personen, die dieselbe Zahl erhalten (numerisches Relativ) haben die gleiche Haarfarbe (empirisches Relativ). Anhand der Zahlen kann ich die Personen auf ihre Unterschiedlichkeit bzw. Gleichheit untersuchen (gleiche versus andere Haarfarbe) und nachverfolgen, wie viele Personen der jeweiligen Haarfarben-Kategorie zugeordnet wurden (Häufigkeitsverteilung).
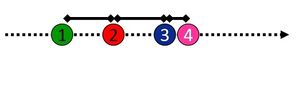
Die Ordinalskala
Eine Ordinalskala (auch Rangskala genannt) ordnet empirischen Relativen Zahlen zu, die Rückschlüsse auf eine Rangreihenfolge der Objekte bezüglich des untersuchten Kriteriums zulassen. Das bezüglich des Kriteriums dominierende Objekt erhält eine größere Zahl. Somit kann bei ordinalskalierten Daten eine Aussage über Größer-kleiner-Relationen gemacht werden.
Beispiel Sportwettkampf: Der erste Leichtathlet, der die Ziellinie überquert (empirisches Relativ) erhält im numerischen Relativ eine 1. Der Zweite die 2, usw. Sportler, die gleichzeitig die Ziellinie überqueren erhalten die gleiche Zahl.
Anhand der Zahlen kann festgestellt werden, wer der schnellste Läufer war, wer der zweitschnellste usw. Es kann also Gleichheit&Ungleichheit und eine Rangordnung festgestellt werden (1.Platz, 2.Platz…).
Die Intervallskala
Objekte werden auf einer Intervallskala numerisch so abgebildet, dass anhand der zugeordneten Zahlen verschieden große Differenzen zwischen verschiedenen Objekten ausgemacht werden können.
''Bei vier Personen wird der Intelligenzquotient gemessen. Person 1 erreicht eine Punktzahl von 95, Person 2 von 100, Person 3 von 105 und Person 4 eine Punktzahl von 110. Auf Intervallskalen-Niveau kann nun festgestellt werden, ob Personen unterschiedliche oder gleiche Leistungen erbracht haben, wer eine höhere oder niedrigere Leistung erbracht hat (Rangordnung) und zusätzlich, um wie viele Punkte Person 2 besser abgeschnitten hat als Person 1, oder, dass die Leistung von Person 2 gleichweit von der Leistung von den Personen 1 und 3 entfernt ist etc.
Die Verhältnisskala
Über Daten auf einer Verhältnisskala können Aussagen über empirische Verhältnisse der zugehörigen Objekte gemacht werden. Das mathematische Verhältnis zwischen zwei Zahlen entspricht dem empirischen Verhältnis der zugehörigen Objekte. Hierzu ist es nötig, dass eine Skala einen "Anfangs-" oder Referenzpunkt besitzt, also bei Null beginnt.
Die Körpergröße von vier Personen wird gemessen und die Daten auf einer Verhältnisskala abgetragen. Eine Person mit der Körpergröße von 100cm erhält das numerische Relativ 1. Einer Person mit 200cm Körpergröße das numerische Relativ 2. Anhand der Zahlen kann man feststellen, dass Person 2 doppelt so groß ist wie Person 1 (200:100 --> 2:1).
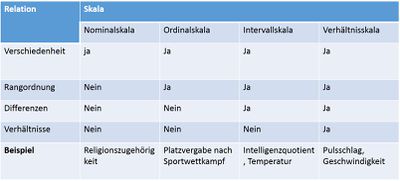
Die vier Skalentypen unterscheiden sich also in dem Informationsgrad bezüglich Verschiedenheit, Rangordnung, Differenz- und Verhältnisdarstellung. Die folgende Abbildung fasst dies zusammen:
Nach Hussy u.a., 2010