Alpha-Fehler

Der Alpha-Fehler (α-Fehler, Fehler erster Art, Annahmefehler) bezeichnet in der Statistik die Wahrscheinlichkeit, zu Unrecht die Nullhypothese (H0) abzulehnen und die Alternativhypothese (H1) anzunehmen.

Da in der Wissenschaft immer nur Stichproben getestet werden und die Verteilung der Variablen in der Grundgesamtheit nie bekannt ist, gibt es immer eine gewisse Wahrscheinlichkeit, mit der man sich bei der Verallgemeinerung von Untersuchungsergebnissen auf die Grundgesamtheit irren kann. Hier wird zwischen zwei Arten des "Irrens" unterschieden:
1. man nimmt die Alternativhypothese (H1) an, obwohl die Nullhypothese (H0) gilt (α-Fehler)
2. man nimmt die Nullhypothese (H0) an, obwohl die Alternativhypothese (H1) gilt (β-Fehler)

Der Alpha-Fehler bezeichnet also den Fall, dass aufgrund der Stichprobenergebnisse die Alternativhypothese angenommen wird, obwohl in Wirklichkeit die Nullhypothese zutrifft.

Die Wahrscheinlichkeit, dass der Alpha-Fehler eintritt (Alpha-Fehler-Wahrscheinlichkeit), wird gemeinhin Irrtumswahrscheinlichkeit genannt und in der Statistik mit Signifikanztests als p bezeichnet. Nur wenn p gering genug ist, kann ein experimentell ermitteltes Ergebnis als zufallskritisch abgesichert gelten. Das heißt, das an der Stichprobe gewonnene Ergebnis ist mit mindestens 95%-iger (wenn p≤.05) bzw. mindestens 99%-iger (wenn p≤.01) Wahrscheinlichkeit NICHT durch Zufall oder Artefakte zustande gekommen, sondern verhält sich auch in der Grundgesamtheit so wie im Experiment.

Beispiel:
In einer Untersuchung wird eine herkömmliche mit einer neuen Lehrmethode verglichen. Der Experimentalgruppe wird ein Lehrstoff mit der neuen Methode gelehrt, die Kontrollgruppe wird nach der herkömmlichen Methode unterrichtet. Es wird vermutet, dass die Experimentalgruppe einen besseren Lernerfolg (bessere Noten) erzielt als die Kontrollgruppe (H1: µEG < µKG [Schulnoten sind negativ gepolt! Je geringer die Note, umso besser ist der Schüler!]). Die Nullhypothese besagt, dass entweder kein Unterschied zwischen den Gruppen besteht oder die Experimentalgruppe schlechtere Noten erzielt als die Kontrollgruppe (H0: µEG ≥ µKG). Die Zeugnisnoten der Experimentalgruppe sind signifikant (p<.01) besser als die der Kontrollgruppe. Das bedeutet, dass die Wahrscheinlichkeit, dass dieses Ergebnis falsch ist und in Wirklichkeit (in der Grundgesamtheit) die traditionelle Lehrmethode bessere oder gleich gute Lernerfolge erzielt, bei unter 1% liegt.

Zusammenhang zwischen Alpha-Fehler und Beta-Fehler

Der Alpha-Fehler und der Beta-Fehler kommen dann zustande, wenn aufgrund der an einer Stichprobe gewonnenen Ergebnisse Annahmen getroffen werden, die sich in der Grundgesamtheit anders darstellen. Der Alpha-Fehler stellt eine falsche Annahme der Alternativhypothese (H1) dar, der Beta-Fehler ist die falsche Annahme der Nullhypothese (H0).

Die folgende Abbildung verdeutlicht die Beziehungen noch einmal grafisch:

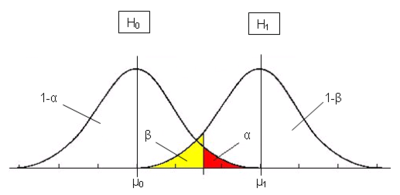
Je kleiner der α-Fehler in einer Untersuchung ist, umso seltener wird fälschlicherweise die Nullhypothese abgelehnt – allerdings steigt dann die Wahrscheinlichkeit, zu Unrecht die Nullhypothese anzunehmen und die Alternativhypothese abzulehnen (β-Fehler). Man kann jedoch aus der Größe des Alpha-Fehlers nicht direkt die Größe des Beta-Fehlers ableiten, ebenso wenig wie andersherum. Die beiden Fehlerarten werden unabhängig voneinander und mit verschiedenen Methoden bestimmt. Die Größe des Alpha-Fehlers wird durch das Signifikanzniveau kontrolliert, die Größe des Beta-Fehlers richtet sich nach der H1.