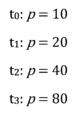Differentialgleichungsmodelle

Viele Prozesse, die modelliert werden sollen, durchlaufen eine zeitliche Entwicklung: Wenn man wie in einem Film sehr viele Einzelbilder des Prozesses nacheinander machen würde, dann könnte man sehen, wie sich der Prozess langsam Schritt für Schritt entwickelt bzw. verändert. Man könnte beim Ansehen der Bilder zu der Annahme kommen, dass jeder Schritt auf den vorherigen Schritten aufbaut, so wie wir beim Denken den Eindruck haben, dass ein Gedanke den nächsten ergibt.

Das mathematische Werkzeug um solche zeitlichen Entwicklungen von Systemen und Prozessen darzustellen sind Differentialgleichungen. Differentialgleichungen sind mathematische Gleichungen, die eine Veränderung (eine Differenz) abbilden. Mathematisch gesprochen: Sie setzen eine bestimmte Funktion mit ihrer Ableitung in Beziehung. Konkret heißt das, dass die Differentialgleichung den Zusammenhang zwischen einer bestimmten Größe zum Zeitpunkt t, und der daraus folgenden Veränderung dieser Größe beschreibt. Den aktuellen Wert bezeichnet man entsprechend mit f(t), und die Veränderung, besser gesagt die Veränderungsrate dieser Größe mit f‘(t).

Zum einfacheren Verständnis führen wir im Folgenden Differentialgleichungen anhand von Modellen aus unserer Nachbardisziplin, der Biologie, ein. Diese Modelle sind aufgrund ihres Gegenstandes etwas leichter greifbar als die psychologischen Versionen.

Nehmen wir als einfaches Beispiel das exponentielle Wachstum einer Bakterienkolonie der Größe p=10 zum Startzeitpunkt t₀. In einer (sehr künstlichen) hypothetischen Umwelt verdoppeln sich die Bakterien ohne zu sterben zu jedem Zeitschritt t:

Mathematisch könnte man die Entwicklung der Population in einer exponentiellen Formel zusammenfassen:

Wir können aber auch das Wachstum von Zeitpunkt zu Zeitpunkt beschreiben, wie wir es beobachtet haben. Dann könnten wir schreiben