Die F-Verteilung

Die F-Verteilung oder Fisher-Verteilung ist eine stetige, rechtsschiefe Wahrscheinlichkeitsverteilung, die in der Teststatistik im Rahmen unterschiedlicher F-Tests, v.a. bei Varianzvergleichen, eine wichtige Rolle spielt.

Die F-Verteilung entsteht dadurch, dass aus mehreren Grundgesamtheiten (mit den Parametern µ_i und σ_i) wiederholt Stichproben gezogen werden. Für jede dieser Stichproben wird mithilfe der folgenden Formel ein F-Wert bestimmt:

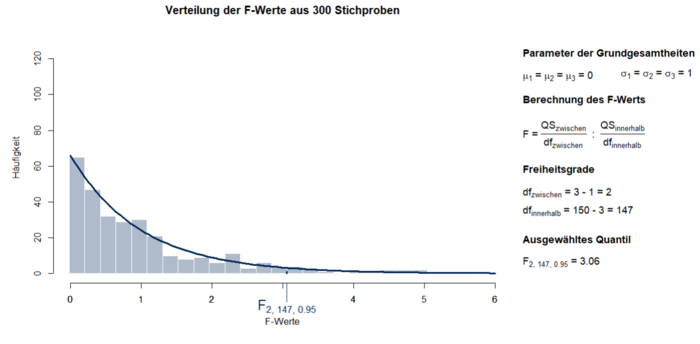
Ein F-Wert setzt die Quadratsumme zwischen den Gruppen mit der Quadratsumme innerhalb der Gruppen, jeweils relativiert an den Freiheitsgraden, ins Verhältnis. Es wird also die systematische Varianz zwischen den Gruppen mit der Fehlervarianz innerhalb der Gruppen verglichen. Die dadurch entstehenden F-Werte sind streng positiv. Ein Beispiel einer F-Verteilung aus 3 Gruppen mit einer Größe von jeweils 50 wird in Abbildung 1 dargestellt.

Die Quantile der F-Verteilung und die damit einhergehenden p-Werte beschreiben den Wert unterhalb dessen ein bestimmter Anteil der Fläche der Verteilung liegt. In Abbildung ist das 95%-Quantil der Verteilung dargestellt. Die Quantile müssen nicht separat berechnet werden, sondern lassen sich aus Tabellen ablesen oder sind direkt in den Statistikprogrammen implementiert.

kkk Im Video wird die F-Verteilung näher erläutert.

kkk Wie die F-Verteilung von der Anzahl der Gruppen und der jeweiligen Gruppengröße abhängt, lässt sich in der interaktiven Simulation nachvollziehen.

Weiterführende Literatur

Rudolf, M. & Kuhlisch, W. (2020). Biostatistik. Eine Eine Einführung für Bio- und Umweltwissenschaftler (2. Aufl.). München: Pearson Studium. (Kapitel 3.3)