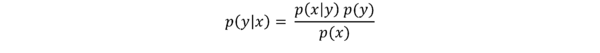Probabilistische Modelle
Kognitive Prozesse, wie zum Beispiel Wahrnehmungsurteile, beruhen auf unsicheren Schlussfolgerungen und müssen daher die Unsicherheit der Informationen berücksichtigen. Wenn man in der Dunkelheit die Umrisse einer bekannten Person erkennt, dann ist es wichtig, die Unsicherheit dieser Einschätzung im Kopf zu haben um sein Verhalten entsprechend anzupassen (und keinem ggf. gefährlichen Unbekannten unvorsichtig in die Arme zu rennen).
Im Gegensatz zu deterministischen Modellen berücksichtigen probabilistische Modelle explizit diese Unsicherheit in den Inputs und Outputs eines Verarbeitungsprozesses. Durch Quantifizierung der Unsicherheit (Zuverlässigkeit / Risiko) in den Messungen, den Modellparametern und der Passung des Modells an die Daten geben probabilistische Vorhersagen eine Reihe oder Verteilung an möglichen Outcomes vor statt einer Einzeleinschätzung. Dies wird einer komplexen und verrauschten Realität in der Regel besser gerecht. Doch wie repräsentiert man Unsicherheit?
Wahrscheinlichkeitstheoretische Grundlagen
Probabilistische Modelle sind mathematische Modelle, die Zufallsvariablen und Wahrscheinlichkeitsverteilungen miteinschließen. Zufallsvariablen stellen das potentielle Ergebnis eines unsicheren Ereignisses dar (z.B. die Augenzahl eines Würfelwurfs); sie bilden Ereignisse als Zahlen ab. Wahrscheinlichkeitsverteilungen weisen den verschiedenen potentiellen Ergebnissen Wahrscheinlichkeitswerte zu (z.B. 1/6 für jede der sechs Augenzahlen).
Wenn wir X als unsere Zufallsvariable über eine Menge von messbaren Ereignissen definieren, dann gibt uns P(X = x) die Wahrscheinlichkeit, dass X den spezifischen Wert x annimmt (kurz geschrieben: p(x)). Alle diese Wahrscheinlichkeiten sind positiv und sie summieren sich über die Ausprägungen der Zufallsvariable zu 1 auf.
Wichtige Begriffe aus der probabilistischen Theorie zum Auftreten von Merkmalskombinationen lassen sich durch eine Kontingenztafel veranschaulichen, die in ihren Zellen die Häufigkeiten nij für die Ereigniskombinationen der Zufallsvariablen X und Y enthält. Diese Ereignishäufigkeiten nij ergeben über alle Kombinationen summiert die Gesamthäufigkeit N und addieren sich an den Seiten zu den Randhäufigkeiten auf, jeweils über die Zeilen (rj) und Spalten (ci) der Kontingenztafel:
Die Verbundwahrscheinlichkeit der Ereignisse xi und yj, d.h. die Wahrscheinlichkeit ihres gleichzeitigen Eintretens ist:
Also die Häufigkeit mit der diese Ereignisse gemeinsam auftreten nij durch die Häufigkeit aller Ereigniskombinationen N.
Die Randwahrscheinlichkeit bezeichnet die Wahrscheinlichkeit für die Ausprägung einer Zufallsvariable über die Ausprägungen der anderen Zufallsvariablen hinweg, also die relative Wahrscheinlichkeit für die Ereignisse einer bestimmten Reihe oder Spalte der Kontingenztafel bzw. die jeweilige Randhäufigkeit durch die Gesamthäufigkeit N. Für eine bestimmte Reihe lautet die Formel:
Die bedingte Wahrscheinlichkeit P(Y | X) ist die Wahrscheinlichkeit des Eintretens eines Ereignisses aus Y unter der Bedingung, dass das Eintreten eines Ereignisses aus X bereits bekannt ist. Sie berechnet sich aus der Häufigkeit des Eintretens beider Ereignisse und der Randhäufigkeit des bedingenden Ereignisses:
Über die Produktregel kann man die Verbundwahrscheinlichkeit zweier Ereignisse über die bedingte Wahrscheinlichkeit und die Randwahrscheinlichkeit berechnen:
Wenn wir die Produktregel nun umstellen erhalten wir:
Diese Formel geht auf den Satz des englischen Mathematikers Thomas Bayes zurück, laut dem sich für zwei Ereignisse X und Y die Wahrscheinlichkeit von Y, unter der Bedingung, dass X eingetreten ist, durch die Wahrscheinlichkeit von X, unter der Bedingung, dass Y eingetreten ist, errechnen lässt. Der Satz von Bayes erlaubt es, Schlussfolgerungen umzukehren, d.h. ausgehend von einem bekannten Wert P(X|Y) den eigentlich interessierenden Wert P(Y|X) zu bestimmen.
Bayesianische Inferenz
Die Bayes’sche Regel ist die Basis für probabilistische Schlussfolgerung (Inferenz) und Lernen. Nehmen wir an, wir haben ein lineares (Regressions-)Modell mit den Parametern β:
Unser Ziel ist es, die β-Parameter herauszufinden, gegeben den Daten D (y- und x-Werte). Konkret wollen wir also wissen, wie wahrscheinlich ein bestimmter Wert eines β-Parameters (z.B. des Intercept β0) ist, wenn wir die Daten D vorliegen haben. Um diese Wahrscheinlichkeit zu bestimmen bzw. eine bedingte Wahrscheinlichkeitsverteilung für den β-Parameter zu erhalten, greifen wir dabei auf die obige Formel von Bayes zurück (β0 und β1 sind hier zusammengefasst, werden aber separat bestimmt):