Merkmalsselektionsverfahren

Merkmalsselektionsverfahren sind exploratorische Methoden, die im Rahmen von multiplen linearen Regressionen versuchen, mit möglichst wenigen Prädiktoren möglichst viel Varianz im Kriterium aufzuklären. In multiplen linearen Regressionen kommt es häufig vor, dass aus der vorhandenen Menge an Prädiktorvariablen eine Teilmenge nicht entscheidend zur Vorhersage des Kriteriums beiträgt. Merkmalsselektionsverfahren haben das Ziel, diese Prädiktorvariablen aus der Analyse auszuschließen, um den ökonomischen, inhaltlichen und statistischen Aufwand eines Modells zu optimieren. Dafür stehen Methoden zur Verfügung, die sukzessive Prädiktoren in die Analyse aufnehmen oder entfernen und dabei die Veränderung des multiplen Bestimmtheitsmaßes betrachten. Mit einem F-Test kann die Signifikanz dieser Veränderungen bestimmt werden.

Beim Vorwärtsverfahren wird zunächst die Variable in das Modell aufgenommen, die am höchsten mit dem Kriterium korreliert, bzw. deren Aufnahme den höchsten Anstieg des Bestimmtheitsmaßes R² zur Folge hat. Anschließend werden weiterhin schrittweise die Prädiktoren in das Modell aufgenommen, welche zusätzlich zu den bereits im Modell enthaltenden Variablen zur höchsten Veränderung von R² führen. Dies wird solange fortgesetzt, bis sich das Bestimmtheitsmaß durch die Aufnahme eines weiteren Prädiktors nicht mehr signifikant erhöht.

Das Rückwärtsverfahren beginnt mit einem Modell, in dem alle vorhandenen Prädiktoren enthalten sind. Anschließend wird zunächst der Prädiktor aus dem Modell entfernt, der zur geringsten Veränderung von R² führt. Es werden anschließend solange Prädiktoren aus dem Modell entfernt, bis das Entfernen eines weiteren Prädiktors zu einem signifikanten Rückgang von R² führen würde.

Das „schrittweise Verfahren“ ist eine Kombination aus Vorwärts- und Rückwärtsverfahren. Grundsätzlich wird ein Vorwärtsverfahren durchgeführt. Zusätzlich dazu wird vor jedem Schritt überprüft, ob die Entfernung eines bereits hinzugefügten Prädiktors zu einem nicht-signifikante Rückgang des Bestimmtheitsmaßes führen würde. Ist dies der Fall, wird der entsprechende Prädiktor entfernt und das Vorwärtsverfahren wird fortgesetzt.

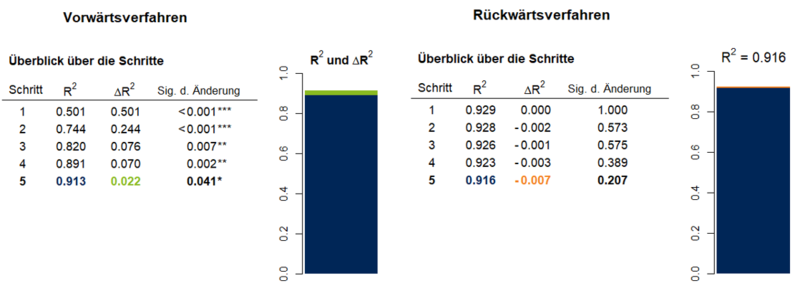
Mithilfe von Merkmalsselektionsverfahren können Hypothesen über optimale Merkmalsmengen generiert werden, die zur Bestätigung jedoch an neuen Datensätzen überprüft werden müssen. Die Ergebnisse eines solchen Verfahrens sind nicht immer eindeutig und können aufgrund von Multikollinearitätseffekten zu unterschiedlichen optimalen Merkmalsmengen führen. In Abbildung 1 werden das Vorwärts- und das Rückwärtsverfahren zur Bestimmung einer optimalen Merkmalsmenge aus 9 Prädiktoren eines fiktiven Datensatzes gegenübergestellt.

Beim Vorwärtsverfahren ergibt sich eine optimale Merkmalsmenge aus den Prädiktoren X₁, X₉, X₂, X₈ und X₄ mit einem multiplen Bestimmtheitsmaß von R² = 0.913. Beim Rückwärtsverfahren bilden die Prädiktoren X₁, X₂, X₄, X₇ und X₈ die optimale Merkmalsmenge bei einem Bestimmtheitsmaß von R² = 0.916. Vorwärts- und Rückwärtsverfahren führen hier zu einem anderen Ergebnis, es lässt sich also keine eindeutige optimale Merkmalsmenge bestimmen. Bei der Entscheidung für das passendere Modell müssen sowohl statistische als auch inhaltliche Gesichtspunkte herangezogen werden.

kkk Im Video werden die Merkmalsselektionsmethoden näher erläutert.

kkk In der interaktiven Simulation können Vorwärts-, Rückwärts- und schrittweise Verfahren mit verschiedenen Einschluss- bzw. Ausschlusskriterien grafisch nachvollzogen werden.

Weiterführende Literatur

Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.

Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.

Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.6.4). München: Pearson Studium.

Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.2.3). Göttingen: Hogrefe.