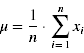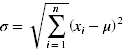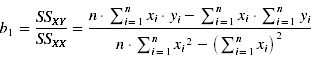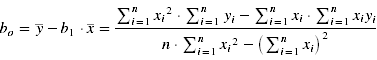Fitting & Parameter Estimation: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
:: [[Datei:Verteilungsmodelle_3_1.png|link=Ausgelagerte_Formeln#Mittelwert μ]] , [[Datei:Verteilungsmodelle_3_2.png]] | :: [[Datei:Verteilungsmodelle_3_1.png|link=Ausgelagerte_Formeln#Mittelwert μ|Ausgelagerte Formel Mittelwert]] , [[Datei:Verteilungsmodelle_3_2.png|link=Ausgelagerte_Formeln#Standardabweichung σ|Ausgelagerte Formel Standardabweichung]] | ||
| Zeile 27: | Zeile 27: | ||
:: [[Datei:Fitting_Parameter_Estimation_3.png]] | :: [[Datei:Fitting_Parameter_Estimation_3.png|link=Ausgelagerte_Formeln#Berechnung Modellparameter b1|Ausgelagerte Formel b1]] | ||
:: [[Datei:Fitting_Parameter_Estimation_4.png]] | :: [[Datei:Fitting_Parameter_Estimation_4.png|link=Ausgelagerte_Formeln#Berechnung Modellparameter b0|Ausgelagerte Formel b0]] | ||
| Zeile 37: | Zeile 37: | ||
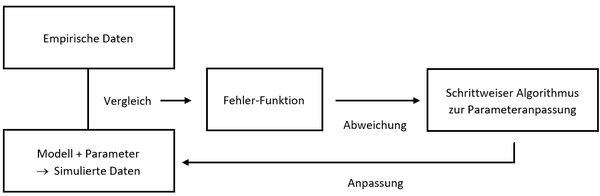
Der Prozess des Fittings verläuft dabei nach dem folgenden Schema: | Der Prozess des Fittings verläuft dabei nach dem folgenden Schema: | ||
[[Datei:Fitting_Parameter_Estimation_5.png|600px]] | [[Datei:Fitting_Parameter_Estimation_5.png|600px|link=Ausgelagerte_Bildbeschreibungen#Fitting_Parameter_Estimation|Ausgelagerte Bildbeschreibung von Fitting Parameter Estimation]] | ||
Aktuelle Version vom 10. Dezember 2021, 00:20 Uhr
Die Begriffe „Fitting“ oder „Parameter Estimation“ beschreiben den Prozess der Verwendung eines Beispieldatensatzes zur Schätzung der Parameterwerte eines Modells, um diese bestmöglich an den Datensatz anzupassen.
Handelt es sich um ein einfaches statistisches Modell wie beispielsweise das Modell der linearen Regressionsanalyse, ist es möglich, die Parameter mithilfe entsprechender Formeln direkt aus den vorliegenden Daten zu berechnen.
- Beispiel einfache lineare Regressionsanalyse
- Das ist das einfache lineare Regressionsmodell. Es ermöglicht die Art des linearen Zusammenhangs zwischen einer Prädiktorvariable und einer Kriteriumsvariable zu beschreiben. Dazu wird eine Regressionsgleichung ermittelt, welche die Vorhersage des Wertes einer Kriteriumsvariable Y aus dem Wert einer Prädiktorvariable X erlaubt.
- Der Wert der Kriteriumsvariable eines Probanden i wird dabei mittels folgender Formel berechnet:
- Möchte man nun die Parameterwerte bo und b1 bestimmen, um das Modell bestmöglich an den Datensatz anzupassen, ist dies mithilfe von entsprechenden Formeln direkt aus den Daten möglich. Dazu ist es zunächst einmal notwendig Mittelwert μ und Standardabweichung σ der Daten zu ermitteln:
- Diese Werte können im folgenden Schritt in die Formeln zur Berechnung der Modellparameter b1 und bo eingesetzt werden:
Es besteht keine Möglichkeit die Parameter komplexerer Modelle auf diese Weise zu ermitteln, da sie nicht analytisch errechenbar sind und somit eine iterative Lösung erfordern. Das heißt, die Modellparameter müssen schrittweise an die gegebenen Daten angepasst werden, bis das Modell die Daten mit so wenig Abweichungen wie möglich beschreibt und man infolgedessen den maximalen Fit erreicht hat.
Der Prozess des Fittings verläuft dabei nach dem folgenden Schema:
Die durch das Modell unter einer bestimmten Parameterwerteinstellung simulierten Daten werden mit den gegebenen empirischen Ergebnissen durch eine Fehlerfunktion (= Objective Function) verglichen, welche berechnet, wie stark das Modell von den Daten abweicht und dies in Form eines Fit-Wertes ausgibt. Mithilfe eines Algorithmus ist es möglich, die Parameter schrittweise zu verändern, um das Modell besser an den gegebenen Datensatz anzupassen. Im Anschluss jeder Parameteranpassung werden die simulierten Daten erneut durch die Fehlerfunktion mit den gegebenen Werten verglichen, bis der bestmögliche Fit erreicht wird und die Parameterschätzung somit abgeschlossen ist.
kkk Der Prozess des Fittings wird in der R-Shiny-App "Fitting" anschaulich dargestellt.