Simplex: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) (→Ablauf des Algorithmus: Ersetzung des schlechtesten Punktes 3 link einfügen pb) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
# '''Wahl der Ausgangspunkte''' <br /> Es werden drei Punkte bestimmt, die den Simplex bilden sollen. Für diese Punkte wird jeweils der Funktionswert berechnet. | # '''Wahl der Ausgangspunkte''' <br /> Es werden drei Punkte bestimmt, die den Simplex bilden sollen. Für diese Punkte wird jeweils der Funktionswert berechnet. | ||
# '''Bestimmung des schlechtesten Punktes''' <br /> Die drei Punkte werden nach Funktionswerten sortiert. Dabei ist x0 der beste Punkt, x1 der zweitbeste und x2 der schlechteste. | # '''Bestimmung des schlechtesten Punktes''' <br /> Die drei Punkte werden nach Funktionswerten sortiert. Dabei ist x0 der beste Punkt, x1 der zweitbeste und x2 der schlechteste. | ||
# '''Reflexion des schlechtesten Punktes''' <br /> Aus den beiden besseren Punkten wird der Mittelpunkt xp gebildet, an dem der schlechteste Punkt x2 reflektiert wird. Dadurch entsteht ein neuer Punkt xr. [[Datei:Reflexion.png]] | # '''Reflexion des schlechtesten Punktes''' <br /> Aus den beiden besseren Punkten wird der Mittelpunkt xp gebildet, an dem der schlechteste Punkt x2 reflektiert wird. Dadurch entsteht ein neuer Punkt xr. [[Datei:Reflexion.png|link=Ausgelagerte_Bildbeschreibungen#Reflexion|Ausgelagerte Bildbeschreibung von Reflexion]] | ||
# '''Ersetzung des schlechtesten Punktes x2''' <br /> Wenn der reflektierte Punkt xr besser ist, als das bisherige Minimum x0, wird ein sogenannter expandierter Punkt xe berechnet. Dieser Punkt entsteht dadurch, dass eine Stelle in Reflexionsrichtung gewählt wird, die noch weiter weg von den anderen Punkten liegt als der reflektierte Punkt xr. Da der reflektierte Punkt besser war als das bisherige Minimum, verspricht diese Richtung eine weitere Verbesserung. [[Datei:Expansion.png]] <br /> Aus xr und xe wird der Punkt mit dem kleinsten Funktionswert herausgesucht. Dieser Punkt ersetzt dann den bisher schlechtesten Punkt x2. Der Algorithmus beginnt dann an dieser Stelle wieder bei Schritt 2. <br /> Andernfalls wird der sogenannte kontrahierte Punkt xk ermittelt. Der Berechnung liegt entweder der reflektierte Punkt xr oder der schlechteste Ausgangspunkt x2 zu Grunde, je nachdem, welcher der beiden der bessere ist. <br />[[Datei:Kontraktion.png]] <br /> Wenn xk besser ist als der schlechteste Punkt x2, wird es der neue schlechteste Punkt und der Algorithmus kehrt zurück zu Schritt 2. Wenn xk schlechter ist als der bisher schlechteste Punkt, wird es verworfen und der Simplex wird komprimiert, das heißt, alle Punkte rücken etwas näher an das bisherige Minimum. <br />[[Datei:Komprimierung.png]] <br /> Dann geht es weiter mit Schritt 2, bis irgendwann das Minimum gefunden wurde. | # '''Ersetzung des schlechtesten Punktes x2''' <br /> Wenn der reflektierte Punkt xr besser ist, als das bisherige Minimum x0, wird ein sogenannter expandierter Punkt xe berechnet. Dieser Punkt entsteht dadurch, dass eine Stelle in Reflexionsrichtung gewählt wird, die noch weiter weg von den anderen Punkten liegt als der reflektierte Punkt xr. Da der reflektierte Punkt besser war als das bisherige Minimum, verspricht diese Richtung eine weitere Verbesserung. [[Datei:Expansion.png|link=Ausgelagerte_Bildbeschreibungen#Ersetzung_des_schlechtesten_Punktes_1|Ausgelagerte Bildbeschreibung von Ersetzung des schlechtesten Punktes 1]] <br /> Aus xr und xe wird der Punkt mit dem kleinsten Funktionswert herausgesucht. Dieser Punkt ersetzt dann den bisher schlechtesten Punkt x2. Der Algorithmus beginnt dann an dieser Stelle wieder bei Schritt 2. <br /> Andernfalls wird der sogenannte kontrahierte Punkt xk ermittelt. Der Berechnung liegt entweder der reflektierte Punkt xr oder der schlechteste Ausgangspunkt x2 zu Grunde, je nachdem, welcher der beiden der bessere ist. <br />[[Datei:Kontraktion.png|link=Ausgelagerte_Bildbeschreibungen#Ersetzung_des_schlechtesten_Punktes_2|Ausgelagerte Bildbeschreibung von Ersetzung des schlechtesten Punktes 2]] <br /> Wenn xk besser ist als der schlechteste Punkt x2, wird es der neue schlechteste Punkt und der Algorithmus kehrt zurück zu Schritt 2. Wenn xk schlechter ist als der bisher schlechteste Punkt, wird es verworfen und der Simplex wird komprimiert, das heißt, alle Punkte rücken etwas näher an das bisherige Minimum. <br />[[Datei:Komprimierung.png|link=Ausgelagerte_Bildbeschreibungen#Ersetzung_des_schlechtesten_Punktes_3|Ausgelagerte Bildbeschreibung von Ersetzung des schlechtesten Punktes 3]] <br /> Dann geht es weiter mit Schritt 2, bis irgendwann das Minimum gefunden wurde. | ||
== Vor- und Nachteile des Simplexverfahrens == | == Vor- und Nachteile des Simplexverfahrens == | ||
Der Simplexalgorithmus ist ein ableitungsfreies [[Algorithmen|Optimierungsverfahren]] und kann deshalb dort eingesetzt werden, wo Ableitungen nicht oder nur mit hohem Aufwand berechnet werden können. Das Verfahren ist relativ robust. Das Finden des globalen Minimums ist allerdings nicht garantiert. Von Nachteil ist außerdem, dass in jedem Schritt mehrere Punkte der [[Fehleroberfläche, lokale und globale Minima|Fehlerfunktion]] gleichzeitig evaluiert werden müssen, sodass der Rechenaufwand gegenüber Verfahren, die jeweils nur einen Punkt untersuchen, steigt. | Der Simplexalgorithmus ist ein ableitungsfreies [[Algorithmen|Optimierungsverfahren]] und kann deshalb dort eingesetzt werden, wo Ableitungen nicht oder nur mit hohem Aufwand berechnet werden können. Das Verfahren ist relativ robust. Das Finden des globalen Minimums ist allerdings nicht garantiert. Von Nachteil ist außerdem, dass in jedem Schritt mehrere Punkte der [[Fehleroberfläche, lokale und globale Minima|Fehlerfunktion]] gleichzeitig evaluiert werden müssen, sodass der Rechenaufwand gegenüber Verfahren, die jeweils nur einen Punkt untersuchen, steigt. | ||
Aktuelle Version vom 8. Januar 2022, 09:39 Uhr
Intuition des Simplexverfahrens
Der Simplex-Algorithmus dient dem Finden der Minima von Funktionen. Die Grundidee ist dabei, dass mehrere Punkte der Fehlerfunktion gleichzeitig evaluiert werden und anschließend immer der schlechteste Punkt durch einen neuen Punkt ersetzt wird, sodass der Algorithmus sich schrittweise dem Minimum nähert und um dieses konvergiert. Diese Punkte bilden einen Simplex, also die einfachste Form, die sich mit vorgegebenen Punkten im Parameterraum aufspannen lässt. In einem zweidimensionalen Parameterraum (also bei einem Modell mit 2 Parametern) wäre dies zum Beispiel ein Dreieck, in einem dreidimensionalen Raum eine dreiseitige Pyramide. Wir betrachten im Folgenden das Simplexverfahren nach Nelder und Mead, bei dem mit Dreiecken gearbeitet wird.
Ablauf des Algorithmus
- Wahl der Ausgangspunkte
Es werden drei Punkte bestimmt, die den Simplex bilden sollen. Für diese Punkte wird jeweils der Funktionswert berechnet. - Bestimmung des schlechtesten Punktes
Die drei Punkte werden nach Funktionswerten sortiert. Dabei ist x0 der beste Punkt, x1 der zweitbeste und x2 der schlechteste. - Reflexion des schlechtesten Punktes
Aus den beiden besseren Punkten wird der Mittelpunkt xp gebildet, an dem der schlechteste Punkt x2 reflektiert wird. Dadurch entsteht ein neuer Punkt xr.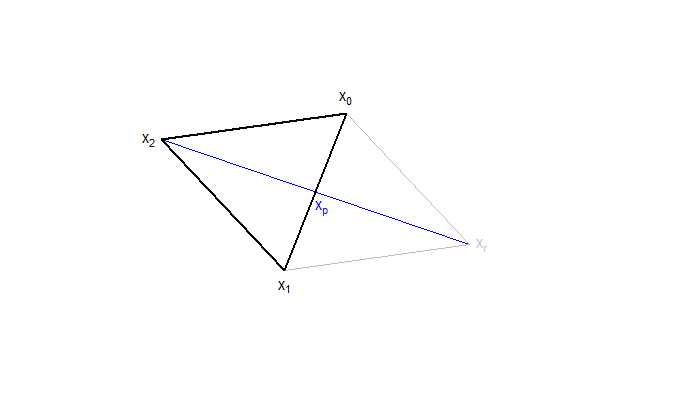
- Ersetzung des schlechtesten Punktes x2
Wenn der reflektierte Punkt xr besser ist, als das bisherige Minimum x0, wird ein sogenannter expandierter Punkt xe berechnet. Dieser Punkt entsteht dadurch, dass eine Stelle in Reflexionsrichtung gewählt wird, die noch weiter weg von den anderen Punkten liegt als der reflektierte Punkt xr. Da der reflektierte Punkt besser war als das bisherige Minimum, verspricht diese Richtung eine weitere Verbesserung.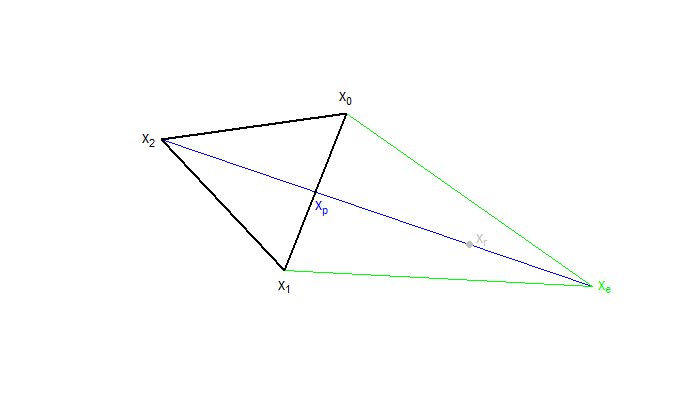
Aus xr und xe wird der Punkt mit dem kleinsten Funktionswert herausgesucht. Dieser Punkt ersetzt dann den bisher schlechtesten Punkt x2. Der Algorithmus beginnt dann an dieser Stelle wieder bei Schritt 2.
Andernfalls wird der sogenannte kontrahierte Punkt xk ermittelt. Der Berechnung liegt entweder der reflektierte Punkt xr oder der schlechteste Ausgangspunkt x2 zu Grunde, je nachdem, welcher der beiden der bessere ist.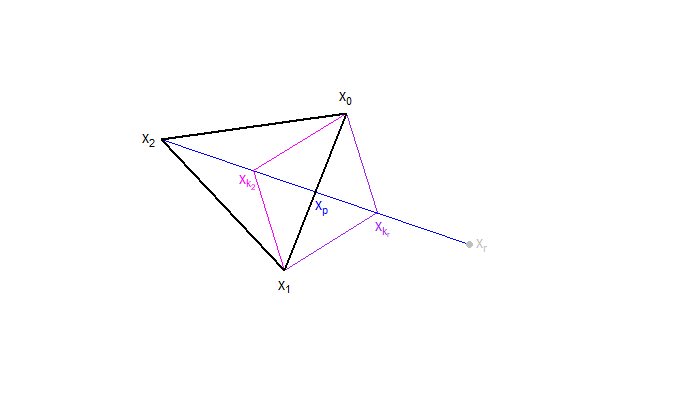
Wenn xk besser ist als der schlechteste Punkt x2, wird es der neue schlechteste Punkt und der Algorithmus kehrt zurück zu Schritt 2. Wenn xk schlechter ist als der bisher schlechteste Punkt, wird es verworfen und der Simplex wird komprimiert, das heißt, alle Punkte rücken etwas näher an das bisherige Minimum.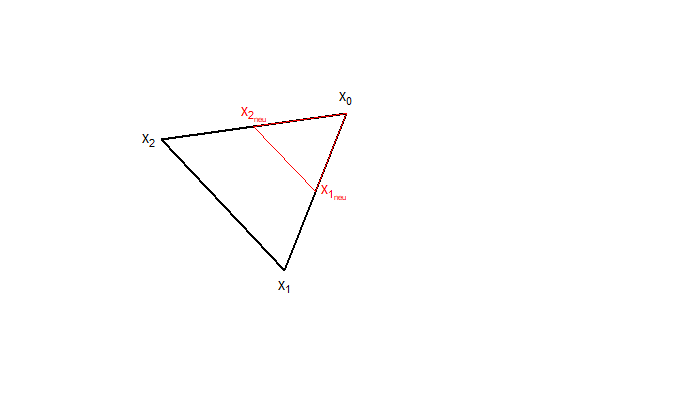
Dann geht es weiter mit Schritt 2, bis irgendwann das Minimum gefunden wurde.
Vor- und Nachteile des Simplexverfahrens
Der Simplexalgorithmus ist ein ableitungsfreies Optimierungsverfahren und kann deshalb dort eingesetzt werden, wo Ableitungen nicht oder nur mit hohem Aufwand berechnet werden können. Das Verfahren ist relativ robust. Das Finden des globalen Minimums ist allerdings nicht garantiert. Von Nachteil ist außerdem, dass in jedem Schritt mehrere Punkte der Fehlerfunktion gleichzeitig evaluiert werden müssen, sodass der Rechenaufwand gegenüber Verfahren, die jeweils nur einen Punkt untersuchen, steigt.