SSE: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Wehner (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} Artikelinhalt“) |
Paul (Diskussion | Beiträge) (SSE link einfügen pb) |
||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Kognitive Modellierung|Hauptseite}} | {{Nav|Navigation|Fitting & Parameter Estimation|Kognitive Modellierung|Hauptseite}} | ||
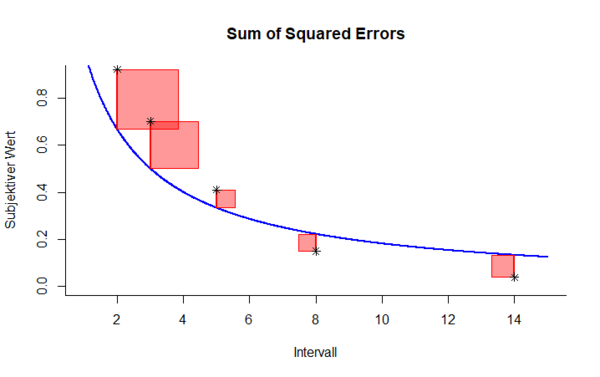
Die Abkürzung SSE bezeichnet die Fehlerquadratsumme, welche im Englischen Sum of Squared Errors genannt wird. Zur Berechnung dieses [[Abweichungsmaße]]s wird für jeden empirischen Datenpunkt die Differenz vom entsprechenden Modellwert ermittelt. Durch Quadrieren und anschließendes Aufsummieren der Werte ergibt sich schließlich die Fehlerquadratsumme. | |||
[[Datei:plot_sse.png|600px|link=Ausgelagerte_Bildbeschreibungen#SSE|Ausgelagerte Bildbeschreibung von SSE]] | |||
Wenn ''Y<sub>d</sub>'' die empirischen Y-Werte und ''Y<sub>m</sub>'' die Y-Werte des Modells sind, wird das Vorgehen durch folgende Formel beschrieben: | |||
[[Datei:Sse.png|150px|link=Ausgelagerte_Formeln#SSE|Ausgelagerte Formel Sum of Squared Errors]] | |||
Die Fehlerquadratsumme ist eines der häufigsten [[Abweichungsmaße]], da sie maßgebliche Vorteile mit sich bringt: | |||
* Durch das Quadrieren der Abweichungen werden große Fehler stärker bestraft als kleinere, sodass erstere mehr Gewicht bei der [[Fitting & Parameter Estimation|Optimierung]] bekommen. | |||
* Ein gegenseitiger Ausgleich positiver und negativer Abweichungen wird verhindert. | |||
* Nicht zuletzt wird die Fehlerquadratsumme verwendet, weil sie unkompliziert zu implementieren und leicht zu interpretieren ist. | |||
Nachteile und Grenzen der Methode: | |||
* Ein Problem stellen Ausreißer in den Daten dar, welche das [[Abweichungsmaße|Abweichungsmaß]] stark verzerren können und dadurch zu einer scheinbar schlechten Passung des Modells führen. | |||
* Zudem wird jede Differenz zwischen empirischen und entsprechenden Modelldaten gleichwertig in die Berechnung der SSE einbezogen. Dies kann ein Nachteil sein, wenn die Streuung der y-Werte sich für verschiedene x-Werte systematisch unterscheidet (das heißt, wenn Heteroskedastizität vorliegt). Ebenso ist die gleiche Gewichtung unvorteilhaft, wenn ein Teil der Daten für relevanter erachtet wird als ein anderer. Beispielhaft könnte man es für wichtiger halten, dass das Modell den subjektiven Wert über kurze Intervalle gut beschreiben kann. In diesem sowie im vorherigen Fall ist die Verwendung der gewichteten Fehlerquadratsumme eine Lösungsmöglichkeit, bei welcher jeder Abweichung ein eigenes Gewicht zugewiesen werden kann. | |||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/Fitting/fitting/ | |||
|120px]] <span style="color: white"> kkk </span> Die Entstehung der Fehleroberfläche aus der Fehlerquadratsumme wird in der R-Shiny-App [http://141.76.19.82:3838/mediawiki/Fitting/fitting/ "Fitting"] veranschaulicht. | |||
Aktuelle Version vom 18. Januar 2022, 12:47 Uhr
Die Abkürzung SSE bezeichnet die Fehlerquadratsumme, welche im Englischen Sum of Squared Errors genannt wird. Zur Berechnung dieses Abweichungsmaßes wird für jeden empirischen Datenpunkt die Differenz vom entsprechenden Modellwert ermittelt. Durch Quadrieren und anschließendes Aufsummieren der Werte ergibt sich schließlich die Fehlerquadratsumme.
Wenn Yd die empirischen Y-Werte und Ym die Y-Werte des Modells sind, wird das Vorgehen durch folgende Formel beschrieben:
Die Fehlerquadratsumme ist eines der häufigsten Abweichungsmaße, da sie maßgebliche Vorteile mit sich bringt:
- Durch das Quadrieren der Abweichungen werden große Fehler stärker bestraft als kleinere, sodass erstere mehr Gewicht bei der Optimierung bekommen.
- Ein gegenseitiger Ausgleich positiver und negativer Abweichungen wird verhindert.
- Nicht zuletzt wird die Fehlerquadratsumme verwendet, weil sie unkompliziert zu implementieren und leicht zu interpretieren ist.
Nachteile und Grenzen der Methode:
- Ein Problem stellen Ausreißer in den Daten dar, welche das Abweichungsmaß stark verzerren können und dadurch zu einer scheinbar schlechten Passung des Modells führen.
- Zudem wird jede Differenz zwischen empirischen und entsprechenden Modelldaten gleichwertig in die Berechnung der SSE einbezogen. Dies kann ein Nachteil sein, wenn die Streuung der y-Werte sich für verschiedene x-Werte systematisch unterscheidet (das heißt, wenn Heteroskedastizität vorliegt). Ebenso ist die gleiche Gewichtung unvorteilhaft, wenn ein Teil der Daten für relevanter erachtet wird als ein anderer. Beispielhaft könnte man es für wichtiger halten, dass das Modell den subjektiven Wert über kurze Intervalle gut beschreiben kann. In diesem sowie im vorherigen Fall ist die Verwendung der gewichteten Fehlerquadratsumme eine Lösungsmöglichkeit, bei welcher jeder Abweichung ein eigenes Gewicht zugewiesen werden kann.
kkk Die Entstehung der Fehleroberfläche aus der Fehlerquadratsumme wird in der R-Shiny-App "Fitting" veranschaulicht.