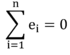Einfache lineare Regression bei metrischem Prädiktor: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) (Goldfeld-Quandt-Test link einfügen pb) |
||
| (29 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Statistik_MV|Hauptseite}} | {{Nav|Navigation|Statistik_MV|Hauptseite}} | ||
Die einfache lineare Regression ist eine statistische Methode zur Vorhersage der Messwerte einer Variablen aus den Werten einer anderen Variablen. | Die einfache lineare Regression ist eine statistische Methode zur Vorhersage der Messwerte einer Variablen aus den Werten einer anderen Variablen. Anders als die [[Einfache lineare Korrelation|Korrelationsanalyse]] ermöglicht die lineare Regression gerichtete Aussagen über den Einfluss einer Prädiktorvariable auf die Kriteriumsvariable. Dafür müssen a priori plausibel begründete Hypothesen darüber aufgestellt werden, welche Variable vorhersagt (Prädiktor) und welche vorhergesagt wird (Kriterium). Das Modell der einfachen linearen Regression lässt sich mithilfe der folgenden Formel darstellen: | ||
[[File:3_1_ELR_Formel_1.PNG| | [[File:3_1_ELR_Formel_1.PNG|145px|link=Ausgelagerte_Formeln#Einfache lineare Regression|Ausgelagerte Formel Einfache lineare Regression]] | ||
Diese beinhaltet den Wert des Kriteriums (y<sub>i</sub>) und den Wert des Prädiktors (x<sub>i</sub>) für die Untersuchungseinheit i. Die zwei Regressionskoeffizienten in der Formel sind die Regressionskonstante (b<sub>0</sub>) und der Anstieg der Regressionsgeraden b<sub>1</sub>. Die Konstante entspricht dem Schätzwert ŷ für x = 0 und damit dem Schnittpunkt der Regressionsgeraden mit der y-Achse. Der Anstieg der Regressionsgeraden beschreibt, um wie viel der ŷ -Wert ansteigt, wenn der x-Wert um eine Einheit erhöht wird. Der zufällige Fehler bzw. das Residuum e<sub>i</sub> entspricht der Abweichung des Messwertes der Kriteriumsvariable vom vorhergesagten Schätzwert (y<sub>i</sub> - ŷ<sub>i</sub>) oder grafisch veranschaulicht dem Abstand eines Messwertes von der Regressionsgerade. Bei perfekter Vorhersage durch das Modell gäbe es keine Residuen – alle Messwerte würden auf der Regressionsgerade liegen. Dieser Fall tritt in der Realität nicht ein. | Diese beinhaltet den Wert des Kriteriums (y<sub>i</sub>) und den Wert des Prädiktors (x<sub>i</sub>) für die Untersuchungseinheit i. Die zwei Regressionskoeffizienten in der Formel sind die Regressionskonstante (b<sub>0</sub>) und der Anstieg der Regressionsgeraden b<sub>1</sub>. Die Konstante entspricht dem Schätzwert ŷ für x = 0 und damit dem Schnittpunkt der Regressionsgeraden mit der y-Achse. Der Anstieg der Regressionsgeraden beschreibt, um wie viel der ŷ -Wert ansteigt, wenn der x-Wert um eine Einheit erhöht wird. Der zufällige Fehler bzw. das Residuum e<sub>i</sub> entspricht der Abweichung des Messwertes der Kriteriumsvariable vom vorhergesagten Schätzwert (y<sub>i</sub> - ŷ<sub>i</sub>) oder grafisch veranschaulicht dem Abstand eines Messwertes von der Regressionsgerade. Bei perfekter Vorhersage durch das Modell gäbe es keine Residuen – alle Messwerte würden auf der Regressionsgerade liegen. Dieser Fall tritt in der Realität nicht ein. | ||
| Zeile 11: | Zeile 11: | ||
Das Ziel der linearen Regression ist es, aus vorliegenden Daten ein Modell zu schätzen, welches eine optimale Vorhersage des Kriteriums aus dem Prädiktor ermöglicht. Dafür werden mit der Methode der kleinsten Quadrate diejenigen Regressionskoeffizienten geschätzt, mit denen die Summe der quadrierten Residuen minimal wird. Durch das Quadrieren der Residuen wird verhindert, dass sich positive und negative Residuen zu Null addieren. Außerdem werden Extremwerte bzw. stärker abweichende Residuen dadurch stärker berücksichtigt. Letzteres kann dazu führen, dass Ausreißer das Ergebnis der Regression stark beeinflussen. In solchen Fällen ist eine Ausreißerkorrektur, z.B. in Form einer robusten Regression, angemessen. Die robuste Regression ist resistent gegenüber Ausreißern und verwendet die Least Trimmed Squares Methode. Bei dieser Methode werden die Regressionsresiduen der Größe nach sortiert und nur die k Punkte mit den kleinsten Residuen werden von den ursprünglichen ''n'' Punkten in die Regressionsberechnung einbezogen. Dabei berechnet sich die Anzahl k mithilfe der folgenden Formel: | Das Ziel der linearen Regression ist es, aus vorliegenden Daten ein Modell zu schätzen, welches eine optimale Vorhersage des Kriteriums aus dem Prädiktor ermöglicht. Dafür werden mit der Methode der kleinsten Quadrate diejenigen Regressionskoeffizienten geschätzt, mit denen die Summe der quadrierten Residuen minimal wird. Durch das Quadrieren der Residuen wird verhindert, dass sich positive und negative Residuen zu Null addieren. Außerdem werden Extremwerte bzw. stärker abweichende Residuen dadurch stärker berücksichtigt. Letzteres kann dazu führen, dass Ausreißer das Ergebnis der Regression stark beeinflussen. In solchen Fällen ist eine Ausreißerkorrektur, z.B. in Form einer robusten Regression, angemessen. Die robuste Regression ist resistent gegenüber Ausreißern und verwendet die Least Trimmed Squares Methode. Bei dieser Methode werden die Regressionsresiduen der Größe nach sortiert und nur die k Punkte mit den kleinsten Residuen werden von den ursprünglichen ''n'' Punkten in die Regressionsberechnung einbezogen. Dabei berechnet sich die Anzahl k mithilfe der folgenden Formel: | ||
Mit ''p'' wird die Anzahl der zu schätzenden Koeffizienten bezeichnet, im gegebenen Fall 2 (b<sub>0</sub> und b<sub>1</sub>). | [[File:3_1_ELR_Formel_2.PNG|90px|link=Ausgelagerte_Formeln#Anzahl k (Trimmed Squares Methode)|Ausgelagerte Formel Anzahl k (Trimmed Squares Methode)]] | ||
Mit ''p'' wird die Anzahl der zu schätzenden Koeffizienten bezeichnet, im gegebenen Fall 2 (b<sub>0</sub> und b<sub>1</sub>). Im Fall der einfachen linearen Regression kann die Methode der kleinsten Quadrate so vereinfacht werden, dass die Regressionskoeffizienten mithilfe weniger Parameter bestimmbar sind. Die Steigung der Gerade lässt sich als Quotient aus der Kovarianz von Prädiktor und Kriterium und der Varianz des Prädiktors berechnen. Anschließend kann der Schätzwert der Regressionskonstante bestimmt werden: | |||
[[File:3_1_ELR_Formel_3.PNG| | [[File:3_1_ELR_Formel_3.PNG|60px|link=Ausgelagerte_Formeln#Regressionskoeffizient|Ausgelagerte Formel Regressionskoeffizient]]<span style="color: white"> kkk </span>;<span style="color: white"> kkk </span>[[File:3_1_ELR_Formel_4.PNG|100px|link=Ausgelagerte_Formeln#Regressionskonstante|Ausgelagerte Formel Regressionskonstante]] | ||
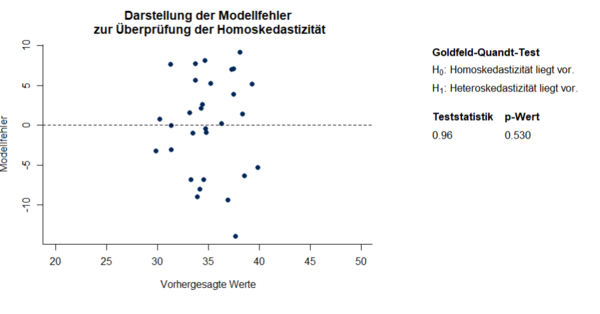
[[ | Um eine lineare Regression durchführen zu können, müssen einige Voraussetzungen erfüllt werden. Zum einen muss das lineare Modell gültig sein, d.h. zwischen Prädiktor und Kriterium muss ein linearer Zusammenhang bestehen. Eine weitere Voraussetzung ist die statistische Unabhängigkeit der Modellfehler. Diese Annahme ist gewährleistet, wenn es sich um eine Zufallsziehung von Untersuchungseinheiten (z.B. Versuchspersonen) aus der Population handelt. Bei Untereinheiten innerhalb der Population oder Abhängigkeiten von zeitlichen Faktoren kann nicht von statistischer Unabhängigkeit ausgegangen werden und es müssen andere Methoden wie z.B. die [[Hierarchische Regression]] angewendet werden. Die Zufallsvariable Modellfehler hat einen Erwartungswert von Null. Entsprechend ergibt sich für die Summe der Residuen der Wert 0: | ||
[[File:3_1_ELR_Formel_5.PNG|70px|link=Ausgelagerte_Formeln#Summe der Residuen|Ausgelagerte Formel Summe der Residuen]] | |||
Für zuverlässige Schätzungen muss der Modellfehler normalverteilt um diesen Erwartungswert streuen. Die Normalverteilung (NV) des Modellfehlers kann mithilfe entsprechender Tests, wie des Shapiro-Wilk-Tests oder anhand grafischer Veranschaulichung durch QQ-Plots überprüft werden. Im QQ-Plot werden die empirischen Quantile der erfassten Variablen den theoretischen Quantilen der NV gegenübergestellt. Bei NV befinden sich die Punkte auf einer Geraden. Eine weitere Voraussetzung ist, dass die Varianzen der Modellfehler σ² unabhängig vom Prädiktorwert x<sub>i</sub> sind, d.h. dass die Streuung der Messwerte des Kriteriums für alle Wertebereiche des Prädiktors gleich ist. Diese Voraussetzung wird als Homoskedastizität bezeichnet und lässt sich ebenfalls mit statistischen Tests (z.B. Goldfeld-Quandt Test) oder grafisch überprüfen. Grafisch bietet es sich an, die vorhergesagten Werte den Residuen gegenüberzustellen. Eine Verletzung der Homoskedastizität verursacht ineffiziente Varianzschätzungen. Ineffiziente Varianzschätzungen führen zu verzerrten Standardfehlern und in Folge dessen zu ungenauen Teststatistiken und Signifikanzschätzungen. In diesem Fall wird eine Regression mit robusten Standardfehlern empfohlen. Robuste Standardfehler korrigieren für Heteroskedastizität, indem der Standardfehler für jeden Datenpunkt einzeln auf Grundlage seines Residuums geschätzt wird. Es kann z.B. eine Variante des White-Schätzers herangezogen werden. Die Korrektur des Standardfehlers führt ebenfalls zu einer Korrektur von t- und p-Wert. Näheres zur Überprüfung der Homoskedastizität und weitere Korrekturverfahren werden in Hayes & Cai (2007) dargestellt. | Für zuverlässige Schätzungen muss der Modellfehler normalverteilt um diesen Erwartungswert streuen. Die Normalverteilung (NV) des Modellfehlers kann mithilfe entsprechender Tests, wie des Shapiro-Wilk-Tests oder anhand grafischer Veranschaulichung durch QQ-Plots überprüft werden. Im QQ-Plot werden die empirischen Quantile der erfassten Variablen den theoretischen Quantilen der NV gegenübergestellt. Bei NV befinden sich die Punkte auf einer Geraden. Eine weitere Voraussetzung ist, dass die Varianzen der Modellfehler σ² unabhängig vom Prädiktorwert x<sub>i</sub> sind, d.h. dass die Streuung der Messwerte des Kriteriums für alle Wertebereiche des Prädiktors gleich ist. Diese Voraussetzung wird als Homoskedastizität bezeichnet und lässt sich ebenfalls mit statistischen Tests (z.B. Goldfeld-Quandt Test) oder grafisch überprüfen. Grafisch bietet es sich an, die vorhergesagten Werte den Residuen gegenüberzustellen. Eine Verletzung der Homoskedastizität verursacht ineffiziente Varianzschätzungen. Ineffiziente Varianzschätzungen führen zu verzerrten Standardfehlern und in Folge dessen zu ungenauen Teststatistiken und Signifikanzschätzungen. In diesem Fall wird eine Regression mit robusten Standardfehlern empfohlen. Robuste Standardfehler korrigieren für Heteroskedastizität, indem der Standardfehler für jeden Datenpunkt einzeln auf Grundlage seines Residuums geschätzt wird. Es kann z.B. eine Variante des White-Schätzers herangezogen werden. Die Korrektur des Standardfehlers führt ebenfalls zu einer Korrektur von t- und p-Wert. Näheres zur Überprüfung der Homoskedastizität und weitere Korrekturverfahren werden in Hayes & Cai (2007) dargestellt. | ||
'''''Beispielstudie''''' | '''''Beispielstudie''''' | ||
| Zeile 35: | Zeile 34: | ||
In einer fiktiven Studie wurde eine negative Korrelation von -0.4 zwischen Alter und Anzahl eingeprägter Wörter in einer Gedächtnisaufgabe berechnet. Es kann davon ausgegangen werden, dass das Alter die Prädiktorvariable und die Gedächtnisleistung das Kriterium ist. Mit der Methode der kleinsten Quadrate ergibt sich für dieses Beispiel die Regressionsgleichung ''Gedächtnisleistung = 63 – 0.4 * Alter''. Der Regressionskoeffizient von -0.4 bzw. der Einfluss des Prädiktors auf das Kriterium ist bei einem Signifikanzniveau von 0.05 signifikant von 0 verschieden (p = 0.029 < 0.05). Der erwartete Wert eingeprägter Wörter verringert sich mit jedem Lebensjahr um 0.4. In Abbildung 1 wird der beschriebene Sachverhalt grafisch dargestellt. | In einer fiktiven Studie wurde eine negative Korrelation von -0.4 zwischen Alter und Anzahl eingeprägter Wörter in einer Gedächtnisaufgabe berechnet. Es kann davon ausgegangen werden, dass das Alter die Prädiktorvariable und die Gedächtnisleistung das Kriterium ist. Mit der Methode der kleinsten Quadrate ergibt sich für dieses Beispiel die Regressionsgleichung ''Gedächtnisleistung = 63 – 0.4 * Alter''. Der Regressionskoeffizient von -0.4 bzw. der Einfluss des Prädiktors auf das Kriterium ist bei einem Signifikanzniveau von 0.05 signifikant von 0 verschieden (p = 0.029 < 0.05). Der erwartete Wert eingeprägter Wörter verringert sich mit jedem Lebensjahr um 0.4. In Abbildung 1 wird der beschriebene Sachverhalt grafisch dargestellt. | ||
[[File:3_1_ELR_1.PNG|700px|Abbildung 1: Streudiagramm und Parameter der einfachen linearen Regression aus Alter und Gedächtnisleistung|link=Ausgelagerte_Bildbeschreibungen#Streudiagramm mit Regressionsgerade|Ausgelagerte Bildbeschreibung von Streudiagramm mit Regressionsgerade]] | |||
Wie auf der x-Achse erkennbar wurden in dieser Studie nur Personen zwischen 55 und 85 einbezogen. Die Regressionsgleichung ist dementsprechend nur für Personen zwischen 55 und 85 interpretierbar. Die Regressionskonstante b<sub>0</sub> = 63 entspricht dem Schätzwert ŷ für x = 0 und ist in diesem Beispiel folglich nicht interpretierbar. Um eine interpretierbare Regressionskonstante zu erhalten, bietet es sich an den Prädiktor vor der Analyse zu zentrieren, indem man von jedem Prädiktorwert den Mittelwert abzieht, sodass der Prädiktor einen Mittelwert von 0 bei gleichbleibender Standardabweichung erhält. Das ändert in der Regressionsgleichung nur den Wert der Konstante, welche nun mit 35 dem Mittelwert der Kriteriumsvariable entspricht. Bei durchschnittlichem Alter in der Stichprobe ist folglich die erwartete Anzahl eingeprägter Wörter 35. Nach der Zentrierung ist jedoch keine unmittelbare Vorhersage von Werten der Kriteriumsvariable aus Werten der Prädiktorvariable mehr möglich. Bevor die Ergebnisse der einfachen linearen Regression interpretiert werden können, müssen zunächst die Voraussetzungen überprüft werden. Sowohl der QQPlot als auch der Shapiro-Wilk-Test deuten auf normalverteilte Daten hin (Abbildung 2). Der Goldfeld-Quandt Test behält die Nullhypothese bei und auch die grafische Gegenüberstellung der Residuen mit den vorhergesagten Werten lässt nicht auf eine Verletzung der Homoskedastizität schließen (Abbildung 3). | |||
[[File:3_1_ELR_3.PNG|600px|Abbildung 3: Goldfeld-Quandt-Test und grafische Überprüfung der Homoskedastizität]] | [[File:3_1_ELR_2.PNG|600px|Abbildung 2: Q-Q-Plot und Shapiro-Wilk-Test zur Überprüfung der NV des Modellfehlers|link=Ausgelagerte_Bildbeschreibungen#Q-Q-Plot|Ausgelagerte Bildbeschreibung von Q-Q-Plot]]<span style="color: white"> kkk </span>[[File:3_1_ELR_3.PNG|600px|Abbildung 3: Goldfeld-Quandt-Test und grafische Überprüfung der Homoskedastizität|link=Ausgelagerte_Bildbeschreibungen#Goldfeld-Quandt-Test|Ausgelagerte Bildbeschreibung von Goldfeld-Quandt-Test]] | ||
Das Bestimmtheitsmaß R² ist ein globales Gütemaß und gibt an, wie viel der Varianz der Kriteriumsvariable durch die Regression mit der Prädiktorvariable erklärt werden kann. R² berechnet sich als Quotient aus den Quadratsummen der durch die Regression erklärten Varianz und der Gesamtvarianz: | Das Bestimmtheitsmaß R² ist ein globales Gütemaß und gibt an, wie viel der Varianz der Kriteriumsvariable durch die Regression mit der Prädiktorvariable erklärt werden kann. R² berechnet sich als Quotient aus den Quadratsummen der durch die Regression erklärten Varianz und der Gesamtvarianz: | ||
Die erklärte Varianz (QS(ŷ)) ergibt sich aus der Summe der quadrierten Differenzen der Schätzwerte der Regression und des arithmetischen Mittelwerts der Messwerte. Die Gesamtvarianz (QS(y)) beinhaltet zusätzlich den nicht durch die Regression erklärbaren Anteil der Varianz in Form der Residuen. Sie ergibt sich somit aus der Summe der quadrierten Abweichungen der Messwerte vom arithmetischen Mittelwert. Das Bestimmtheitsmaß kann Werte zwischen 0 und 1 annehmen und lässt sich im Falle der einfachen linearen Regression als Quadrat des Produkt-Moment Korrelationskoeffizienten r² berechnen. Im vorliegenden Beispiel ergibt sich R² = (-0.4)² = 0.16. 16 Prozent der Varianz der Gedächtnisleistung können durch das Alter aufgeklärt werden. Könnte man die Gedächtnisleistung vollständig durch das Alter erklären, ergäbe sich ein Bestimmtheitsmaß von R² = 1. In diesem Fall wären erklärte Varianz und Gesamtvarianz identisch. | [[File:3_1_ELR_Formel_6.PNG|180px|link=Ausgelagerte_Formeln#Bestimmtheitsmaß R²|Ausgelagerte Formel Bestimmtheitsmaß R²]] | ||
Die erklärte Varianz (QS(ŷ)) ergibt sich aus der Summe der quadrierten Differenzen der Schätzwerte der Regression und des arithmetischen Mittelwerts der Messwerte. Die Gesamtvarianz (QS(y)) beinhaltet zusätzlich den nicht durch die Regression erklärbaren Anteil der Varianz in Form der Residuen. Sie ergibt sich somit aus der Summe der quadrierten Abweichungen der Messwerte vom arithmetischen Mittelwert. Das Bestimmtheitsmaß kann Werte zwischen 0 und 1 annehmen und lässt sich im Falle der einfachen linearen Regression als Quadrat des Produkt-Moment Korrelationskoeffizienten r² berechnen. Im vorliegenden Beispiel ergibt sich R² = (-0.4)² = 0.16. 16 Prozent der Varianz der Gedächtnisleistung können durch das Alter aufgeklärt werden. Könnte man die Gedächtnisleistung vollständig durch das Alter erklären, ergäbe sich ein Bestimmtheitsmaß von R² = 1. In diesem Fall wären erklärte Varianz und Gesamtvarianz identisch. Die einfache lineare Regression ist eines der wichtigsten statistischen Verfahren und Grundlage für viele weitere Verfahren, die auf dem Allgemeinen Linearen Modell aufbauen. | |||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/3_1_ELR_metrisch_Link.html | ||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/3_1_ELR_metrisch_Link.html Video] wird die einfache lineare Regression näher erläutert. | ||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/ | [[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/3_1_Einfache_lineare_Regression/ | ||
|120px]] <span style="color: white"> kkk </span> In der [http://141.76.19.82:3838/mediawiki/ | |120px]] <span style="color: white"> kkk </span> In der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/3_1_Einfache_lineare_Regression/ interaktiven Simulation] können Regressionen für verschiedene Korrelationskoeffizienten berechnet und die Voraussetzungen der einfachen linearen Regression überprüft werden. | ||
Aktuelle Version vom 6. Februar 2022, 12:31 Uhr
Die einfache lineare Regression ist eine statistische Methode zur Vorhersage der Messwerte einer Variablen aus den Werten einer anderen Variablen. Anders als die Korrelationsanalyse ermöglicht die lineare Regression gerichtete Aussagen über den Einfluss einer Prädiktorvariable auf die Kriteriumsvariable. Dafür müssen a priori plausibel begründete Hypothesen darüber aufgestellt werden, welche Variable vorhersagt (Prädiktor) und welche vorhergesagt wird (Kriterium). Das Modell der einfachen linearen Regression lässt sich mithilfe der folgenden Formel darstellen:
Diese beinhaltet den Wert des Kriteriums (yi) und den Wert des Prädiktors (xi) für die Untersuchungseinheit i. Die zwei Regressionskoeffizienten in der Formel sind die Regressionskonstante (b0) und der Anstieg der Regressionsgeraden b1. Die Konstante entspricht dem Schätzwert ŷ für x = 0 und damit dem Schnittpunkt der Regressionsgeraden mit der y-Achse. Der Anstieg der Regressionsgeraden beschreibt, um wie viel der ŷ -Wert ansteigt, wenn der x-Wert um eine Einheit erhöht wird. Der zufällige Fehler bzw. das Residuum ei entspricht der Abweichung des Messwertes der Kriteriumsvariable vom vorhergesagten Schätzwert (yi - ŷi) oder grafisch veranschaulicht dem Abstand eines Messwertes von der Regressionsgerade. Bei perfekter Vorhersage durch das Modell gäbe es keine Residuen – alle Messwerte würden auf der Regressionsgerade liegen. Dieser Fall tritt in der Realität nicht ein.
Das Ziel der linearen Regression ist es, aus vorliegenden Daten ein Modell zu schätzen, welches eine optimale Vorhersage des Kriteriums aus dem Prädiktor ermöglicht. Dafür werden mit der Methode der kleinsten Quadrate diejenigen Regressionskoeffizienten geschätzt, mit denen die Summe der quadrierten Residuen minimal wird. Durch das Quadrieren der Residuen wird verhindert, dass sich positive und negative Residuen zu Null addieren. Außerdem werden Extremwerte bzw. stärker abweichende Residuen dadurch stärker berücksichtigt. Letzteres kann dazu führen, dass Ausreißer das Ergebnis der Regression stark beeinflussen. In solchen Fällen ist eine Ausreißerkorrektur, z.B. in Form einer robusten Regression, angemessen. Die robuste Regression ist resistent gegenüber Ausreißern und verwendet die Least Trimmed Squares Methode. Bei dieser Methode werden die Regressionsresiduen der Größe nach sortiert und nur die k Punkte mit den kleinsten Residuen werden von den ursprünglichen n Punkten in die Regressionsberechnung einbezogen. Dabei berechnet sich die Anzahl k mithilfe der folgenden Formel:
Mit p wird die Anzahl der zu schätzenden Koeffizienten bezeichnet, im gegebenen Fall 2 (b0 und b1). Im Fall der einfachen linearen Regression kann die Methode der kleinsten Quadrate so vereinfacht werden, dass die Regressionskoeffizienten mithilfe weniger Parameter bestimmbar sind. Die Steigung der Gerade lässt sich als Quotient aus der Kovarianz von Prädiktor und Kriterium und der Varianz des Prädiktors berechnen. Anschließend kann der Schätzwert der Regressionskonstante bestimmt werden:
Um eine lineare Regression durchführen zu können, müssen einige Voraussetzungen erfüllt werden. Zum einen muss das lineare Modell gültig sein, d.h. zwischen Prädiktor und Kriterium muss ein linearer Zusammenhang bestehen. Eine weitere Voraussetzung ist die statistische Unabhängigkeit der Modellfehler. Diese Annahme ist gewährleistet, wenn es sich um eine Zufallsziehung von Untersuchungseinheiten (z.B. Versuchspersonen) aus der Population handelt. Bei Untereinheiten innerhalb der Population oder Abhängigkeiten von zeitlichen Faktoren kann nicht von statistischer Unabhängigkeit ausgegangen werden und es müssen andere Methoden wie z.B. die Hierarchische Regression angewendet werden. Die Zufallsvariable Modellfehler hat einen Erwartungswert von Null. Entsprechend ergibt sich für die Summe der Residuen der Wert 0:
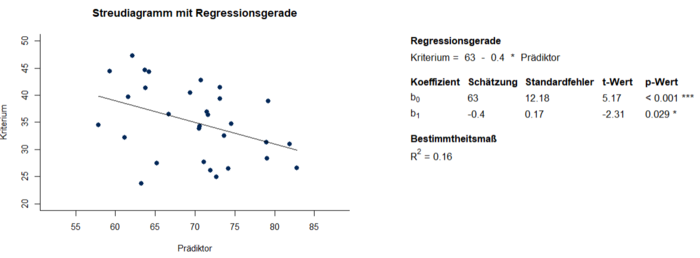
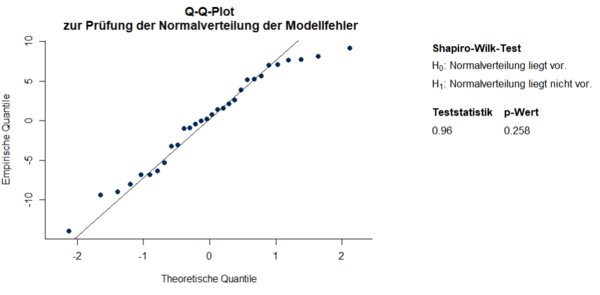
Für zuverlässige Schätzungen muss der Modellfehler normalverteilt um diesen Erwartungswert streuen. Die Normalverteilung (NV) des Modellfehlers kann mithilfe entsprechender Tests, wie des Shapiro-Wilk-Tests oder anhand grafischer Veranschaulichung durch QQ-Plots überprüft werden. Im QQ-Plot werden die empirischen Quantile der erfassten Variablen den theoretischen Quantilen der NV gegenübergestellt. Bei NV befinden sich die Punkte auf einer Geraden. Eine weitere Voraussetzung ist, dass die Varianzen der Modellfehler σ² unabhängig vom Prädiktorwert xi sind, d.h. dass die Streuung der Messwerte des Kriteriums für alle Wertebereiche des Prädiktors gleich ist. Diese Voraussetzung wird als Homoskedastizität bezeichnet und lässt sich ebenfalls mit statistischen Tests (z.B. Goldfeld-Quandt Test) oder grafisch überprüfen. Grafisch bietet es sich an, die vorhergesagten Werte den Residuen gegenüberzustellen. Eine Verletzung der Homoskedastizität verursacht ineffiziente Varianzschätzungen. Ineffiziente Varianzschätzungen führen zu verzerrten Standardfehlern und in Folge dessen zu ungenauen Teststatistiken und Signifikanzschätzungen. In diesem Fall wird eine Regression mit robusten Standardfehlern empfohlen. Robuste Standardfehler korrigieren für Heteroskedastizität, indem der Standardfehler für jeden Datenpunkt einzeln auf Grundlage seines Residuums geschätzt wird. Es kann z.B. eine Variante des White-Schätzers herangezogen werden. Die Korrektur des Standardfehlers führt ebenfalls zu einer Korrektur von t- und p-Wert. Näheres zur Überprüfung der Homoskedastizität und weitere Korrekturverfahren werden in Hayes & Cai (2007) dargestellt.
Beispielstudie
In einer fiktiven Studie wurde eine negative Korrelation von -0.4 zwischen Alter und Anzahl eingeprägter Wörter in einer Gedächtnisaufgabe berechnet. Es kann davon ausgegangen werden, dass das Alter die Prädiktorvariable und die Gedächtnisleistung das Kriterium ist. Mit der Methode der kleinsten Quadrate ergibt sich für dieses Beispiel die Regressionsgleichung Gedächtnisleistung = 63 – 0.4 * Alter. Der Regressionskoeffizient von -0.4 bzw. der Einfluss des Prädiktors auf das Kriterium ist bei einem Signifikanzniveau von 0.05 signifikant von 0 verschieden (p = 0.029 < 0.05). Der erwartete Wert eingeprägter Wörter verringert sich mit jedem Lebensjahr um 0.4. In Abbildung 1 wird der beschriebene Sachverhalt grafisch dargestellt.
Wie auf der x-Achse erkennbar wurden in dieser Studie nur Personen zwischen 55 und 85 einbezogen. Die Regressionsgleichung ist dementsprechend nur für Personen zwischen 55 und 85 interpretierbar. Die Regressionskonstante b0 = 63 entspricht dem Schätzwert ŷ für x = 0 und ist in diesem Beispiel folglich nicht interpretierbar. Um eine interpretierbare Regressionskonstante zu erhalten, bietet es sich an den Prädiktor vor der Analyse zu zentrieren, indem man von jedem Prädiktorwert den Mittelwert abzieht, sodass der Prädiktor einen Mittelwert von 0 bei gleichbleibender Standardabweichung erhält. Das ändert in der Regressionsgleichung nur den Wert der Konstante, welche nun mit 35 dem Mittelwert der Kriteriumsvariable entspricht. Bei durchschnittlichem Alter in der Stichprobe ist folglich die erwartete Anzahl eingeprägter Wörter 35. Nach der Zentrierung ist jedoch keine unmittelbare Vorhersage von Werten der Kriteriumsvariable aus Werten der Prädiktorvariable mehr möglich. Bevor die Ergebnisse der einfachen linearen Regression interpretiert werden können, müssen zunächst die Voraussetzungen überprüft werden. Sowohl der QQPlot als auch der Shapiro-Wilk-Test deuten auf normalverteilte Daten hin (Abbildung 2). Der Goldfeld-Quandt Test behält die Nullhypothese bei und auch die grafische Gegenüberstellung der Residuen mit den vorhergesagten Werten lässt nicht auf eine Verletzung der Homoskedastizität schließen (Abbildung 3).
Das Bestimmtheitsmaß R² ist ein globales Gütemaß und gibt an, wie viel der Varianz der Kriteriumsvariable durch die Regression mit der Prädiktorvariable erklärt werden kann. R² berechnet sich als Quotient aus den Quadratsummen der durch die Regression erklärten Varianz und der Gesamtvarianz:
Die erklärte Varianz (QS(ŷ)) ergibt sich aus der Summe der quadrierten Differenzen der Schätzwerte der Regression und des arithmetischen Mittelwerts der Messwerte. Die Gesamtvarianz (QS(y)) beinhaltet zusätzlich den nicht durch die Regression erklärbaren Anteil der Varianz in Form der Residuen. Sie ergibt sich somit aus der Summe der quadrierten Abweichungen der Messwerte vom arithmetischen Mittelwert. Das Bestimmtheitsmaß kann Werte zwischen 0 und 1 annehmen und lässt sich im Falle der einfachen linearen Regression als Quadrat des Produkt-Moment Korrelationskoeffizienten r² berechnen. Im vorliegenden Beispiel ergibt sich R² = (-0.4)² = 0.16. 16 Prozent der Varianz der Gedächtnisleistung können durch das Alter aufgeklärt werden. Könnte man die Gedächtnisleistung vollständig durch das Alter erklären, ergäbe sich ein Bestimmtheitsmaß von R² = 1. In diesem Fall wären erklärte Varianz und Gesamtvarianz identisch. Die einfache lineare Regression ist eines der wichtigsten statistischen Verfahren und Grundlage für viele weitere Verfahren, die auf dem Allgemeinen Linearen Modell aufbauen.
kkk Im Video wird die einfache lineare Regression näher erläutert.
kkk In der interaktiven Simulation können Regressionen für verschiedene Korrelationskoeffizienten berechnet und die Voraussetzungen der einfachen linearen Regression überprüft werden.
Weiterführende Literatur
Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.
Hayes, A. F., & Cai, L. (2007). Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior research methods, 39(4), 709-722.
Holling, H. & Gediga, G. (2010). Statistik - Deskriptive Verfahren. Göttingen: Hogrefe.
Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.1). Göttingen: Hogrefe.
Rudolf, M., & Kuhlisch, W. (2008). Biostatistik: Eine Einführung für Biowissenschaftler (Kapitel 7.4). München: Pearson Studium.