Moderierte Regression: Unterschied zwischen den Versionen
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Paul (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 23: | Zeile 23: | ||
[[File:3_8_Moderierte_Regression_2.PNG|500px|Abbildung 2: Ergebnisse der Moderatoranalyse|link=Ausgelagerte_Bildbeschreibungen# | [[File:3_8_Moderierte_Regression_2.PNG|500px|Abbildung 2: Ergebnisse der Moderatoranalyse|link=Ausgelagerte_Bildbeschreibungen#Ergebnisse_Regressionsanalyse_von_Moderierte_Regression|Ausgelagerte Bildbeschreibung von Ergebnisse Regressionsanalyse]] | ||
| Zeile 29: | Zeile 29: | ||
[[File:3_8_Moderierte_Regression_3.PNG|500px|Abbildung 3: Darstellung der moderierten Regression für der verschiedene Ausprägungen der Moderatorvariable (Einkommen)]] | [[File:3_8_Moderierte_Regression_3.PNG|500px|Abbildung 3: Darstellung der moderierten Regression für der verschiedene Ausprägungen der Moderatorvariable (Einkommen)|link=Ausgelagerte_Bildbeschreibungen#Bedingte Regression|Ausgelagerte Bildbeschreibung von Bedingte Regression]] | ||
Aktuelle Version vom 6. Februar 2022, 13:44 Uhr
Moderierte Regressionen ermöglichen es, im Rahmen von multiplen linearen Regressionen zu überprüfen, ob die Einflussstärke eines Prädiktors auf das Kriterium abhängig von der Ausprägung eines weiteren Prädiktors ist.
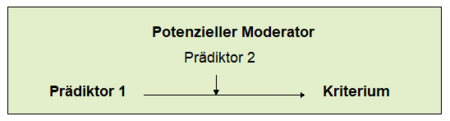
Die multiple lineare Regression stellt das Kriterium als lineare Funktion der einzelnen Prädiktoren dar. Eine rein additive Verknüpfung der Prädiktoren ist zur Erklärung des Kriteriums jedoch nicht immer ausreichend. So werden zum Beispiel Einflüsse von Prädiktoren auf das Kriterium häufig von anderen Prädiktoren moderiert. In Abbildung 1 wird das Prinzip einer Moderation schematisch veranschaulicht. Die Stärke des gerichteten Einflusses von Prädiktor 1 auf das Kriterium unterscheidet sich für verschiedene Ausprägungen im Prädiktor 2.
Um Moderatoreffekte statistisch zu überprüfen, können in das Modell einer multiplen lineare Regression zusätzlich Interaktionseffekte zwischen zwei oder mehr Variablen aufgenommen werden. Eine moderierte Regression mit zwei Prädiktorvariablen und einem Interaktionseffekt lässt sich durch die folgende Formel darstellen:
Die Interaktion stellt in dem Modell das Produkt der Werte der beiden Variablen X1 und X2 dar. Der Regressionskoeffizient b3 der Interaktion wird, wie die anderen Regressionskoeffizienten, aus den Daten geschätzt und kann mit einem Signifikanztest gegen die Nullhypothese getestet werden. Welcher der beiden Prädiktoren als Moderator in das Modell einfließt, ist nicht anhand des Interaktionsterms erkennbar, sondern muss auf Basis von inhaltlichen Überlegungen vorher festgelegt werden.
Beispiel
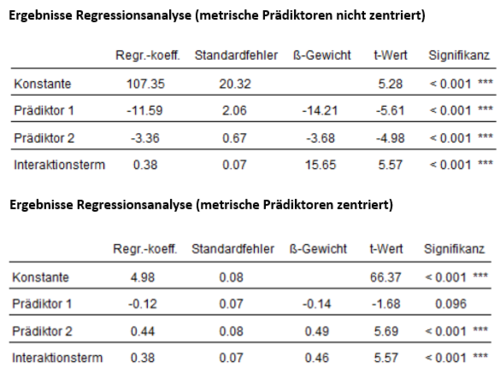
In einer fiktiven Studie soll überprüft werden, ob sich das Einkommen moderierend auf den Zusammenhang zwischen Alter und Lebenszufriedenheit auswirkt. Dafür soll ein Modell analog zu Abbildung 1 überprüft werden, wobei das Alter hier Prädiktor 1, das monatliche Einkommen Prädiktor 2 bzw. den potenziellen Moderator und die Lebenszufriedenheit das Kriterium darstellt. Um den Moderatoreffekt zu überprüfen, wird in einer multiplen linearen Regression zusätzlich zu den beiden Prädiktoren deren Interaktionsterm in das Modell aufgenommen. Die Ergebnisse der berechneten Regressionsanalyse werden in Abbildung 2 dargestellt.
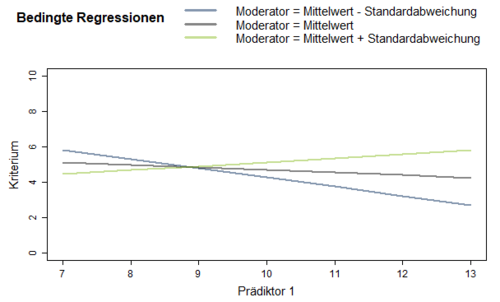
Sowohl die Regressionskoeffizienten der beiden Prädiktoren als auch der des Interaktionsterms sind signifikant von 0 verschieden (p < 0.001). Der Regressionskoeffizient des Interaktionsterms (b3= 0.38) beschreibt, um wie viele Einheiten der Regressionskoeffizient des Alters ansteigt, wenn sich der Wert der Moderatorvariable, hier des Einkommens, um eine Einheit erhöht. Eine Einheit bedeutet hier 100 Euro Nettoverdienst pro Monat. In diesem Beispiel steigt also der Einfluss des Alters auf die Lebenszufriedenheit für ein höheres Einkommen um 0.38 Einheiten pro 100 Euro. Die Signifikanzprüfung des Koeffizienten b3 ist entscheidend dafür, ob ein Moderatoreffekt der Variablen Einkommen nachgewiesen werden kann. Im Beispiel ist das der Fall (p < .001; siehe Abbildung 2). In Abbildung 3 wird der beschriebene Moderatoreffekt anhand verschiedener Regressionsgeraden veranschaulicht.
Bei mittlerem Einkommen ergibt sich kein erkennbarer Zusammenhang zwischen Alter und Lebenszufriedenheit (= graue mittlere Regressionsgerade). Bei Moderatorwerten, die dem Mittelwert ± einer Standardabweichung entsprechen, ergeben sich entsprechend dem Interaktionsterm für ein höheres Einkommen positive und für ein geringeres Einkommen negative Zusammenhänge zwischen Alter und Lebenszufriedenheit.
Die in der Regressionsanalyse berechneten Regressionskoeffizienten der einzelnen Prädiktoren entsprechen dem Zusammenhang des jeweiligen Prädiktors mit dem Kriterium, wenn alle anderen Prädiktoren den Wert 0 haben. Für das Alter ergibt sich z.B. ein stark negativer Einfluss auf die Lebenszufriedenheit, wenn das Einkommen 0 Euro beträgt (b1 = -11.59, p < 0.001). Da man davon ausgehen kann, dass ein Einkommen von 0 Euro in einer Stichprobe Erwerbstätiger nicht auftritt, ist dieser Wert nicht interpretierbar. Um diesen besser interpretierbar zu machen, bietet es sich an, die Prädiktorvariablen vorher zu zentrieren. Das Vorgehen der Zentrierung wird im Text zur einfachen linearen Regression beschrieben. Nach der Zentrierung entspricht das Regressionsgewicht eines Prädiktors dessen Einfluss auf das Kriterium, wenn alle anderen Prädiktoren eine durchschnittliche Ausprägung aufweisen. Dabei wird sowohl die Höhe als auch die statistische Signifikanz der Regressionskoeffizienten durch die Zentrierung beeinflusst. So verringert sich im vorliegenden Beispiel der signifikante Regressionskoeffizient des Alters durch die Zentrierung auf b1 = -0.12 und ist somit nach der Zentrierung nicht mehr signifikant von 0 verschieden (p = 0.096, vgl. Abbildung 2). Bei durchschnittlicher Ausprägung des Einkommens hat das Alter also keinen signifikanten Einfluss auf die Lebenszufriedenheit (vgl. Abbildung 3). Das Ergebnis bezüglich des Regressionskoeffizienten b3 des Interaktionsterms und damit die Aussage zum Moderatoreffekt werden durch die Zentrierung nicht beeinflusst. Zusätzlich zur Veränderung der Regressionskoeffizienten werden außerdem die Korrelationen der Prädiktoren mit dem Interaktionsterm reduziert. Die Korrelation zwischen Prädiktoren wird durch die Zentrierung hingegen nicht beeinflusst und kann weiterhin als Indikator für Multikollinearität verwendet werden. Im vorliegenden Beispiel wird z.B. die sehr hohe Korrelation zwischen dem Alter und dem Interaktionsterm Alter * Einkommen (r = 0.97) nach der Zentrierung 0. Die schwache Korrelation der beiden Prädiktoren (r = 0.26) bleibt nach der Zentrierung hingegen unverändert.
kkk Im Video wird die moderierte Regression näher erläutert.
kkk In der interaktiven Simulation können Regressionen mit unterschiedlich starken Moderatoreffekten grafisch nachvollzogen werden.
Weiterführende Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden. Weinheim: Beltz.
Rudolf, M. & Buse, J. (2020). Multivariate Verfahren. Eine praxisorientierte Einführung mit Anwendungsbeispielen (3. Aufl., Kapitel 2.2.4). Göttingen: Hogrefe. .