Standardfehler der Regressionskoeffizienten: Unterschied zwischen den Versionen
Wehner (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{Nav|Navigation|Statistik_MV|Hauptseite}}“) |
Elisa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Nav|Navigation|Statistik_MV|Hauptseite}} | {{Nav|Navigation|Statistik_MV|Hauptseite}} | ||
Der Standardfehler gibt in der linearen Regression die Genauigkeit der Schätzung der Regressionskoeffizienten an und wird unter anderem für die Berechnung von Signifikanzen benötigt. Unter erfüllten Annahmen der [[Einfache lineare Regression bei metrischem Prädiktor|linearen Regression]] ist die Stichprobenverteilung eines Regressionskoeffizienten b normalverteilt. Die Standardabweichung dieser Verteilung entspricht dem Standardfehler des Regressionskoeffizienten s<sub>b</sub> (Formeln siehe Bortz und Schuster, 2016). | |||
'''''Beispiel 1''''' | |||
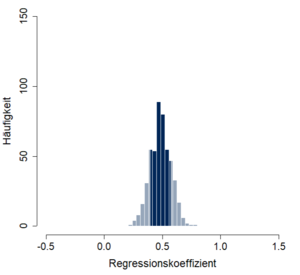
Aus einer Grundgesamtheit, in der Prädiktor und Kriterium durchschnittlich mit r = 0.5 korrelieren, werden 500 Stichproben gezogen. Für jede Stichprobe werden die Parameter einer einfachen linearen Regression geschätzt. Die ermittelten Regressionskoeffizienten streuen um den Mittelwert b = 0.5. Die Standardabweichung dieser Verteilung bzw. der Standardfehler des Regressionskoeffizienten entspricht s<sub>b</sub> = 0.1. In Abbildung 1 wird der beschriebene Sachverhalt dargestellt. | |||
[[File:3_7_MLR_1.PNG|300px|Abbildung 1: Häufigkeitsverteilung des Regressionskoeffizienten einer einfachen linearen Regression|link=Ausgelagerte_Bildbeschreibungen#Bespiel Standardfehler|Ausgelagerte Bildbeschreibung von Bespiel Standardfehler]] | |||
Will man den Standardfehler der Regressionskoeffizienten bei der [[Grundlagen der multiplen linearen Regression|multiplen linearen Regression]] schätzen, müssen Abhängigkeiten mit anderen Prädiktoren berücksichtigt werden (Formeln siehe Bortz und Schuster, 2016). Ein hoher Standardfehler kann dabei ein Hinweis für das Vorliegen von Multikollinearität sein. | |||
'''''Beispiel 2''''' | |||
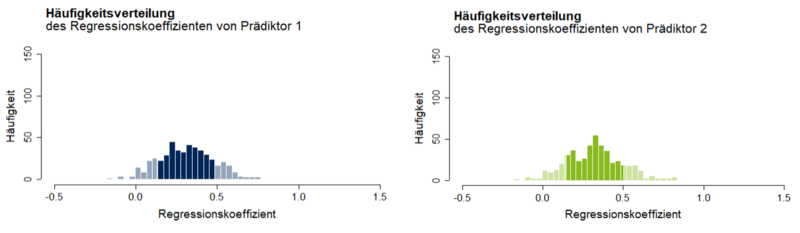
Aus einer Grundgesamtheit, in der zwei Prädiktoren jeweils zu r = 0.6 mit dem Kriterium und untereinander zu r = 0.9 korrelieren, wird die Verteilung der beiden Regressionskoeffizienten simuliert. Die hohe Korrelation beider Prädiktoren führt bei der Schätzung der Regressionskoeffizienten in einigen Stichproben dazu, dass ein Prädiktor die relevanten Varianzanteile des zweiten übernimmt, sodass dessen Regressionskoeffizient – trotz hoher Korrelation mit dem Kriterium – nahe null liegt. In anderen Zufallsziehungen ist es genau andersherum. Die daraus resultierenden Verteilungen der Regressionskoeffizienten streuen bei großen Standardfehlern (s<sub>b<sub>1</sub></sub> = 0.23; s<sub>b<sub>2</sub></sub> = 0.22) um Mittelwerte, die geringer sind, als es die Korrelation von r = 0.6 vermuten lässt (Abbildung 2). Bei zwei unkorrelierten Prädiktoren ergäben sich größere Regressionskoeffizienten und schmalere Häufigkeitsverteilungen. | |||
[[File:3_7_MLR_2.PNG|800px|Abbildung 2: Häufigkeitsverteilungen zweier hochkorrelierter Regressionskoeffizienten in einer multiplen linearen Regression|link=Ausgelagerte_Bildbeschreibungen|Häufigkeitsverteilungen_zweier_Regressionskoeffizienten|Ausgelagerte Bildbeschreibung von Häufigkeitsverteilungen zweier Regressionskoeffizienten]] | |||
Der Standardfehler wird in der Regressionsanalyse für den Signifikanztest von Regressionskoeffizienten benötigt. Die zur Bestimmung des p-Wertes relevanten t-Werte ergeben sich als Quotient aus Regressionskoeffizient und Standardfehler. Je höher der Standardfehler ist, desto niedriger ist dementsprechend der t-Wert und desto unsicherer der Einfluss des Prädiktors auf das Kriterium. So ist der Regressionskoeffizient aus Abbildung 1 signifikant von 0 verschieden, die beiden Regressionskoeffizienten aus Abbildung 2 jedoch nicht. | |||
[[Datei:Videolink_neu.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/3_7_MLR_Standardfehler_Link.html | |||
|120px]] <span style="color: white"> kkk </span> Im [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Videolinks/3_7_MLR_Standardfehler_Link.html Video] wird der Standardfehler des Regressionskoeffizienten näher erläutert. | |||
[[Datei:Simulationslink_neu2.PNG|link=http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/3_7_MLR_Standardfehler_Multikollinearitaet/ | |||
|120px]] <span style="color: white"> kkk </span> Die Entstehung des Standardfehlers der Regressionskoeffizienten lässt sich in der [http://141.76.19.82:3838/mediawiki/MUVE_STAT/Apps/3_7_MLR_Standardfehler_Multikollinearitaet/ interaktiven Simulation] grafisch nachvollziehen. | |||
'''''Weiterführende Literatur''''' | |||
Bortz, J., & Schuster, C. (2016). ''Statistik für Human- und Sozialwissenschaftler''. Berlin: Springer. | |||
Aktuelle Version vom 21. März 2022, 09:01 Uhr
Der Standardfehler gibt in der linearen Regression die Genauigkeit der Schätzung der Regressionskoeffizienten an und wird unter anderem für die Berechnung von Signifikanzen benötigt. Unter erfüllten Annahmen der linearen Regression ist die Stichprobenverteilung eines Regressionskoeffizienten b normalverteilt. Die Standardabweichung dieser Verteilung entspricht dem Standardfehler des Regressionskoeffizienten sb (Formeln siehe Bortz und Schuster, 2016).
Beispiel 1
Aus einer Grundgesamtheit, in der Prädiktor und Kriterium durchschnittlich mit r = 0.5 korrelieren, werden 500 Stichproben gezogen. Für jede Stichprobe werden die Parameter einer einfachen linearen Regression geschätzt. Die ermittelten Regressionskoeffizienten streuen um den Mittelwert b = 0.5. Die Standardabweichung dieser Verteilung bzw. der Standardfehler des Regressionskoeffizienten entspricht sb = 0.1. In Abbildung 1 wird der beschriebene Sachverhalt dargestellt.
Will man den Standardfehler der Regressionskoeffizienten bei der multiplen linearen Regression schätzen, müssen Abhängigkeiten mit anderen Prädiktoren berücksichtigt werden (Formeln siehe Bortz und Schuster, 2016). Ein hoher Standardfehler kann dabei ein Hinweis für das Vorliegen von Multikollinearität sein.
Beispiel 2
Aus einer Grundgesamtheit, in der zwei Prädiktoren jeweils zu r = 0.6 mit dem Kriterium und untereinander zu r = 0.9 korrelieren, wird die Verteilung der beiden Regressionskoeffizienten simuliert. Die hohe Korrelation beider Prädiktoren führt bei der Schätzung der Regressionskoeffizienten in einigen Stichproben dazu, dass ein Prädiktor die relevanten Varianzanteile des zweiten übernimmt, sodass dessen Regressionskoeffizient – trotz hoher Korrelation mit dem Kriterium – nahe null liegt. In anderen Zufallsziehungen ist es genau andersherum. Die daraus resultierenden Verteilungen der Regressionskoeffizienten streuen bei großen Standardfehlern (sb1 = 0.23; sb2 = 0.22) um Mittelwerte, die geringer sind, als es die Korrelation von r = 0.6 vermuten lässt (Abbildung 2). Bei zwei unkorrelierten Prädiktoren ergäben sich größere Regressionskoeffizienten und schmalere Häufigkeitsverteilungen.
Der Standardfehler wird in der Regressionsanalyse für den Signifikanztest von Regressionskoeffizienten benötigt. Die zur Bestimmung des p-Wertes relevanten t-Werte ergeben sich als Quotient aus Regressionskoeffizient und Standardfehler. Je höher der Standardfehler ist, desto niedriger ist dementsprechend der t-Wert und desto unsicherer der Einfluss des Prädiktors auf das Kriterium. So ist der Regressionskoeffizient aus Abbildung 1 signifikant von 0 verschieden, die beiden Regressionskoeffizienten aus Abbildung 2 jedoch nicht.
kkk Im Video wird der Standardfehler des Regressionskoeffizienten näher erläutert.
kkk Die Entstehung des Standardfehlers der Regressionskoeffizienten lässt sich in der interaktiven Simulation grafisch nachvollziehen.
Weiterführende Literatur
Bortz, J., & Schuster, C. (2016). Statistik für Human- und Sozialwissenschaftler. Berlin: Springer.